Как называется подкова в геометрии
Что означает знак дуги в геометрии – как обозначается дуга в геометрии
⌒ — Дуга (U+2312) — Таблица символов Юникода®
Начертание символа «Дуга» в разных шрифтах
Описание символа
Дуга. Разнообразные технические символы.
Связанные символы
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 8C 92 | 226 140 146 | 14847122 | 11100010 10001100 10010010 |
| UTF-16BE | 23 12 | 35 18 | 8978 | 00100011 00010010 |
| UTF-16LE | 12 23 | 18 35 | 4643 | 00010010 00100011 |
| UTF-32BE | 00 00 23 12 | 0 0 35 18 | 8978 | 00000000 00000000 00100011 00010010 |
| UTF-32LE | 12 23 00 00 | 18 35 0 0 | 304283648 | 00010010 00100011 00000000 00000000 |
Дуга (геометрия) — это… Что такое Дуга (геометрия)?
Дуга — связное подмножество окружности.
Свойства
*Длина дуги L радиуса R с центральным углом alpha, измеренным в радианах, вычисляется по формуле: L=Ralpha
Wikimedia Foundation. 2010.
Смотреть что такое «Дуга (геометрия)» в других словарях:
Дуга — Дуга: В математике Дуга (геометрия) участок кривой между двумя её точками. Дуга окружности кривая линия, лежащая на окружности и ограниченная двумя точками. Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
Геометрия — (γήμετρώ земля, μετρώ мерю). Понятия о пространстве, положении и форме принадлежат к числу первоначальных, с которыми человек был знаком уже в глубокой древности. Первые шаги в Г. были сделаны египтянами и халдеями. В Греции Г. была введена… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
АФФИННАЯ ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, изучающий дифференциально геометрич. свойства кривых и поверхностей, сохраняющиеся при преобразованиях аффинной группы или ее подгрупп. Наиболее полно изучена дифференциальная геометрия эквиаффинного пространства. В эквиаффинной … Математическая энциклопедия
РИМАНОВА ГЕОМЕТРИЯ — теория риманова пространства. Р и м а н о в ы м п р о с т р а н с т в о м наз. n мерное связное дифференцируемое многообразие М п, на к ром задано дифференцируемое поле ковариантного, симметрического и положительно определенного тензора gранга 2 … Математическая энциклопедия
Сферическая геометрия — математическая дисциплина, изучающая геометрические образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрические образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, даёт в сечении… … Большая советская энциклопедия
Хорда (геометрия) — У этого термина существуют и другие значения, см. Хорда. 1 секущая, 2 хорда … Википедия
СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ — математич. дисциплина, изучающая геометрич. образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрич. образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, дает в сечении нек рую окружность; если секущая… … Математическая энциклопедия
ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ — геодезиче ская, геометрическое понятие, обобщающее понятие прямой (или отрезка прямой) евклидовой геометрии на случай пространств более общего вида. Определения Г. л. в различных пространствах зависят от того, какая из структур (метрика, линейный … Математическая энциклопедия
Декарт Рене — (Descartes) (латинизир. Картезий; Cartesius) (1596 1650), французский философ, математик, физик и физиолог. С 1629 в Нидерландах. Заложил основы аналитической геометрии, дал понятия переменной величины и функции, ввёл многие алгебраические… … Энциклопедический словарь
Жорданова кривая — Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия
Дуга окружности. Полуокружность определение. Длина дуги окружности. Угол и дуга окружности
Дуга окружности
Что такое дуга окружности?
Дугу окружности принято обозначать тремя точками: две точки – это концы дуги и одна произвольная промежуточная точка. Пример дуги:
На картинке представлены две дуги: ACB и ADB.
Полуокружность определение
Полуокружностью называют дугу окружности, если отрезок, соединяющий её концы, в нашем случае AB, есть диаметр окружности.
На картинке ACB – полуокружность:
Градусная мера дуги окружности
Рассмотрим три случая.
Первый случай
Градусной мерой дуги ACB является градусная мера центрального угла AOB:
Второй случай
Третий случай
А чему равна сумма градусных мер дуг ADB и ACB?
Градусная мера дуги ADB равна 90 0 по условию.
Основные геометрические фигуры
Основные понятия
Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.
Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.
Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.
Обучение на курсах по математике поможет быстрее разобраться в видах и свойствах геометрических фигур.
Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской P.
Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Если все точки фигуры принадлежат одной плоскости, значит она является плоской.
Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.
Примеры объемных геометрических фигур:
Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые.
Узнать площадь прямоугольника помогут следующие формулы:
Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.
Периметр прямоугольника — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Квадрат
Квадрат — это тот же прямоугольник, у которого все стороны равны.
Найти площадь квадрата легко:
Периметр квадрата — это длина стороны, умноженная на четыре.
P = 4 × a, где a — длина стороны.
Трапеция
Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.
Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.
Как найти площадь трапеции:
S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.
Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.
P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны
Ромб — это параллелограмм с равными сторонами.
Общие формулы расчета площади фигур:
Периметр ромба — это произведение длины стороны на четыре.
P = 4 × a, где a — длина стороны.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Треугольник
Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.
Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.
S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.
Основание может быть расположено иначе, например так:
При тупом угле высоту можно отразить на продолжение основания:
При прямом угле основанием и высотой будут его катеты:
S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.
S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.
P = 3 × a, где a — длина стороны.
Круг — это это часть плоскости, которая лежит внутри окружности.
Окружность — это граница круга.
Радиус окружности — это расстояние от центра окружности до любой точки на ней.
Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.
Формулы площади круга:
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Металлоискатели в России / Только белая техника!
КОМПАНИЯ
УСЛУГИ
РЕСУРСЫ И СЕРВИСЫ
Подковы тоже бывают разные
Возможно ли среди подков найти действительно стоящую, которую коллекционеры оторвут с руками? Вероятно, возможно, если это будет подкова из золота.
Но мы с вами поговорим о том, что встречается на копе и вообще о разных интересных подковах, кроме, конечно, золотых.
Если катко, у лошадей на ногах – копыта. По структуре они как наши ногти, только, понятное дело, куда массивнее и тверже. От хождения по твердому грунту, дорожному покрытию и по настилу конюшен копыта снашиваются, лошади начинают хромать. Чтобы этого избежать, лошадей подковывают. Поскольку лошадь в Евразии была основным транспортом и тягловой силой на протяжении тысячелетий, подков у нас в земле должно накопиться немеряно. Так оно и есть!
Поверья
В связи с тем, что лошадь символом достатка, возможно и появилась вера в счастливые качества лошадиной подковы. Вера в подкову широко распространена и в России, считается, что найти старое железо, особенно подкову – приносит счастье, а найденная подкова, прибитая к порогу торгового заведения, приносит удачу в торговле. В русских деревнях, а сейчас – и в городских домах и квартирах можно увидеть подкову, прибитую над дверью.
Кроме русских, в счастливые свойства подковы верят многие народы по всему миру: англичане, французы, турки, евреи и другие. Даже те, кто возмущается, когда их называют суеверными. Характерным примером можно считать случай с академиком Павловым, над дверью которого была прибита подкова. На вопрос, верит ли он в то, что подкова приносит удачу, он ответил: «Конечно, не верю»! А потом добавил: «Но это работает, даже когда не веришь».
История подковы
Как принято считать, метод подковывания лошадей изобрели галлы или кельты приблизительно в IV–III вв. до н. э. Затем полезное нововведение переняли римляне. Они использовали для защиты подошвы копыта металлические пластинки овальной формы, с крючками, дужками, ушками или кольцами для укрепления пластинки на копыте ремнем. Также имперцы поняли, что не только лошади нуждаются в таких приспособлениях. В общем, пластинки для лошадей назывались гиппосандалиями, для мулов — мулосандалиями, для быков — бососандалиями.
И здесь мы на секундочку вернемся к подковам из драгоценных металлов. Роскошь Древнего Рима, думаю, всем известна. Судя по историческим хроникам, у мулов Помпеи, супруги Нерона, были золотые подошвы, а лошади Нерона, запряженные в колесницы, носили серебряные подошвы. Наверное, откопать такое чудо было бы очень приятно.
Вернемся к нашим баранам, а вернее, лошадям и их подковам на Руси. Подробности и практический материал взят из книги А.Н. Кирпичникова «Археология СССР». Там, кстати, очень много полезной информации – и по деталям конской упряжи, и по оружию, и по инфм артефактам прежних времен.
Подковывать копыта и крепить подковы специальными гвоздями у нас научились не ранее XI века. Есть некоторые свидетельства об этом в исторических источниках. Например, в Радзивилловской летописи (начало XIII в.) легендарный конь князя Олега изображен подкованным.
Однако на Руси было сильным влияние степняков, которые оставляли копыта лошадей в естественном состоянии. И у русской конницы до XVI вследствие этого не было подков. Так что ранние, домонгольские подковы, принадлежат торговым, тягловым лошадям.
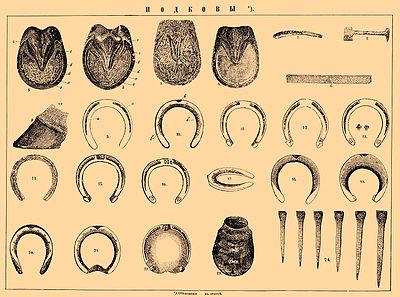
Известны две типологические формы домонгольских «транспортных» подков. Они показаны на рисунке ниже.
Дальнейшая трансформация подков заключалась в том, что они становились крупнее, края перестали быть волнистыми, а на нижней поверхности появился желобок для гвоздей.
Рис. 1. Ледоходный шип XI-XV вв.
Рис. 2. Подкова. XI-XVII вв.
Рис. 3. Подкова. XV-XVII вв. Такой подковой ковались по большей части гужевые лошади: у нее выражена функция предохранения копыта лошади.
Рис. 4. Подкова. XVI-XVII вв. Она уже защищала все копыто лошади, что сближало ее с общеевропейской традицией.
Рис. 5. Подкова. XVI-XVII вв. Относится к старогерманскому (шведскому) типу подков. Отличается заостренными задними шипами.
Рис. 6. Подкова. XVI-XVII вв. Относится к цетральноевропейскому типу подков. Ее, как европейскую, выдает отсутствие шипов, которое не свойственно российской традиции. Роль шипов в этом случае играет проделанная по всему контуру гвоздевая дорожка
Рис. 7, 8. В России подковы такого типа появились в XVI в. Для подков этого типа в XVI-XVII вв. характерны почти равное отношение ширины к длине, ширина металла в зацепной части 4-6 см, толщина 0,4-0,6 см. Тенденции развития привели к увеличению длины по отношению к ширине на 1-2 см, уменьшению ширины металла в зацепной части до 2-3 см и увеличению толщины до 0,7-1 см.
Рис. 9. Подкова с широкой верхней частью. XVI-XVII вв.
Рис. 10. Подкова. XIX-XX вв. Относится к варшавскому типу подков. Применялась для подковывания лошадей, выполнявших гужевые работы. Занесена в период Отечественной войны 1812 г. После присоединения Польши к России применялась повсеместно.
Рис. 11. Подкова. XIX-XX вв. Для ковки скаковых лошадей.
С 1945 г. заводское производство подков в России прекратилось, и с тех пор их куют вручную по старым добрым технологиям.
Рис. 14. Толстая дорожная подкова с десятью гвоздевыми отверстиями и четырьмя от винтовых шипов. Подобными ковались лошади артиллерийских частей Вермахта.
Рис. 15 Подкова в виде трехчетвертного овала с шестью гвоздевыми отверстиями. Желобок, соединяющий отверстия для подковных гвоздей, у нее был выражен слабо, шипы сформированы за счет загиба пластины. Подобные подковы характерны для казачьих и польско-литовских войск 16-17 веков.
Современность
Формы и конструкции подков в наше время бывают разными, можно выделить несколько разновидностей.
Что делать с найденными подковами?
Каждый копарь, находивший подкову, наверняка задавал себе этот вопрос. А уж если повезло и было откопано несколько конских аксессуаров, то вопрос становился особенно актуальным. Раньше, на заре приборного поиска, было принято развешивать подковы по веткам деревьев вблизи от найденного места – вроде как на удачу.
Сегодня народ пошел осторожный и засвечивать места копа не хочет. Поэтому каждый решает сам за себя, что делать с найденной подковой. Основных варианта, как водится, два: оставить на поле или взять собой. Во втором случае подкове нужно будет придумать применение.
Применение подков:
Подарочные панно из мастерской старинных подарков. Стоят по 8000 рублей!
И еще много чего, что фантазия подскажет. Может быть, именно вам подковы принесут море удачи, и приманят и золото, и серебро?
Что означает знак подковы в геометрии?
Что означает знак дуги в геометрии?
Дуга — Дуга: В математике Дуга (геометрия) участок кривой между двумя её точками. Дуга окружности кривая линия, лежащая на окружности и ограниченная двумя точками.
Что значит знак подкова?
Подкова (фр. Fer à cheval) — символ удачи и счастья. У разных европейских народов подкова — символ удачи. Бытовало поверие, что дьявол всегда ходит кругами, но дойдя до конца подковы (разорванного круга), он вынужден повернуть обратно.
Что значит перевернутая подкова?
Повернутая концами вверх и изображенная в виде месяца подкова олицетворяет Луну и ее богинь, принимая символизм рогов власти и защиты. Может также означать йони. Апотропаична и приносит удачу. Перевернутая подкова силы удачи не имеет.
Как в геометрии обозначается пересечение?
Как обозначается пересечение прямых
В тексте пересечение прямых обозначают символом ∩. Информацию на рисунке выше можно записать следующим образом: b ∩ c — прямые b и с пересекаются; a ∩ c — прямые a и с пересекаются.
Что такое градусная мера дуги окружности?
Градусная мера дуги — это градусная мера соответствующего ей центрального угла. NMB = 360° — ∠NOB = 360° — 135° = 225°.
Как в геометрии обозначается знак принадлежности?
Знак «принадлежит» в геометрии обозначается так — ∈.
Как правильно вешать подкову?
При входе в дом со стороны улицы подкова вешается рожками вниз. По поверью злой дух от входящего попадает в чашу подковы, но выбраться не может, так как стремится вверх, а наверху — железо. Другое поверие говорит, что если подкова прибита рожками вниз, то неудача стекает по подкове и не накапливается.
Как вешать подкову на богатство?
Это своего рода магнит, способный привлечь и удержать всевозможные блага. Знатоки фэн-шуй тоже склоняются к этому варианту, рассматривая подкову как накопитель энергии и источник семейного благополучия. Многие предпочитают вешать или ставить подкову именно в таком положении.
Почему подкова считается символом удачи?
Что означает перевернутая U в математике?
— символ объединения множеств.
Что такое с в геометрии?
С — длина окружности в геометрии.
Как отмечается в геометрии перпендикуляр?
Перпендикулярность прямых обозначается знаком _|_. На чертежах 53 и 54 АВ_|_DС и DС _|_ АВ. Каждая из этих прямых называется перпендикуляром к другой. АВ — перпендикуляр к СD, и СD — перпендикуляр к АВ.
Как называется знак %0?
Как обозначается плоскость в геометрии?
Подкова
Подкова — приспособление для предохранения копыт лошади. Была изобретена в III веке в Германии.
Содержание
Предназначение
При работе лошади на твёрдом грунте роговые части копыта быстро изнашиваются. При повреждении копыта лошадь испытывает болезненные ощущения, начинает хромать, или вообще отказывается ступать на больную ногу. Ковка позволяет предохранить копыта от износа и защитить их от травмирующих ударов о твёрдый грунт. В зимнее время подковы, снабжённые шипами, улучшают сцепление копыта с грунтом и предотвращают скольжение. Специальные типы подков (ортопедические подковы) применяются при лечении различных заболеваний конечностей лошади. Крупный рогатый скот тоже нуждается в ортопедических подковах.
История
Первые приспособления сплетались в виде чулка или башмака из лыка, тростника, кожи, растительных волокон. Укреплялись над венчиком копыта под щёткой верёвками или ремнями. Эти башмаки были непрочны, укрепление их верёвками или ремнями вызывало дерматиты. Подошвенные поверхности копыт рабочего скота покрывали смолой.
Римляне употребляли для защиты подошвенной поверхности копыта металлические пластинки, большей частью овальной формы, с крючками, дужками, ушками или кольцами, для укрепления пластинки на копыте верёвкой или ремнём. Такие пластинки для лошадей назывались гиппосандалиями, для мулов — мулосандалиями, для быков — бососандалиями.
В средние века научились крепить металлические подковы специальными гвоздями — ухналями.
В России ковочное дело начало развиваться на государственном уровне после Указа Петра I 1715 года: « В Москве и губерниях сыскать кузнецов добрых, взять во всякую губернию по два человека и велеть им учить кузнечному делу русских…». В 1732 году в селе Хорошево под Москвой была открыта первая в Европе коновальная школа.
Устройство подковы
Стандартная подкова выделывается из мягкой низкоуглеродистой стали. Современные подковы достаточно пластичны, и легко поддаются подгонке на наковальне как в горячем, так и в холодном состоянии. Ширина полотна подковы среднего размера — около 22 мм, толщина — 8 мм. Верхняя, подошвенная, поверхность полотна подковы почти всегда плоская, нижняя — может быть как плоской, так и другого профиля, например, полукруглой или имеющей скосы — контрбухтовку.
В передней (зацепной) части подковы обычно имеется направленный вверх отворот — металлический лепесток, способствующий более прочной фиксации подковы на копыте. Подковы для задних копыт часто снабжены двумя отворотами, расположенными по бокам в передней её трети. На нижней поверхности каждой из ветвей подковы пробита гвоздевая дорожка — желобок, в котором утапливаются головки подковных гвоздей. На зимних рысачьих подковах гвоздевая дорожка обычно отсутствует. В дорожке располагаются гвоздевые отверстия, обычно по 4 на каждой ветви. В пяточной части подковы часто имеются резьбовые отверстия для вкручивания подковных шипов. Зацепный пластинчатый шип (захват) на современных подковах встречается редко.
Подковы для передних копыт имеют округлую форму, для задних копыт — несколько более вытянутую, что соответствует естественной форме передних и задних копыт. Подковы многих производителей имеют различия между правой и левой, что отмечается клеймением на подкове: клеймо ставится на внешней ветви. В таком случае внешняя ветвь подковы делается немного длиннее внутренней и несколько круче изогнута.
Подковы специального назначения, в том числе ортопедические, предназначенные для компенсации тех или иных недостатков копыт или лечения болезней конечностей лошади, могут иметь самую разнообразную, в том числе довольно неожиданную, форму.
Типы подков
Стандарты
Стандартные подковы изготавливают заводским способом по ГОСТу 5408—77. В соответствии с размерами копыт по стандарту выпускаются подковы 13 размеров.
Подковные гвозди вырабатываются машинным способом. Существует более десяти типов подковных гвоздей, каждый из типов имеет несколько, обычно шесть, основных размеров.
Российская и зарубежная нумерация размеров подков существенно отличается, что часто приводит к путанице.