Тоже что и шестиугольник
Шестиугольник, виды, свойства и формулы
Шестиугольник, виды, свойства и формулы.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник, выпуклый и невыпуклый шестиугольник:
Шестиугольник – это многоугольник с шестью углами.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый шестиугольник
Рис. 2. Невыпуклый шестиугольник
Сумма внутренних углов любого выпуклого шестиугольника равна 720°.
.
Правильный шестиугольник (понятие и определение):
Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.
Рис. 3. Правильный шестиугольник
Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.
Правильный шестиугольник можно построить с помощью циркуля и линейки.
Свойства правильного шестиугольника:
1. Все стороны правильного шестиугольника равны между собой.
2. Все углы равны между собой и составляют 120°.
Рис. 4. Правильный шестиугольник
3. Сумма внутренних углов любого правильного шестиугольника равна 720°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.
Рис. 5. Правильный шестиугольник
5. Количество диагоналей правильного шестиугольника равно 9.
Рис. 6. Правильный шестиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный шестиугольник
7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
8. Радиус описанной окружности правильного шестиугольника и его сторона равны.
Столбы базальтов от извержения старого вулкана. Снежинка. Пчелиные ульи. Кораллы, кристаллы и множество других структур, как биологических, так и небиологических, имеют форму шестиугольника. Почему природа, которая часто кажется такой беспорядочной и неправильной, предпочитает именно эту форму? Оказывается, все дело в геометрии и физике.
Соты строятся из пчелиного воска, вырабатываемого рабочими пчелами. Они вырабатывают воск из специальных желез в своем теле, которые затем смешивают с небольшим количеством меда и пыльцы, которую они разжевывают, чтобы получить пчелиный воск. Соты будут служить сосудами для хранения меда, а также камерами для выращивания молодых пчел.
Все это хорошо и замечательно, но почему шестиугольники?
Вымерший коралл Cyathophyllum hexagonum даже назван в честь своей шестиугольной формы, а некоторые диатомовые водоросли (основная группа водорослей) также имеют шестиугольную форму. Но, пожалуй, ни одна биологическая структура не имеет такой поразительной шестиугольной формы, как глаза стрекоз.
Глаза, состоящие примерно из 30 000 шестиугольников, переплетенных в ослепительное множество, являются одними из лучших в животном мире. Фактически, глаза стрекоз состоят из правильных шестиугольников, причем только три из этих шестиугольников встречаются в любой данной точке пересечения (или вершине).
У стрекоз два больших сложных глаза с тысячами шестиугольных линз (а также три глаза с простыми линзами, но оставим их пока в стороне). Шестиугольные линзы соединены между собой длинным тонким сетчатым каналом. На самом деле, у многих насекомых глаза имеют шестиугольную форму, и правило всегда гласит, что только три стенки клетки могут встречаться в любой вершине.
На самом деле, если мы на мгновение отойдем от биологического мира, то обнаружим, что точно такое же правило управляет чем-то совершенно другим: пеной из пузырьков.
Хотя пена пузырьков остается трудноразрешимой математической задачей, известно, что пена часто имеет тенденцию образовывать шестиугольные формы. В данном случае речь идет о поиске структуры с наименьшим общим поверхностным натяжением (что означает наименьшую площадь стены из мыльной пленки), и эта форма оказывается шестиугольником.
Конечно, структуры пены редко бывают идеально шестиугольными (а иногда они вообще не шестиугольные), потому что они также должны быть механически устойчивыми (и противостоять таким вещам, как ветер). Что еще более усложняет ситуацию, трехмерное расположение делает проблему еще более сложной. Несмотря на склонность к шестиугольникам, пена редко бывает упорядоченной.
На самом деле было удивительно много споров о том, какие формы может принимать пена, исследователи предлагали трехмерные 14-гранные многогранники и даже некоторые более безумные и беспорядочные формы. Но именно здесь становится интересно. Правила, управляющие формой ячеек в пене, похоже, также управляют некоторыми формами живых клеток. Дело не только в том, что глаза некоторых мух имеют такие же шестиугольные узоры, как и пена пузырьков, но и в том, что клетки внутри отдельных линз сгруппированы таким образом, что, похоже, повторяют геометрию пены пузырьков. Это поразительный случай, когда физика и математика направляют формы в биологическом мире.
Соединение колонн в Дороге гигантов в Северной Ирландии.
Но не вся лава остывает в одно и то же время, и некоторые участки могут все еще течь, в то время как другие уже затвердели, что может сделать формы более несовершенными. Поразительно, что часто угол удивительно близок к 120 градусам.
Если вы все еще не верите в существование шестиугольников в природе, вот еще один пример: снежинки.
Конечно, каждая снежинка уникальна, но все снежинки имеют шесть сторон или точек, и это связано с тем, как они формируются. Внешняя форма снежинок отражает их внутреннюю структуру. Гексагональная структура позволяет молекулам воды (с одним атомом кислорода и двумя атомами водорода) группироваться вместе наиболее эффективным образом.
Можете ли вы заметить шестиугольную структуру в этой снежинке?
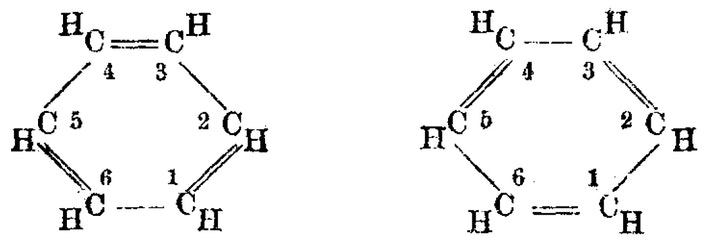
Если мы еще больше увеличим масштаб, то обнаружим еще одну форму шестиугольника. Как быстро отметит любой студент-химик, шестиугольники являются основой органической химии. Когда шесть атомов углерода соединяются, угол составляет 120 градусов, что уже должно быть знакомо. Шесть соединенных атомов углерода образуют идеальный шестиугольник, который также называется бензольным кольцом.
Есть еще один пример, который мы должны рассмотреть, и мы перейдем от очень маленьких к очень большим. Планета Сатурн имеет один из самых необычных шестиугольников в Солнечной системе: облачный узор длиной около 14 500 км; он больше, чем весь диаметр Земли. Шестиугольник состоит из газов, движущихся со скоростью 320 км/ч, и, как полагают, имеет толщину до 300 км.
Исследователи точно не знают, почему так происходит, но уже выдвинуто несколько теорий.
Почему же шестиугольники так часто встречаются в природе? Это зависит от того, как на это посмотреть. Это может быть эффективный способ сохранения массы или энергии, или просто способ расположить атомы таким образом, чтобы они были стабильны. Это может быть просто что-то, обусловленное геометрией.
Что такое правильный шестиугольник и какие задачи с ним могут быть связаны?
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3 ) 2 = 37,68 (см 2 ).
Осталось сосчитать объем: V = 37, 68 * 4 = 150,72 (см 3 ).
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Гексагон вокруг нас
В окружающей нас природе прослеживается строгая геометрия. Особое место отдано гексагону — правильному шестиугольнику. Эта фигура в тренде у насекомых, животных и даже неживой материи благодаря своим преимуществам в плане соответствия физическим законам.
Гексагон и пчёлы
Пчелиные соты, имеющие форму призмы с основанием в виде того самого гексагона, производят впечатление настоящего чуда с точки зрения инженерии. В том числе потому что:
Как столь сложную конструкцию выстраивают без расчетов и чертежей обычные насекомые? Тем более, что это — огромный коллектив, который работает одновременно, умудряясь как-то координировать свои действия. И в результате делает соты абсолютно одинаковыми.
По мнению Паппа Александрийского, философа из Древней Греции, пчелам свойственно «геометрическое предвидение». Данное им Господом. В 19-м столетии в «Монографии о пчёлах Англии» энтомолог У. Кёрби называл пчёл «математиками от Бога».
Ч. Дарвин был в этом совсем не уверен. Потому придумывал разнообразные эксперименты, призванные определить, строят ли пчёлы столь идеальные по геометрии соты, на основе врожденных или приобретенных способностей.
Почему шестиугольник?
Для геометрии это — простой вопрос. Когда нужно сложить ряд ячеек с одинаковыми размерами и формой так, чтобы заполнить ими определенную плоскость как можно полнее, подходят лишь 3 типа «правильных» (имеющих равные стороны и углы) фигур. То есть, речь идет о равносторонних:
В «личном» же первенстве данных вариантов, при равной площади, шестиугольникам потребуется наименьшая общая длина перегородок. Отсюда у пчелиного предпочтения гексагонов наблюдается непробиваемая логика. Чем меньше длина — тем меньше и воска, и труда.
Именно Дарвин первым выявил эту закономерность. А также был уверен, что благодаря естественному отбору, пчёлы получили инстинкты для создания ячеек наиболее рациональной формы. Однако современная наука, признавая за пчёлами особые способности в измерении толщины стенок или углов, обращает внимание на распространенность шестиугольников в природе вообще, а не только в ульях.
Пузыри на воде
Стоит подуть на пузырьки воздуха на водной поверхности, согнав их близко друг к другу, как они приобретают шестиугольную форму. И чем плотнее пузыри сгруппированы, тем явнее становится их шестиугольность.
А ведь при этом нет воздействия каких-либо организмов, работы над склейкой этих пузырей, подобной строительству пчел своих сот. Получившийся рисунок обязан своим появлением только физическим закономерностям.
Причина такой формы пузырей и образования именно таких «развилок» между мыльными стенками в том, что природу не менее пчёл заботит экономия сил и средств. Пузыри из мыльной пленки состоят из воды и слоя мыльных молекул. Поверхность жидкости под воздействием поверхностного натяжения сжимается так, чтобы занимать как можно меньшую площадь. Ровно как в случае с каплями дождя, принимающими при падении форму, стремящуюся к сферической. Потому что сфера отличается наименьшей площадью поверхности среди всех фигур с тем же объёмом. И на восковых листках водяные капли сжимаются до маленьких бусинок согласно все тому же закону.
То есть, именно поверхностным натяжением обусловлен узор, образуемый пузырями или пеной. Здесь прослеживается все то же стремление к конструкции, обеспечивающей минимальность общего поверхностного натяжения. А следовательно, мыльная мембрана обязана иметь и минимальную площадь. Причем стенки пузырей должны иметь конфигурацию, которая обязана обладать и механической прочностью. Такой, чтобы натяжение на перекрещивающихся направлениях имело идеальную сбалансированность. Точно так же, как обязателен баланс при возведении здания соборного типа.
Однако ошибочно принимать соты за этакое застывшее множество восковых пузырей. Потому что тогда будет трудно дать объяснение, каким образом подобные 6-угольные ячейки бумажные ячейки строят осы, создающие свои гнёзда из комков жёваной древесины. Во-первых, поверхностному натяжению здесь особая роль явно не принадлежит. А во-вторых, очевидно, что различные виды ос обладают разными врожденными инстинктами в плане «архитектурных школ», которые различаются весьма значительно.
Морской мир
У черепахи в центре панциря кожа также обладает 6-угольной формой. Именно потому что так наиболее эффективно можно покрыть плоскую поверхность. Для изогнутой же гексагоны не столь хороши. А панцирь черепах является именно таким. Отчего в нём присутствует кольцо и 5-угольников и вовсе неправильных фигур.
Вымершие уже кораллы под названием Cyathophyllum hexagonum даже имя своё получили благодаря 6-угольной форме. И такая группа водорослей, как диатомовые тоже обладают формой 6-угольника. Однако, сложно найти биологическую структуру, которая отличается более явной «гексагонностью», как глаз стрекозы.
Стрекоза и гексагон
Стрекозиный глаз включает порядка 30 тысяч 6-угольников, которые ещё и переплетены в умопомрачительной структуре. По сути, этот оптический аппарат, считающийся одним из лучших среди животных, состоит из гексагонов. При этом, лишь 3 из 6-угольников соприкасаются в любой вершине или определенной точке пересечения.
Напомним, что речь идет только о двух больших сложных глазах, а не о дополнительных трёх — с обычными линзами. Причём множество насекомых имеют глаза 6-угольной формы. И абсолютно всегда соблюдается тенденция, что только 3 стенки могут встретиться в одной вершине. А если отойти от мира биологии, обнаруживается, что такому же правилу подчинено всё, где встречаются гексагоны.
Вулканы
Извержения некоторых вулканов (в первую очередь — базальтовых пород) порождают изумительные образования 6-угольной формы. Озадачивая людей в течении столетий, такие гексагоны встречаются по всей планете: и примерно 6-угольные, и совершенно 6-угольные.
Наиболее известны два из них:
Снег кружится…
… летает и тает. Но, до того, как растаять, успевает подарить нам чудное зрелище — снежинку. При уникальности каждой из них абсолютно все обладают шестью сторонами или точками. В этой форме снежинок отражается её внутренняя структура. Именно благодаря гексагональной структуре молекулы воды группируются максимально эффективно.
Самый крупный гексагон
На макроуровне одним из наиболее известных 6-угольников считается гигантское облако гексагональной формы на северном полюсе планеты Сатурн. Длина его составляет примерно 14,5 тыс. км, что больше диаметра Земли. А каждая сторона Гексагона Сатурна (так его астрономы и называют) достигает в длину 13,8 тыс. км.
Этот гексагон образуют газы, слой которых, предположительно достигает толщины в 300 км и движется со скоростью 320 км/ч. Облако вращается — 1 оборот за 10 ч. 39 мин. Не в пример остальным облакам на Сатурне, это не перемещается, постоянно находясь на одном месте.
Над южным полюсом планеты ничего подобного нет. Но есть огромная воронка в атмосфере, ровно такая, как в центре Гексагона Сатурна.
На клеточном уровне
Вышеописанные правила работают и в узорах, присущих живым организмам. Так, из групп 6-угольных ячеек состоит не только фасеточный глаз мухи, но и в каждой такой ячейке обнаруживаются гроздья из 4-х светочувствительных клеток, напоминающие мыльный пузырь.
Для строительства подобных гексагонов не требуется сложных генетических инструкций. Физические законы всё сделают сами. Пористую совокупность ячеек представляет собой экзоскелет такого животного, как морской ёж Cidaris rugosa. На этой защитной раковине размещены опасные на вид колючки из минерала, из которого состоят мел и мрамор. Благодаря открытой решетчатой структуре этот материал отличается прочностью и малой массой, подобно пенометаллу, применяемому в авиапромышленности.
Экзоскелеты некоторых видов морских губок образуют минеральные стержни, которые соединены подобно «паутинке» с детских площадок. Также они очень напоминают по форме пузыри в мыльной пене. Без малейшего допущения «случайного совпадения», потому что такая архитектура диктуется поверхностным натяжением.
Этот процесс, называемый биоминерализацией, даёт особенно впечатляющие результаты и у других морских животных, например — диатомей и лучевиков. Ряд из них обладают аккуратными экзоскелетами из ячеек в форме гексагонов, этакими минеральными «морскими сотами». Естествоиспытатель, философ и художник 19-го столетия Э. Геккель, увидев их в микроскопе, использовал эти формы, как главное украшение своей серии рисунков «Красота форм в природе», оказавшей сильное влияние на многих художников до нашего времени.
Геккель считал такие конструкции доказательством истинной креативности природы, её предпочтением таких узоров и порядков, которое встроено в основу естественных законов. Упорядоченность остается неудержимым импульсом живой и неживой природы. Именно поэтому мы и выбрали для нашей компании гордое имя «Гексагон». Как символ:
И этими же принципами руководствуемся при создании нашей продукции.
Правильный шестиугольник и его свойства
Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
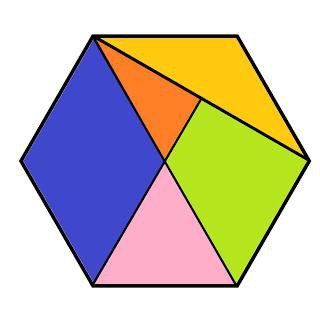
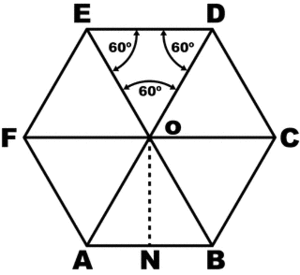
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
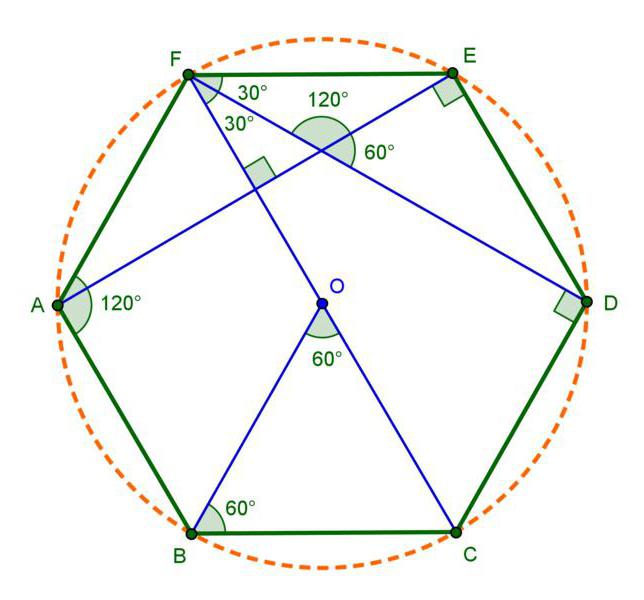
Описанная окружность и возможность построения
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
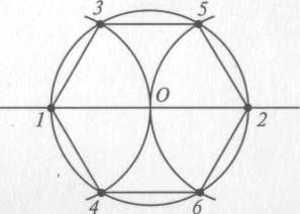
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
Вписанная окружность
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
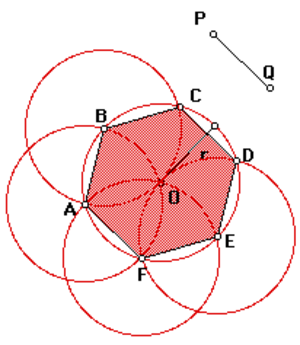
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
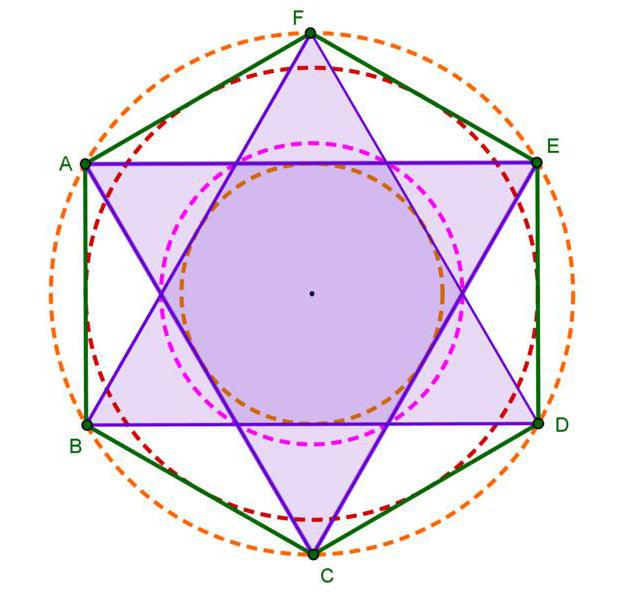
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.