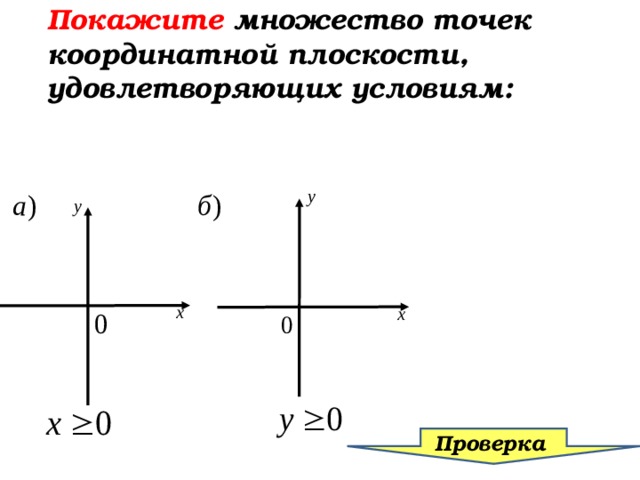
каким условием можно задать множество точек координатной плоскости изображенное на рисунке
Урок алгебры в 7-м классе по теме «Множества точек на координатной плоскости»
Разделы: Математика
I. Оргмомент
II. Актуализация знаний

2. Построить отрезок LE, если L(–1; 2), Е(4; 5).
Построить прямую РТ, если Р(0; 3), Т(–1; –2)
III. Постановка проблемы

Отметьте указанные точки на координатных плоскостях
1) А(3; 1), В(4; –1), С(–5; –2).

2) М(3; –2), N(–4; –2), К(1.5; –2)



В первом случае?

Что общего?
Мы выяснили, что общее в 2–4 рисунках то, что точки лежат на одной прямой.
IV. «Открытие» детьми нового знания


Какое условие является общим для этих точек?
А как это условие записать на языке алгебры? у = 3
(ордината равна 3)
На рис.2 проведите через отмеченные точки у = – 2
прямую, запишите множество этих точек.
Проведите на остальных рисунках через отмеченные точки прямые.
А как бы вы записали на языке алгебры множества точек, изображенных на рисунке 3? 4? 5?
Подумайте, а затем проверим правильность записей.

Множество точек расположенных где? На координатной плоскости

А цель урока?
Учитель еще раз формулирует тему и цель урока, записывает тему на доске.
Изобразите на координатной плоскости множество точек, удовлетворяющих условию:
У обучающихся На доске

х = – 4

у = – 4
у = 1
Проверяем правильность построения и записи.
А теперь давайте попробуем изобразить множество точек, удовлетворяющих условию х > 3.
Как можно это условие прочитать на русском языке? – точки, большие 3
Чтобы построить точку в координатной плоскости, необходимо, что знать?


Где будут располагаться точки, абсцисса которых больше 3?
Покажите несколько таких точек

А множество всех точек удовлетворяющих условию х > 3 можно показать с помощью штриховки
х > 3 задает полуплоскость, расположенную правее прямой х = 3 и все точки этой прямой.

Проверяем правильность построения.
Постройте множество точек у > 1.
Каким свойством обладают точки этого множества у них ордината больше 1
А как они должны располагаться относительно – выше
прямой у = 1
А точки прямой у = 1 удовлетворяют условию y > 1 нет
А как это показать? – не знаем

Изобразим множество точек, удовлетворяющих условию у > 1.
Приглашается ученик к доске.
Изобразите множество точек, удовлетворяющих условию:
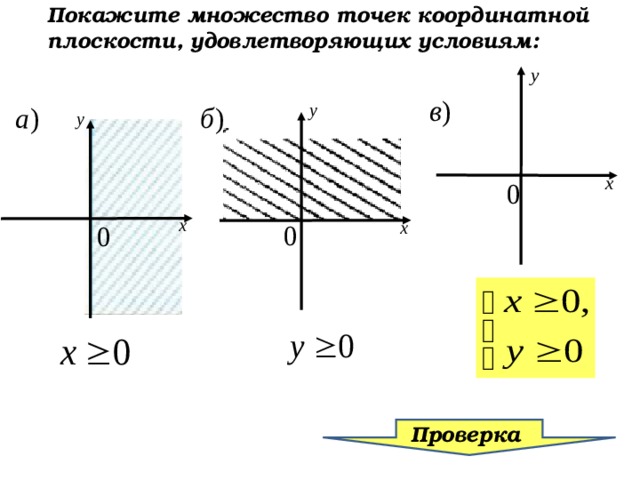
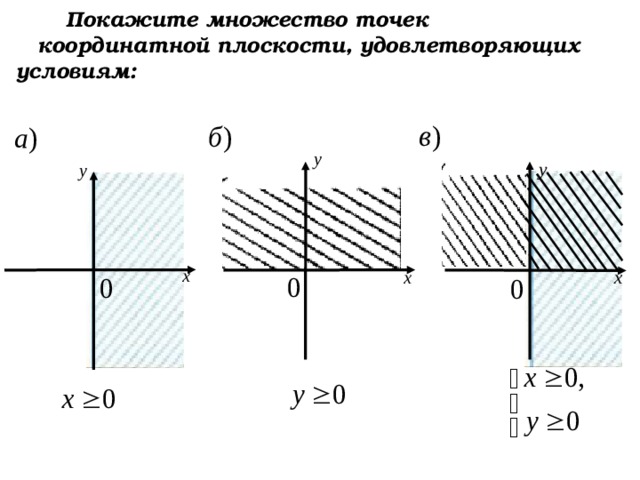
Выделите множество точек, удовлетворяющих одновременно всем этим условиям.
Какую фигуру получили?
VI. Самостоятельная работа с последующей самопроверкой
1. Опишите на алгебраическом языке множества точек, изображенные на рисунках.
1. 
2. Изобразите на координатной плоскости множества точек, удовлетворяющих условию:
Множество точек на координатной плоскости
Просмотр содержимого документа
«Множество точек на координатной плоскости»
Урок алгебры в 9 классе
Ни одна наука так не укрепляет веру в силу человеческого разума, как математика.
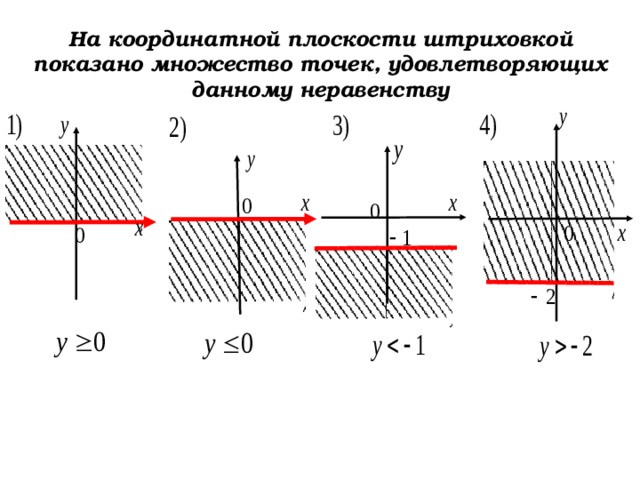
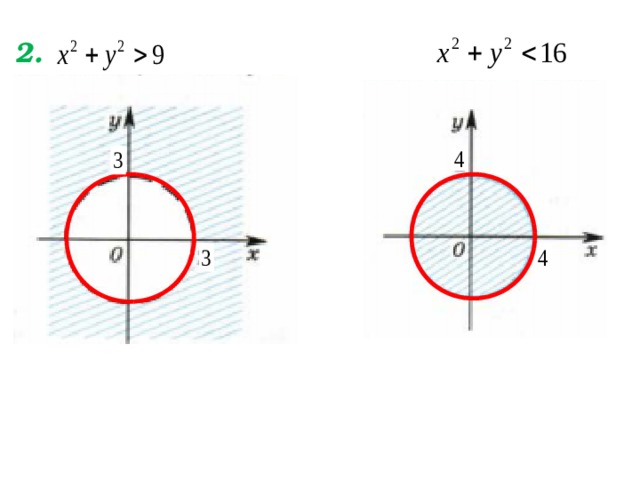
На координатной плоскости штриховкой показано множество точек, удовлетворяющих данному неравенству
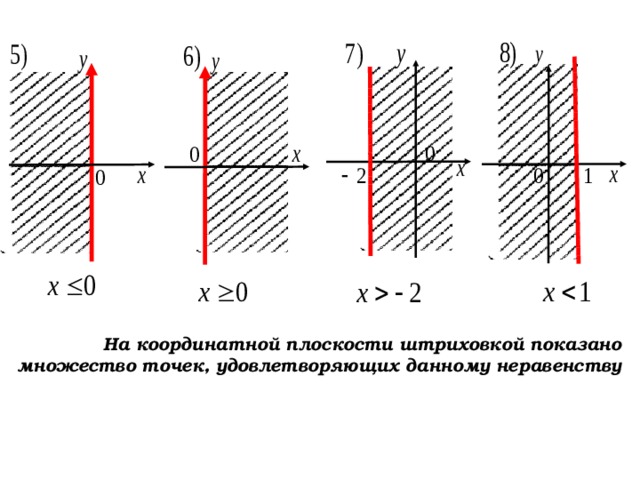
На координатной плоскости штриховкой показано множество точек, удовлетворяющих данному неравенству
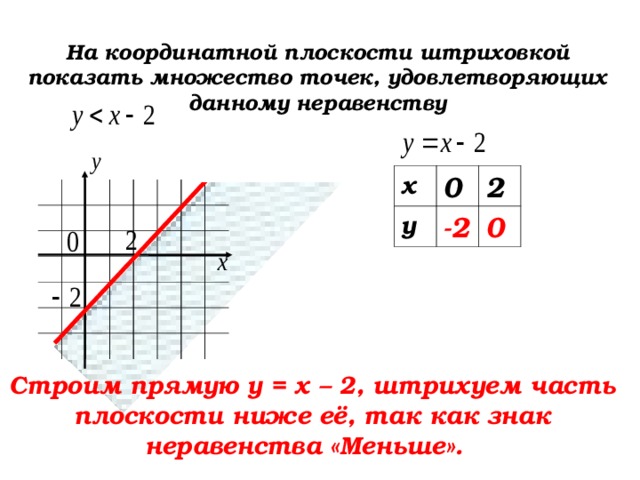
На координатной плоскости штриховкой показать множество точек, удовлетворяющих данному неравенству
Строим прямую у = х – 2, штрихуем часть плоскости ниже её, так как знак неравенства «Меньше».
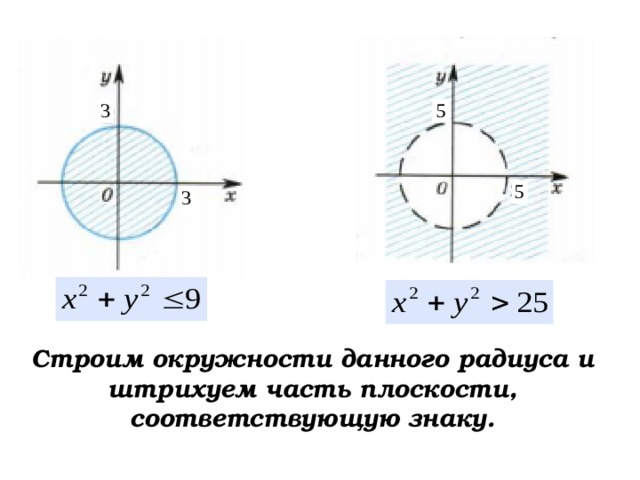
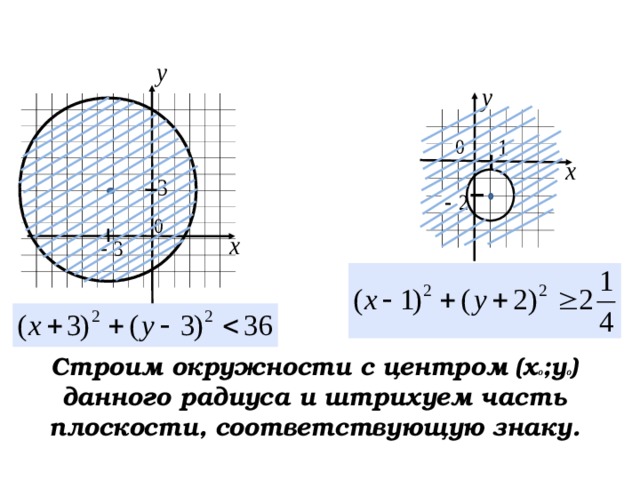
Строим окружности данного радиуса и штрихуем часть плоскости, соответствующую знаку.
Строим окружности с центром (х 0 ;у 0 ) данного радиуса и штрихуем часть плоскости, соответствующую знаку.
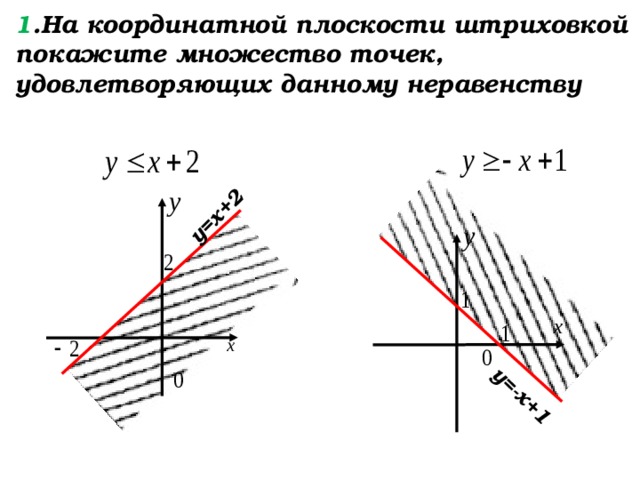
1 .На координатной плоскости штриховкой покажите множество точек, удовлетворяющих данному неравенству
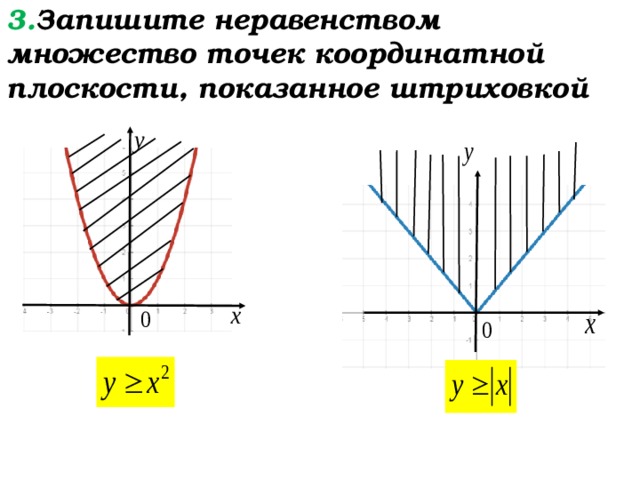
3. Запишите неравенством множество точек координатной плоскости, показанное штриховкой
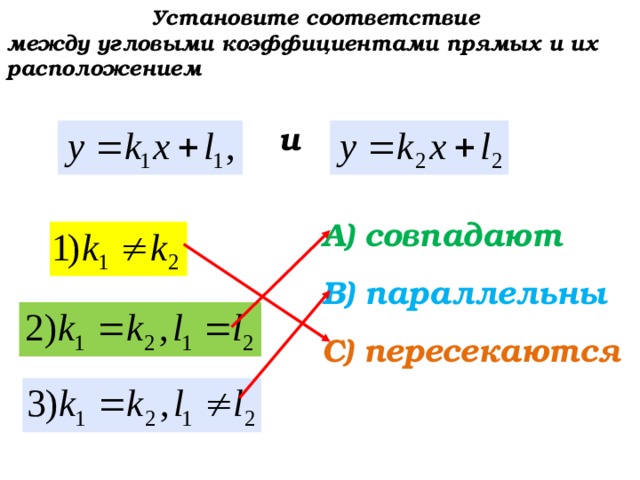
между угловыми коэффициентами прямых и их расположением
между угловыми коэффициентами прямых и их расположением
между угловыми коэффициентами прямых и их расположением
между угловыми коэффициентами прямых и их расположением
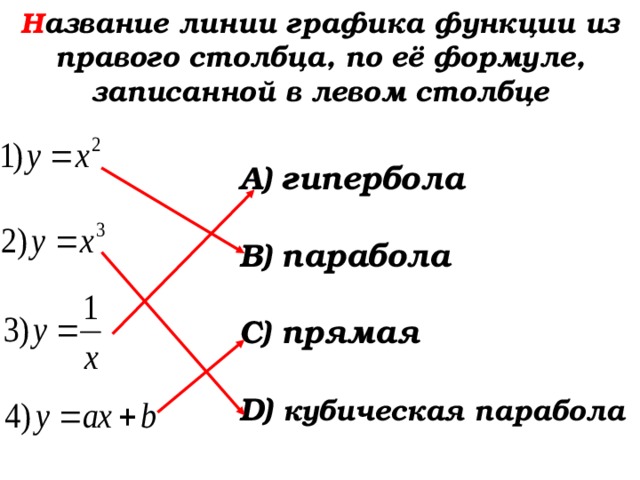
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
Н азвание линии графика функции из правого столбца, по её формуле, записанной в левом столбце
Назовите фигуру на координатной плоскости, заданную условием:
Назовите фигуру на координатной плоскости, заданную условием:
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Две параллельные прямые
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Две параллельные прямые
Две параллельные прямые
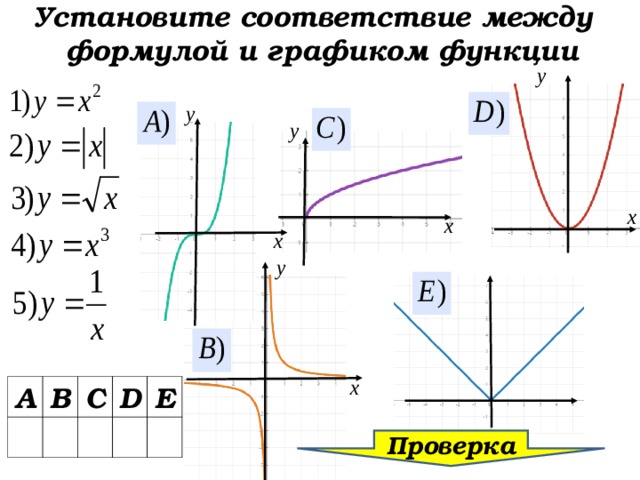
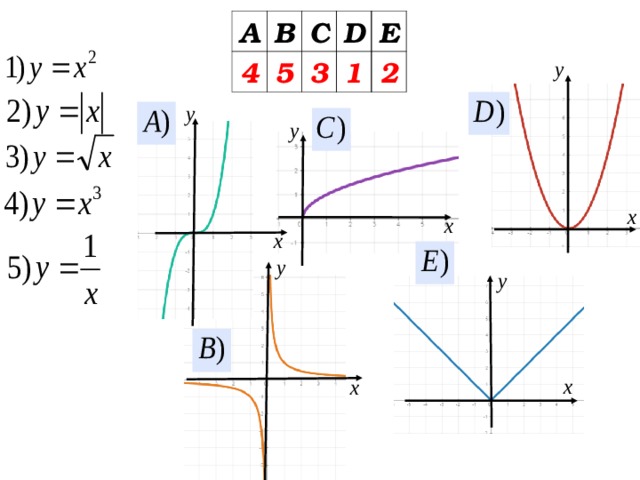
Установите соответствие между формулой и графиком функции
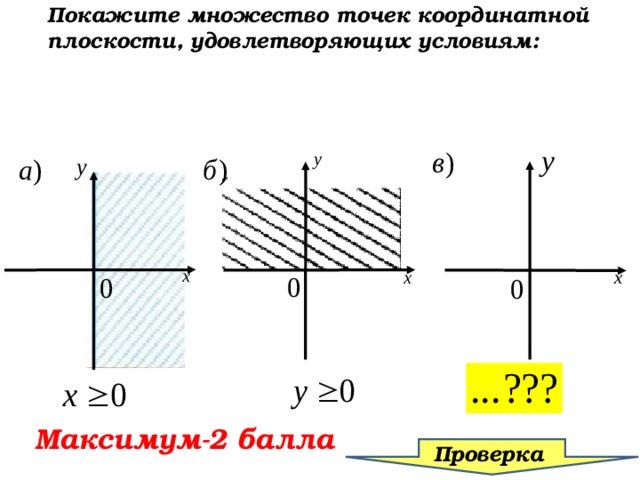
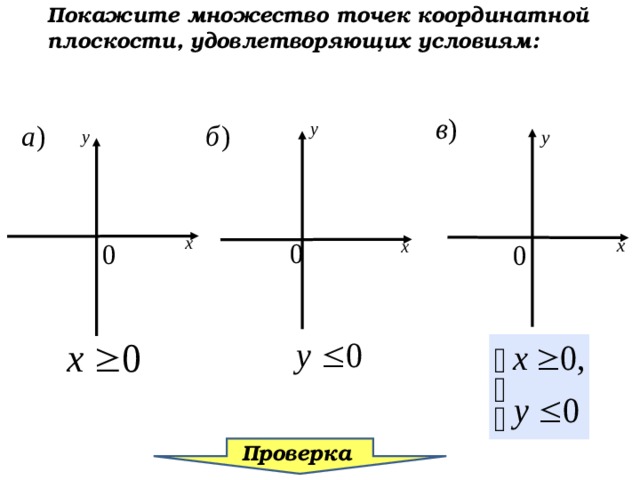
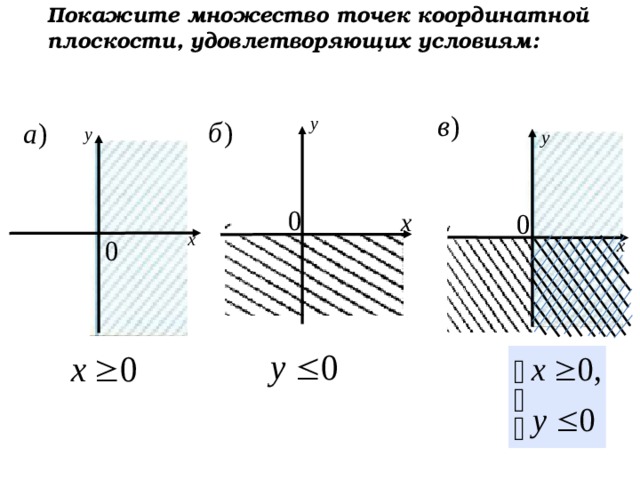
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
Покажите множество точек
координатной плоскости, удовлетворяющих условиям:
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
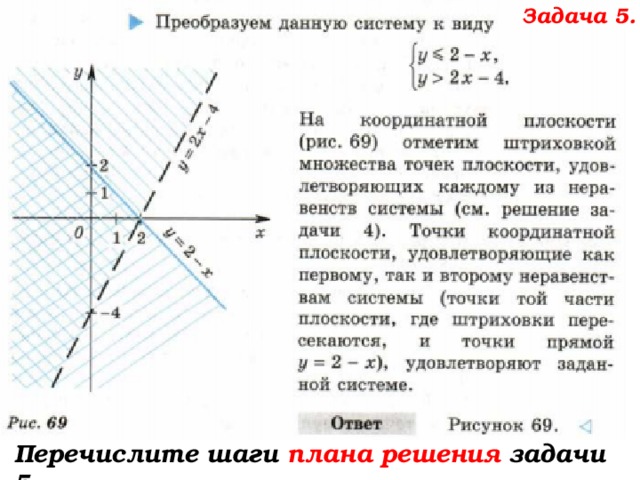
Задача. На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств
На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств
Делаем выводы по решению.
Учимся решать подобные задачи.
Какое преобразование нужно выполнить в первом неравенстве?
Каков следующий шаг решения?
Презентация была опубликована 8 лет назад пользователемДенис Охохонин
Похожие презентации
Презентация на тему: » « Красивые множества на плоскости ». П р и м е р. Изобразим на координатной плоскости множество точек, заданное условием у = | x | + x. При х 0 | x |» — Транскрипт:
1 « Красивые множества на плоскости »
2 П р и м е р. Изобразим на координатной плоскости множество точек, заданное условием у = | x | + x. При х 0 | x | = x, и данное условие запишется в виде у = 2х. При х
8 |y| + y = |x| + x При у 0, у + у = х + х, 2у = 2х, т. е. у = х
10 « Геометрическая интерпретация неравенств с двумя переменными » переменными »
x.» title=»П р и м е р 1. Выясним, какое множество точек координатной плоскости задаётся неравенством у > x.» > 11 П р и м е р 1. Выясним, какое множество точек координатной плоскости задаётся неравенством у > x. x.»> x.»> x.» title=»П р и м е р 1. Выясним, какое множество точек координатной плоскости задаётся неравенством у > x.»>
13 П р и м е р 2. Построим множество точек координатной плоскости, которое задаётся системой неравенств у
20 в) у |x|, y 5; х у У =|x|, у =5
22 З а д а н и е 4. Покажите штриховкой часть координатной плоскости, которая расположена ниже каждой из прямых х + 3у = 15 и 2х + у = 12, ограничена горизонталями у = 0 и у = 5, а также вертикалями х = 0 и х = 5. Задайте это множество точек системой неравенств. х +3у = 15 х у 2х + у = 12 У = 0 У = 5 х = 0 х = 5 х + 3у 15 2х + у 12 у 0 у 5 х 0 х 5
26 « Графики уравнений, содержащих модули » содержащих модули »
28 П р и м е р 2. Построим график уравнения у = x 2 – 2| x |. если х 0, то у = x 2 – 2 x ; если х
30 З а д а н и е 1. Постройте график уравнения: а) y = |2x – 4|; в) y = |x 2 – x – 2|; б) y = |x 2 – 3|; г) y =. х у х у
32 y = |x 2 – x – 2|; х у 1/ /4
37 З а д а н и е 4. Постройте график уравнения: а) | y | = | x |;. х у
38 б) |y| + |x| = 1 При у 0, |y| =у и | х | =х, т. е. у+х=1, у=-х+1 При у 0, |y| =-у и | х | =х, т. е. –у+х=1, у=х-1
43 Как вырезать бумажные снежинки?
44 З а д а н и е 1: Возьмите полоску бумаги шириной 5 см и длиной около 20 см. Сложите её «гармошкой» и нарисуйте какой-нибудь рисунок, касающийся линии сгиба (рис. 10, а). Вырежьте фигуру, оставляя участки на линиях сгиба неразрезанными, разверните полученную «гармошку». Если ленту предварительно сложить вдвое вдоль, а затем «гармошкой», то получится лента, симметричная относительно горизонтальной оси (рис 11)
46 Пусть мы вырезали не симметричный трафарет (рис. 13, а) передвинем трафарет вправо на расстояние, равное ширине трафарета (такое преобразование называют параллельным переносом). Получим бордюр, показанный на рисунке 13, б. Отражаясь симметрично относительно вертикальной оси, трафарет даст бордюр, показанный на рисунке 13, в. Если трафарет поворачивать вокруг точки О (центра симметрии) на 180 0, то бордюр уже будет иным (рис 13, г). Отражением относительно горизонтальной оси и последующим переносом трафарета получим ещё один орнамент (рис. 13, д). Рис 13
47 З а д а н и е 2: Возьмите трафарет, симметричный относительно вертикальной оси, например, такой, как на рисунке 14. Сколько различных бордюров можно получить с его помощью? Какие преобразования дают одинаковые бордюры? Объясните, почему так получается. Вырежьте трафарет и изобразите эти бордюры. Определите, сколько разных бордюров получится из трафарета, симметричного относительно горизонтальной оси (рис. 15). Какие преобразования дают одинаковый результат? Почему? Мы можем взять и трафарет, рисунок которого совпадает сам с собой при повороте его на вокруг центра (точки, лежащий внутри рисунка), например такой как на рисунке 16. Рис 14 Рис 15 Рис 16 З а д а н и е 3: Нарисуйте различные бордюры с его помощью. Совпадают ли результаты каких-либо преобразований?
49 На Руси издревле старались украсить терема, церкви. Они придумывали удивительно замысловатые орнаменты, в основном цветочные. В XVII в. русский зодчий Степан Иванов создал свой орнамент, который назвал «Павлинье око», так как он был похож на рисунок пера павлиньего хвоста.
51 З а д а н и е 4: Рассмотрите орнамент, изображенный на рисунке 19, выделите в нем трафарет. Подумайте, к какому типу можно его отнести. Как получился этот бордюр? Рис 19
52 Определите, из какого трафарета и с помощью какого преобразования получены бордюры, показанные на рисунке 20, а-е., 21, а-ж. Рис 20
53 а) б) в) г) д) е) ж) Рис.21
55 3. Домашнее задание. 1) Вырезать свои оригинальные ленты. 2) Придумать трафарет и нарисовать с его помощью разные бордюры. 3) Придумать и нарисовать свои трафареты пяти видов.
57 Вы, конечно, знаете, что такое паркет. Обычно, паркет выкладывают из дощечек, имеющих форму прямоугольника, и чаще всего «ёлочкой». Но составление паркета может быть и искусством. Им в совершенстве владели крепостные мастера, создававшие паркеты во дворцах царей и вельмож
58 Изображен паркет из правильных треугольников, переходящий в паркет из правильных шестиугольников. Выложить паркет можно и из нескольких видов правильных многоугольников. Например, паркет на рисунке 24 составлен из правильных треугольников, четырехугольников и шестиугольников. В каждой вершине сходятся треугольник, два квадрата и шестиугольник.
59 З а д а н и е 1: Из каких фигур составлен паркет, изображенный на рисунке 25? Какие фигуры сходятся в каждой его вершине? Вырежьте из цветной бумаги необходимые фигуры и выложите их на столе в виде такого паркета. З а д а н и е 2: Из правильных восьмиугольников и квадратов можно сложить паркет так, как показано на рисунке 26. Найдите величину угла правильного восьмиугольника. Рис. 25Рис. 26
60 Но не только правильные многоугольники могут служить для составления паркета. З а д а н и е 3: Вырежьте из бумаги 20 одинаковых произвольных треугольников. Выложите из них паркет. Всегда ли это можно сделать? Почему? З а д а н и е 4: Вырежьте из бумаги 10 одинаковых четырехугольников произвольного вида и выложите из них паркет. Объясните, почему это можно сделать. В этом вам поможет рисунок 27. Рис. 27
62 Рис. 28 З а д а н и е 5: Начертите в тетради паркеты из элементов изображенных на рисунке 28. З а д а н и е 6: Рассмотрите внимательно паркеты, изображенные на рисунке 29, они созданы вашими сверстниками. Попробуйте выделить элемент одного из паркетов и нарисовать его.
63 3. Домашнее задание. Придумать свой паркет.
67 Построить орнамент можно с использованием трафарета. Для этого положим на лист бумаги линейку, приложим к ней трафарет и обведем контур отверстия карандашом (рис. 31). Линейка задает нам линию сдвига. Сдвинем трафарет вдоль линейки и вновь обведем контур отверстия. Рис. 31 З а д а н и е 1. Орнамент, изображенный на рисунке 32, построен с помощью трафарета буквы «ж» параллельным переносом вдоль вертикальной прямой на 1 см. Возьмите какой-нибудь трафарет и постройте с его помощью свой орнамент Рис. 32
68 З а д а н и е 2.Рисовать орнаменты очень удобно на клетчатой бумаге. Перенесите рисунок 33 в тетрадь и продолжите построение орнамента. Раскрасьте повторяющийся элемент орнамента. На отрезке, какой длины сдвигается этот элемент? З а д а н и е 3.Нарисуйте от руки орнамент, который получается при параллельном переносе элемента (рис. 34) вдоль вертикальной прямой. Рис.33 Рис. 34
69 З а д а н и е 4. Орнамент на рисунке 35– часть украшения деревенской избы. Изобразите повторяющийся элемент этого орнамента. З а д а н и е 5. Элементы древних орнаментов можно встретить и в произведениях современных мастеров, например на решетке одного из московских мостов (рис. 36) Рис. 35 Рис. 36
70 З а д а н и е 6. Постройте орнамент по следующему алгоритму: 1. перенесите четырехугольник в тетрадь (рис. 37); 2. нарисуйте второй четырехугольник, полученный сдвигом первого на 2 клетки вправо и 2 клетки вверх; 3. нарисуйте третий четырехугольник, полученный сдвигом второго на 2 клетки вправо и 2 клетки вниз; 4. последовательно повторите пункты 2 и 3. Раскрасьте получившийся орнамент. Рис. 37 З а д а н и е 7. Орнамент в задании 6 получается с помощью двух параллельных переносов. Придумайте и постройте свой орнамент, который также получается с помощью двух параллельных переносов.
71 3. Домашнее задание. Придумайте и постройте свой орнамент, который получается с помощью двух параллельных переносов.