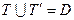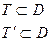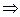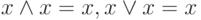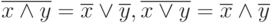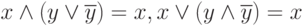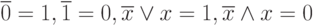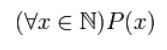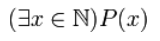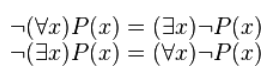каким образом предикат можно превратить в высказывание
Обращение предиката в высказывание
Определение: Предложение с одной или несколькими переменными, которое обращается в высказывание при подстановке вместо переменных их значений, называется высказывательной формой или предикатом.
В зависимости от числа переменных предикаты бывают одноместными, двухместными и т.д. n –местные.
Обозначаются: А(х) – одноместный
В(х,y) – двухместный и т.д.
С каждым предикатом связывают три множества:
1) область определения предиката: DA(x) – это множество значений переменной, при которых предикат обращается в высказывание.
2) множество истинности предиката ТА(х) – это множество тех значений переменных из области определения предиката, при котором предикат обращается в истинное высказывание.
3) множество ложности предиката: 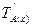
Между этими множествами существует вполне определённая связь:
 |
Множества истинности и множества ложности предиката дополняют друг друга до области определения предиката.
Пример 1. На множестве R задано предложение Х 2 – 1 = 0. Является ли оно предикатом? Какова область определения? Множество истинности?
1) 
2) при Х = 1, 1 2 – 1 = 0 – это предложение обращается в
это одноместный предикат: А(х): Х 2 – 1 = 0
ТА =
Видим, что все отношения выполняются: 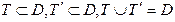
1) – это предложение с переменной, но оно является истинным высказыванием, а не предикатом.
Пример 3: С(х,у): x + y = 7,
1) предложение с двумя переменными х и y
2) обращается в высказывание, например, при x = 3 y = 5
С(3,5): 3 + 5 = 7 – высказывание (не важно сейчас какое).
Dc – это множество пар действительных чисел:
Dс =
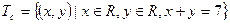
Если подставлять значение только одной переменной, то предикат станет одноместным предикатом.
Пусть x = 10 тогда 
Предикат можно обратить в высказывание двумя способами:
1 способ: путём подстановки в предикат конкретного значения переменной (переменных)
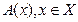



2 способ: путём навешивания кванторов.
Кванторы бывают двух видов:
1) квантор всеобщности, который выражается словами: любой, каждый, всякий, все, и обозначается: 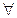
2) квантор существования: выражается словами: найдётся, существует, и обозначается 
Пусть на множестве Х задан одноместный предикат А(х). Предложение: для любого Х из множества Х выполняется А(х) –это высказывание, которое ложно, если найдется хотя бы одно значение переменной x 
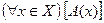
Предложение: существуют элементы x
Запишем это высказывание так: 
Пусть 
1) 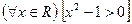
2) 

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Высказывания и предикаты. Кванторы
п.1. Высказывания
Например:
«Число 13 – нечётное» – высказывание, истинное
«2 + 2 = 5» – высказывание, ложное
«Мы живём в XXI веке» – высказывание, истинное
«Который час?» – не высказывание, т.к. вопросительное предложение
«Вася Пупкин – хороший человек» – не высказывание, т.к. неоднозначно. Но, если определить множество людей, которые оцениваются, и правила их оценки так, что предложение приобретёт однозначность, оно станет высказыванием.
Например:
A: натуральное число a делится на 2;
B: натуральное число a чётное.
Заметим, немного забегая наперёд, что в данном случае из А следует В, и из В следует А. Говорят, что эти высказывания эквивалентны: A ⇔ B.
п.2. Предикаты
Например:
P(x): x – объект с четырьмя ногами
При x = слон – предикат становится истинным высказыванием, P(«слон» )=1
При x = муравей – предикат становится ложным высказыванием, т.к. у муравья 6 ног, P(муравей)=0
При x = стол – предикат становится истинным высказыванием, P(«стол» )=1
При x = человек – предикат становится ложным высказыванием, т.к. у человека 2 ноги, P(человек)=0
Например:
P(x):|x| ≥ 0 – выполняется при любом значении x, это тождественный предикат.
\(\mathrm
Например:
P(x, y): x делится на y – двуместный предикат, который становится истинным высказыванием на парах значений переменных (15;5), (14;7), (16;4) и т.д.
P(a, b):(a + b) 2 = a 2 + 2ab + b 2 – является тождественным двуместным предикатом, т.к. выполняется для любых a и b.
п.3. Кванторы
«для любого…», «для всех…», «любой…»
Единственности и существования
«существует точно одно такое, что…», «существует и единственно…»
Существуют натуральные числа, которые делятся на 13
Существуют треугольники, у которых все углы равны
Например, равносторонний треугольник со стороной 1
Любое натуральное число делится на 5
Например x = 6 на 5 не делится
У любого выпуклого четырехугольника диагонали перпендикулярны
Например, у прямоугольника со сторонами 3 и 4 угол между диагоналями ≈ 74° ≠ 90°
Разность квадратов двух любых выражений равна произведению суммы и разности
Сумма углов любого треугольника равна 180°.
Третий класс задач (теорема) – самый сложный, т.к. требует не просто одного примера, а доказательства в общем случае.
п.4. Примеры
Пример 1. Запишите по два высказывания (A – истинное, B – ложное), относящиеся к
а) физике
A: Плотность равна отношению массы тела к его объему.
B: КПД механизма может быть больше 1.
б) химии
A: Гидроксид натрия – сильное основание.
B: Сульфат натрия – нерастворимая соль.
в) географии
A: На Земле шесть материков.
B: На Земле три океана.
Пример 3. С каким из кванторов предикат x 2 + 4 = 12 станет истинным высказыванием?
Если запишем (∀x) x 2 + 4 = 12 – это ложное высказывание, т.к., например, при x=0 оно не выполняется.
Если запишем (∃x) x 2 + 4 = 12 – это истинное высказывание, т.к., например, при \(\mathrm
Если запишем (∃x!) x 2 + 4 = 12 – это ложное высказывание, т.е. решений у данного уравнения не одно, а два: \(\mathrm
Ответ: квантор существования ∃.
Высказывания и предикаты
Операция f называется n-местной, если она связывает n операндов (объектов – участников этой операции ).
Пример. Рассмотрим словосочетания:
Высказывание должно быть однозначно истинным или однозначно ложным, поэтому высказываниями являются только утверждения 1), 4), 6).
Истинным будет, например, сложное высказывание : «Зима – холодное время года и зимой носят пальто», а ложным будет, например, высказывание : «Некоторые ходят в пальто, поэтому на улице зима». Придумайте другие примеры.
Предикат – высказывательная форма с логическими переменными (множество значений этих переменных вполне определено), имеющая смысл при любых допустимых значениях этих переменных. Количество переменных в записи предиката называется его местностью.
Простые высказывания или предикаты не зависят от других высказываний или предикатов («не разбиваемы на более простые»), а сложные – зависят хотя бы от двух простых.
Логической (булевой) функцией f(х) называется некоторая функциональная зависимость, в которой аргумент х – логическая переменная с заданным множеством изменений аргумента, а значения функции f(x) берутся из двухэлементного множества R(f) = <1,0>.
Аксиома двойного отрицания:
Аксиомы переместительности операндов (относительно операций дизъюнкции и конъюнкции ):
Аксиомы переместительности операций дизъюнкции и конъюнкции (относительно операндов):
Аксиомы одинаковых операндов:
Аксиомы поглощения (множителем — множителя-суммы или слагаемым — слагаемого-произведения):
Аксиомы распределения операции ( дизъюнкции относительно конъюнкции и наоборот):
Аксиомы де Моргана (перенесения бинарной операции на операнды):
Аксиомы нейтральности (взаимноинверсных множителей или слагаемых):
Из этих аксиом следует ряд полезных соотношений, например,
Способы получения высказываний из предикатов
1. Подстановка значений переменных.



Значения переменных, при которых предикат превращается в истинное высказывание, называются значениями истинности предиката.
Множество всех значений истинности предиката называется областью истинности предиката.
2. «Навешивание» кванторов на переменные

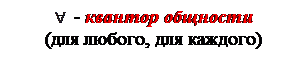

Пример.
«Навесим» кванторы на переменную предиката 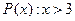


«Навешивание» кванторов на переменные двухместного предиката:
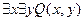
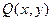

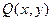

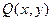
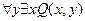
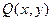
Пример.
«Навесим» кванторы на переменные предиката 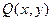

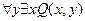
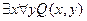


Понятие множества


Пример.
Множество домов на данной улице, множество натуральных чисел, множество студентов группы и т. д.
Множества обычно обозначают заглавными латинскими буквами – А, В, С, D, X, Y…, элементы множества строчными латинскими буквами – a, b, c, d, x, y…

Пример.U – множество людей на земле, А – студенты группы Эп-505.



Не нашли, что искали? Воспользуйтесь поиском:
Предикаты и кванторы
Вы будете перенаправлены на Автор24
Понятие предиката
Предикатом в программировании является функция, которая принимает один или более аргументов и возвращает значения булева типа.
Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:
Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:
Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.
Примеры предикатов
Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.
Готовые работы на аналогичную тему
Операции над предикатами
Рассмотрим применение операций алгебры логики к предикатам.
Логические операции:
Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.
Кванторы
Чаще всего используют кванторы:
В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.
Примеры применения кванторов
С помощью квантора всеобщности можно записать следующие ложные высказывания:
который будет иметь вид:
Для записи истинных высказываний используем квантор существования:
Запись будет иметь вид:
Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.
Операции над кванторами
Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:
Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них: