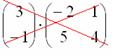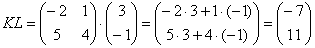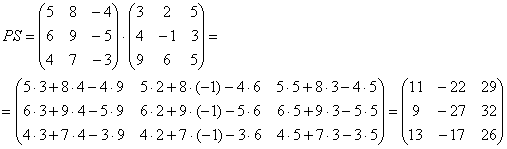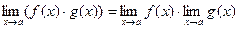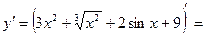какие матрицы можно умножать

Знакомство с матрицами

Понятие и базовые операции.

Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:

Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.

Что такое матрица

Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.

Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.

Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.

В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.

В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.

Общая схема матрицы Пример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число три

Простые операции с матрицами

Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.

И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.

Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыре Перед матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычислений

Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.

Пример умножения матрицы на число

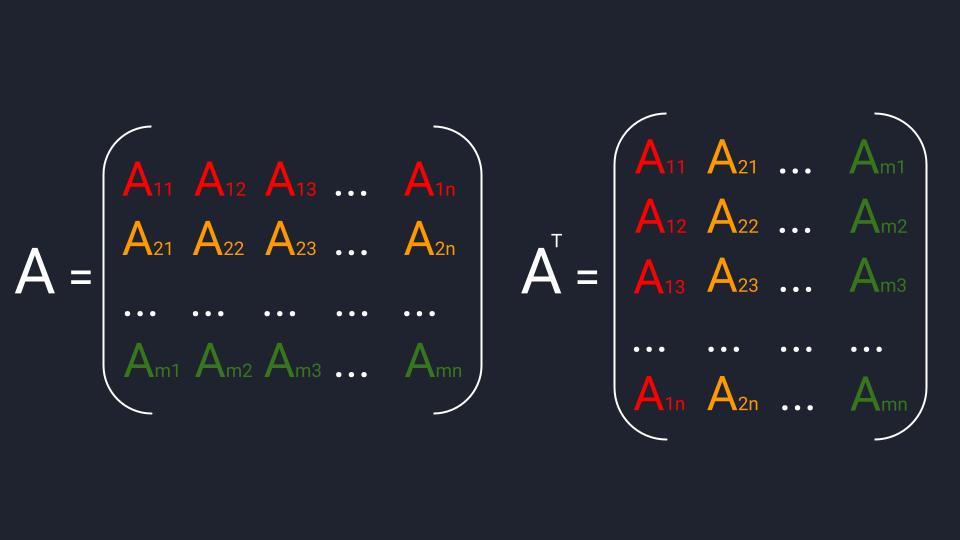
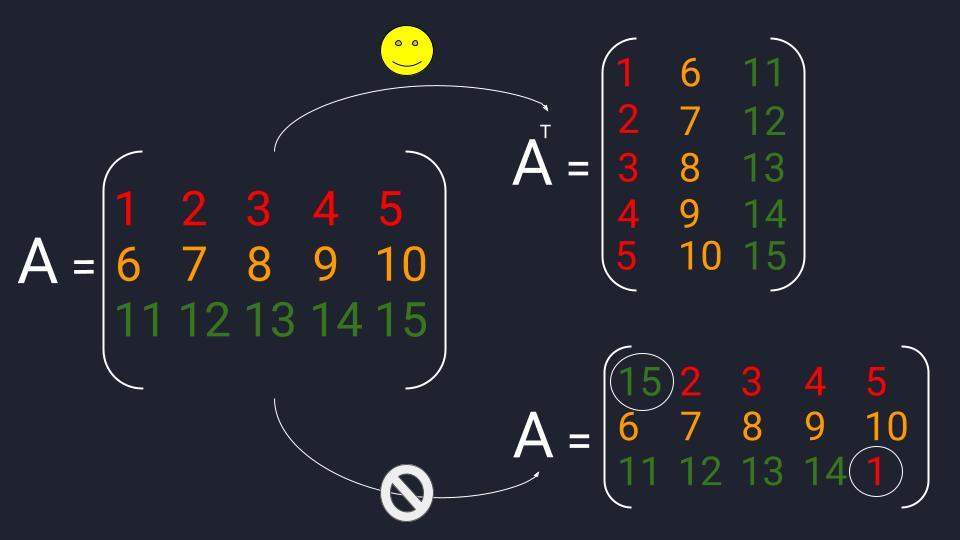
Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.

⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.

Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицы Пример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т» Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правил

Сложение и вычитание матриц

Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.

Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами Пример вычитания двух матриц

Умножение матриц

Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:

Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.

Формула умножения матриц Пример умножения квадратных матриц размерностью 2×2

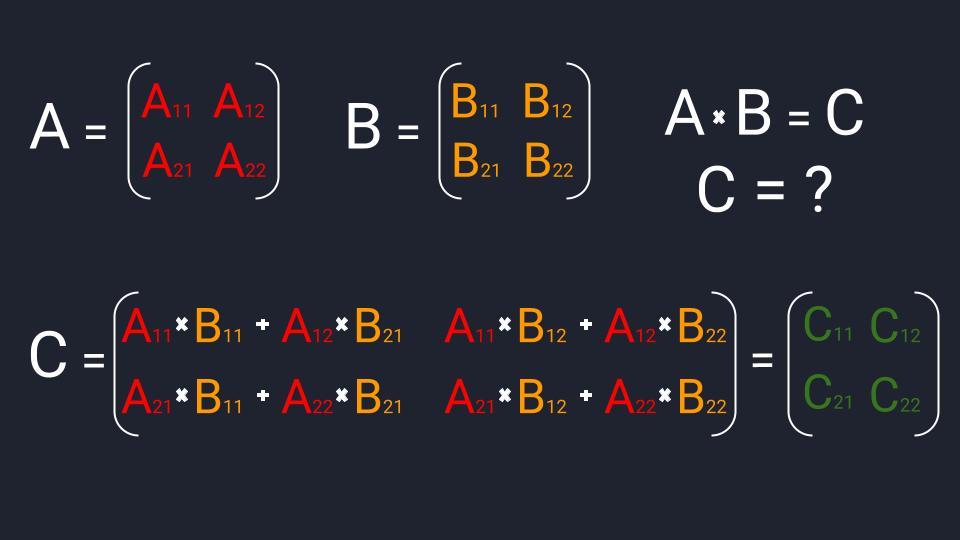
Что дальше

В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽

Источник

Какие матрицы можно умножать?

Чтобы матрицу можно было умножить на матрицу необходимо, чтобы число столбцов матрицы равнялось числу строк матрицы .

Пример 4:
Можно ли умножить матрицу на матрицу ?

, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

, следовательно, выполнить умножение невозможно, и вообще, такая

запись не имеет смысла

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, и возможно как умножение , так и умножение

Как умножить матрицы?

Начнем с самого простого:

Пример 5:
Умножить матрицу на матрицу
Сразу привожу формулу для каждого случая:

– попытайтесь сразу уловить закономерность.

Умножить матрицу на матрицу

Формула:

В результате получена так называемая нулевая матрица.

Попробуйте самостоятельно выполнить умножение (правильный ответ ).

Обратите внимание, что !Таким образом, переставлять матрицы в произведении нельзя!

Если в задании предложено умножить матрицу на матрицу , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Переходим к матрицам третьего порядка:

Умножить матрицу на матрицу

Формула очень похожа на предыдущие формулы:

А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:

Умножьте матрицу на матрицу

Вот готовое решение, но постарайтесь сначала в него не заглядывать!

Определитель первого порядка равен тому единственному элементу, из которого состоит соответствующая матрица.

Определителем второго порядка называется число .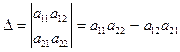

Определителем третьего порядка называется число

Основные свойства определителей:

1. Если строки определителя поменять местами с соответственными столбцами, то значение определителя не изменится.

2. Если переставить две строки (столбца) определителя местами, то значение определителя изменится на противоположное.

3. Если элементы строки (столбца) определителя содержат общий множитель, то его можно вынести за знак определителя.

4. Если две строки (столбца) определителя содержат соответственно пропорциональные элементы, то значение определителя равно нулю.

5. Если к элементам какой-либо строки (столбца) определителя прибавить соответственные элементы другой строки (столбца), умноженные на одно и то же число, то значение определителя не изменится.

Упростив определитель согласно перечисленным свойствам, найдем его значение:

1) вынесем множитель 3 из второй строки за знак определителя;

2) сложим соответственные элементы первой и второй строки;

3) сложим соответственно элементы второго и третьего столбца;

4) вынесем множитель 2 из второго столбца за знак определителя;

5) вынесем множитель 3 из первой строки за знак определителя;

6) вычислим определитель по правилу.

Тема 1.2. Системы линейных уравнений.

Решение систем линейных уравнений методом определителей

(метод Крамера)

Рассмотрим систему трех линейных уравнений с тремя неизвестными: x₁, x₂, x₃:

(коэффициенты a_ij и свободные члены b_i считаются заданными).

Решение: составим определители :

, , , ,

где D называют определителем системы, а определители Dx_iполучены из основного определителя D заменой свободными членами b_i элементов соответствующего столбца.

Особые случаи:

1) если D¹ 0, то система имеет единственное решение;

2) если D = 0, Dx_i¹ 0, то система несовместна;

3) если D = Dx_i= 0, то система либо имеет бесконечное множество решений, либо она решений не имеет.

Решить систему линейных уравнений:

Решение: составим определители D, D_x, D_y, D_zи найдем их значения.

(D¹ 0, следовательно, система имеет единственное решение).

.

.

.

Найдем решение системы:

Раздел 2. Основные понятия и методы математического анализа.

Тема 2.1. Теория пределов.

Предел функции в точке а обозначается .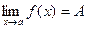

Основные теоремы о пределах

Приведем основные теоремы, на которых основано вычисление пределов:

1.

2.

3.

4.

5.

6.

Техника вычисления пределов

При вычислении предела элементарной функции f(x) приходится сталкиваться с двумя существенно различными типами примеров.

· Функция f(x) определена в предельной точке x = a. Тогда

.

· Функция f(x) в предельной точке x = a не определена или же вычисляется предел функции при x→∞. Тогда вычисление предела требует в каждом случае индивидуального подхода.

Необходимо помнить, что

Более сложными случаями нахождения предела являются такие, когда функция f(x) в точке x = a или при x→∞ представляет собой неопределенность (типа , , , , , , ).

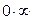
При вычислении пределов при основные теоремы о пределах сохраняют силу и, кроме того, используются правила:

а) чтобы раскрыть неопределенность типа , необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной;

б) чтобы раскрыть неопределенность типа , необходимо числитель и знаменатель дроби разделить на наименьшую степень переменной;

в) чтобы раскрыть неопределенность типа , иногда достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности;

г) чтобы раскрыть неопределенность типа , зависящую от иррациональности, достаточно перевести иррациональность из числителя в знаменатель или из знаменателя в числитель и сократить на множитель, приводящий к неопределенности;

д) чтобы раскрыть неопределенность типа 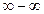, необходимо числитель и знаменатель дроби одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида или .

Вычислить пределы функций:

Пример 1:

Пример 2:

Пример 3:

=

Пример 4:

Пример5:

Тема 2.2. Дифференциальное исчисление.

Определение: Производной функции по аргументу xназывается предел отношения ее приращения к приращению аргумента x, когда приращение аргумента стремится к нулю:

.

Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этотпредел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.

Механический смысл производной:скорость есть первая производная пути по времени, т.е. .

Уравнение касательнойк графику функции в точке :

Уравнение нормали к графику функции в точке :

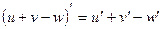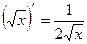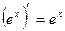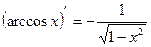Процесс нахождения производных называется дифференцированием функции.

Найти производные функций:

Пример 1:

Решение:

+

Пример2:

Решение:

Пример 3:

Решение:

Дифференциал функции

Определение: Дифференциалом функции y=y(x) называется произведение ее производной на дифференциал независимой переменной: .

Пример 1: Найти дифференциал функции

Решение:

Так как , то .

Дифференцирование сложной функции

, или

Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций: производная сложной функции равна произведению производных функций, ее составляющих.

Производные сложных функций находятся при помощи таблицы:

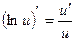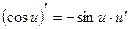Пример 1: Найти производную функции

Решение: =

Пример 2: Найти производную функции

Решение:

=

+

Источник