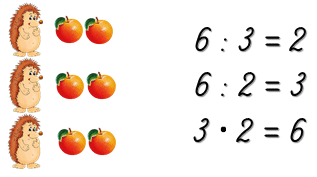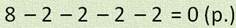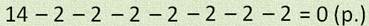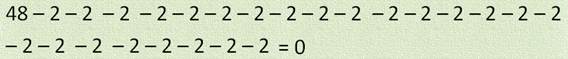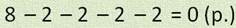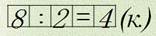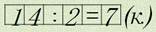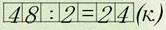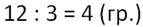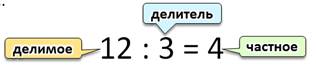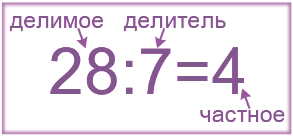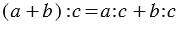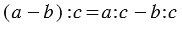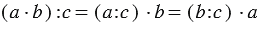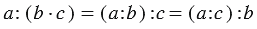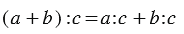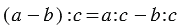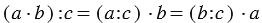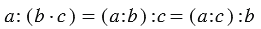Как называют цифры при делении

Деление

В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.

Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.

Как ёжикам поделить между собой яблоки поровну?

Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.

Любой пример на умножение можно представить двумя примерами на деление.

Например, для выражения 6 • 4 = 24 есть два обратных выражения:

24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.

24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.

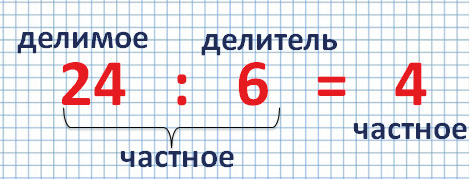
Числа при делении

При делении, как и при другом математическом действии, каждое число имеет свое название.

Число, которое делят, называется делимое.

Число, на которое делят, называется делитель.

Результат деления называется частное.

Чтение числовых выражений

Этот пример можно прочитать по-разному.

Деление на 1

Деление на 0

Деление числа само на себя

Связь деления и умножения

Чётные и нечётные числа

Числа, которые делятся на 2 без остатка, назы­ваются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.

Чётные: 6, 22 44, 60, 74, 82, 96

Нечётные: 7, 13, 21, 37, 45, 97

В несколько раз меньше

Для примера решим задачу:

В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?

Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)

Во сколько раз больше? Во сколько раз меньше?

Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?

Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?

Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.

Поделись с друзьями в социальных сетях:

Источник

Деление

Деление в математике соответствует в жизни делению поровну. Только в математике все участвующие в делении величины имеют определённые названия, что позволяет формулировать правила и соблюдать точность при решении задач.

Как называются числа при делении?

При делении число, которое делят, называют делимое. Число, на которое делят, называют делитель. Результат называют частное. Выражение, составленное из делимого и делителя, называется частное.

30 : 2 = 15
30 — это делимое
2 — это делитель
15 — это частное
30 : 2 — это частное

Как найти неизвестное делимое?

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

Как найти неизвестный делитель?

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

Изменение частного с изменением делимого

При увеличении делимого в x раз частное увеличивается в x раз. При уменьшении делимого в x раз частное уменьшается в x раз.

90 : 2 = 45
30 : 2 = 15
10 : 2 = 5

Изменение частного с изменением делителя

При увеличении делителя в x раз частное уменьшается в x раз. При уменьшении делителя в x раз частное увеличивается в x раз.

90 : 18 = 5
90 : 6 = 15
90 : 2 = 45

Изменение частного с изменением делимого и делителя одновременно

При увеличении делимого в x раз и уменьшении делителя в x раз частное не изменяется. При уменьшении делимого в x раз и увеличении делителя в x раз частное не изменяется.

90 : 18 = 5
30 : 6 = 5
10 : 2 = 5

Деление нуля и деление на ноль

Источник

Математика. 2 класс

Конспект урока

Математика, 2 класс

Урок № 55. Название чисел при делении

Перечень вопросов, рассматриваемых в теме:

1. Как называются числа при делении?

2. Как называется числовое выражение со знаком деление?

Обязательная литература и дополнительная литература:

Теоретический материал для самостоятельного изучения

Запишем равенство, используя необходимое арифметическое действие:

10 яблок разложили на две тарелки поровну.

9 конфет раздали трём детям поровну.

8 тетрадей раздали четырём ученикам поровну.

Для того, чтобы выполнит задание, нам понадобилось действие деление.

Вы уже знаете, как называются числа при сложении и вычитании, недавно вы познакомились с названиями чисел при умножении.

Вы умеете называть выражения со знаками «плюс», «минус», со знаком умножения. Сегодня вы узнаете, как называются числа при делении. Выражение со знаком деления тоже имеет своё название. Хотите узнать? Вперёд!

Числа при делении имеют свои названия.

8 листьев раздали детям, по 2 листа каждому.

4 человека получили листья.

Число, которое делят, называется делимым. 8 – это делимое. Число, на которое делят делимое, называется делитель. 2 – это делитель Результат действия деления называется частным. 4 – это частное. Выражение 8 разделить на 2 тоже называется частным.

Компоненты деления: делимое, делитель, частное.

Найдите частное, если делимое – 6, делитель – 3.

Найдите частное чисел 12 и 6. Проверьте: 12 : 6 = 2

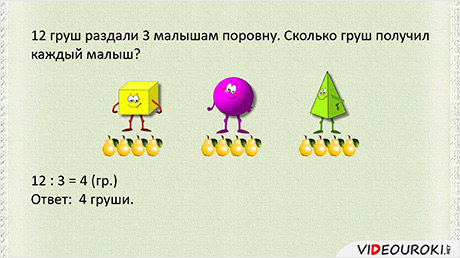
Решим задачу: 12 клубничек раздали 4 детям поровну. По сколько клубничек получил каждый ребёнок?

Для решения задачи выберем действие деление, так как надо узнать, сколько раз по 4 содержится в числе 12.

Ответ: по 3 клубнички получил каждый ребёнок.

Вспомним название чисел при делении. 12 – делимое, 4 – делитель. 3 – частное. 12 : 4 – это частное.

Вывод: компоненты действия деление – делимое, делитель, результат деления – частное.

Ответим на вопросы, поставленные в начале урока.

Число, которое делят, называется делимое.

Число, на которое делят делимое, называется делитель.

Результат деления – частное.

Числа, которые соединены знаком деления, тоже называются частное.

Выполним несколько тренировочных заданий.

1. По рисунку составьте задачи на деление. Запишите решение. Назовите компоненты действия деление.

а) 15 яблок разложили в 3 вазы, в каждую вазу поровну. Сколько яблок положили в одну вазу?

Проверьте: 15 : 3 = 5 (яб.).

15 – делимое. 3 – делитель. 5 – частное. Выражение 15:3 – частное.

б) 15 яблок разложили в вазы, по 5 штук в каждую. Сколько ваз заняты яблоками?

15 – делимое. 5 – делитель. 3 – частное. Выражение 15:5 – частное.

2. Запишите выражение и найдите их значения:

Источник

Конкретный смысл действия деление. Название чисел при делении

Урок 33. Математика 2 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Конкретный смысл действия деление. Название чисел при делении»

Добрый, день, ребята! Как же я по вам соскучился. Я ездил отдыхать к своему родственнику. А Плюс здесь один был. Но теперь настала пора ему отдыхать. Эх, и хорошо ему сейчас на отдыхе.

Посмотрите, как это происходило. Подбежала первая кошка, и получила 2 рыбки, за ней следующая. Ей тоже досталось 2 рыбки, ещё одна кошка получила 2 рыбки. И вот последней прибежала маленькая рыженькая кошечка, которой мы тоже дали 2 рыбки. И вот наше ведёрко опустело.

На следующий день мы поймали уже 14 рыбок. Думали, что покормим кошек, а остальную рыбку пожарим и съедим. Но на этот раз кошек прибежало больше. И мы опять стали каждой давать поровну, по 2 рыбки, до тех пор, пока наше ведёрко вновь не опустело. Сколько же кошек мы накормили в этот раз?

Вот так записали, как мы кормили кошек, с помощью чисел и математических знаков.

М-да, хорошенькая запись получилась. Семь раз выполняется действие вычитания, то есть рыбкой полакомилось 7 кошечек.

Вот посмотрите, как мы кормили кошек в первый день:

А потом мы считали, сколько раз мы давали рыбу кошкам, то есть количество двоек. Вместо такой записи можно выполнить запись гораздо короче. Сначала записываем число, которое показывает, сколько всего было рыбок. Пропускаем клеточку и пишем число, которое показывает, по сколько рыб получила каждая кошка. А между ними ставим знак деления:

Ну а теперь читаем полученную запись: 8 разделить по два получается 4. Значит, мы покормили 4 кошек.

А вот как мы делили между кошками 14 рыб:

Давайте посмотрим, как раздавались груши. Вот 12 груш. Сначала каждому малышу дали по одной груше, потом ещё по одной, ещё по одной и ещё по одной. Груши закончились. Мы распределили 12 груш между 3 малышами поровну, то есть:

Вот так чудесное действие деления. Очень доброе и справедливое. Ведь это действие всегда всё раздаёт поровну. Никому не обидно.

Ну, вот так я отлично и с пользой отдохнул.

И теперь я знаю, что:

· Действие, в котором что-то раздаётся (делится) поровну в математике называется делением.

Второе число показывает, по сколько предметов или на сколько частей делится. И это число называется делитель. Делитель делит.

А ответ показывает, на сколько частей разделили. И поэтому ответ в делении называется частное.

Я очень хочу, чтобы вы любили доброе деление так же, как люблю его я. И никогда не забывали о том, что:

· Действие, в котором что-то раздаётся (делится) поровну в математике называется делением.

Числа в действии деления называются так:

· Делимое, делитель, частное.

· Делимое показывает, какое число делим,

· Делитель показывает, по сколько предметов или на сколько равных частей делится делимое.

· Частное показывает, сколько равных частей получилось.

Ну что же, пришло время прощаться. Мне так понравилась делать добрые дела, что я пойду сейчас угощать конфетами всех обитателей нашего замка. И, конечно, раздавать их буду всем поровну, то есть делить. До свидания, ребята!

Источник

Деление натуральных чисел

Вы уже знакомы с общими понятиями о делении и о том как делить в столбик, рассмотрим более подробно деление натуральных чисел и его свойства.

Рассмотрим задачу:

У Вани 7 кроликов, он собрал для них 28 яблок. Сколько яблок досталось каждому кролику?

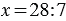
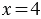
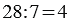
Данное действие записывают так: , или , где:

Частное показывает во сколько раз делимое больше делителя, то есть в нашем примере: 28 больше 7 в 4 раза. Поэтому, если в задаче звучит вопрос «во сколько?», для её решения мы используем деление. При этом не всегда возможно одно число поделить на другое, тогда возникает необходимость деления с остатком.

Из вышесказанного мы можем сделать вывод:

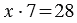
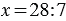
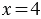
Пример: , следовательно, , то есть .

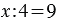
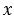
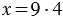
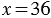
Пример: , по смыслу деления — это произведение 4 и 9, следовательно, , то есть .

Свойства деления

Распределительные свойства:

1. Деление суммы на число:

2. Деление разности на число:

3. Деление произведения на число:

4. Деление числа на произведение:

Действия с единицей и нулем

1. Деление числа на единицу: 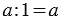то есть, при делении числа на единицу получается само число

2. Деление числа на себя: 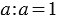, то есть при делении числа, не равного нулю, на само себя получается единица.

3. Деление нуля на число: 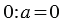, то есть при делении нуля на любое число, не равное нулю, получаем ноль.

НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!

Свойства деления

Распределительные свойства :

1. Деление суммы на число:

а) Мы можем сложить яблоки, которые нашли Маша и Ваня, а потом разделить полученное число на количество кроликов, то есть:

б) Мы можем разделить яблоки, которые собрала Маша, затем разделить яблоки, которые собрал Ваня, а результат сложить:

Мы видим, что в обоих случаях получается один и тот же результат, и можно записать, что: (9+15):3=9:3+15:3.

Вывод: Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно (если это возможно) и полученные частные сложить.

2. Деление разности на число:

Всего трем братьям папа дал 150 рублей. На 72 рубля они купили сестре цветы на день рождения. Сколько рублей осталось у каждого брата?

а) Мы можем из общей суммы вычесть то, что братья потратили, а затем поделить сдачу:

б) Мы можем найти, сколько получил каждый брат, затем посчитать, сколько потрачено каждым из них, а затем вычесть из полученной суммы денег потраченную:

Вывод: Чтобы разделить разность на какое-нибудь число, можно разделить на это число уменьшаемое и вычитаемое отдельно (если это возможно) и из первого частного вычесть второе.

3. Деление произведения на число:

В зооуголке в саду 3 кролика. 12 детей принесли по 6 яблок для кормления питомцев. Сколько яблок досталось каждому кролику?

а) Сначала можем найти общее количество яблок, которые принесли дети, а затем поделить на число кроликов:

б) Мы можем найти сколько детей принесли яблоки одному кролику, а затем умножить на количество принесенных яблок:

б) Мы можем найти по сколько яблок принес 1 ребенок для 1 кролика, а затем умножить на количество детей:

Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: (12 · 6) : 3 = (12 : 3) · 6 = (6 : 3) ·12.

Вывод: Чтобы разделить произведение двух множителей на число, можно разделить на это число любой из множителей (если деление выполнимо) и частное умножить на второй множитель.

4. Деление числа на произведение:

В 4 клетках сидят по 3 кролика. Ваня принес 48 яблок. Сколько яблок досталось каждому кролику?

а) Мы можем найти сколько кроликов всего, а потом поделить яблоки на полученное число:

б) Мы можем найти сколько яблок положат в каждую клетку, а затем, сколько получит яблок каждый кролик:

Если мы рассадим наших кроликов по 4 в три клетки, решая задачу аналогично получим:

Мы видим, что в всех случаях получается один и тот же результат, и можно записать, что: 48 : (4 · 3) = (48 : 4) : 3 = (48 : 3) : 4

Вывод: Чтобы разделить число на произведение двух множителей, можно разделить это число сначала на один из множителей, а затем на второй.

Действия с единицей и нулем

1. Деление числа на единицу:

У Вани один кролик. Он принёс 3 яблока. Сколько яблок достанется кролику?

Будем рассуждать, у Вани всего один кролик, значит все яблоки достанутся ему:

2. Деление числа на себя:

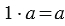
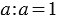
Из свойств умножения мы знаем, что: , а мы знаем, что по смыслу деления можно записать, что: , то есть при делении числа, не равного нулю, на само себя получается единица.

3. Деление нуля на число:

Рассуждая аналогично пункту 2 получаем: 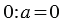, то есть при делении ноля на любое число, не равное нулю, получаем ноль.

Обратите внимание, что НА НОЛЬ ДЕЛИТЬ НЕЛЬЗЯ!

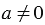
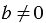
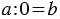
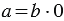
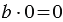
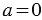
Это легко объяснить следующими рассуждениями: пусть мы взяли карандашей, попробуем разложить их в 0 коробок, и предположим, что получилось по карандашей в каждой коробке: , из смысла деления , в то же время мы знаем из свойств умножения, что: , то есть получаем, что , а это противоречит условию задачи, следовательно делаем вывод, что на ноль делить нельзя.

Поделись с друзьями в социальных сетях:

Источник