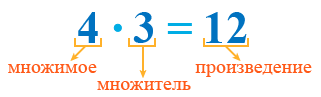Как называется сумма при умножении
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 51. Названия компонентов и результата действия умножения
Перечень вопросов, рассматриваемых в теме:
— Связь умножения со сложением, умение заменять сумму одинаковых слагаемых произведением и произведение – суммой одинаковых слагаемых
Умножение – математическое действие, посредством которого из двух чисел получается новое число, которое содержит слагаемым первое число столько раз, сколько единиц во втором.
Произведение – это результат умножения.
Основная и дополнительная литература по теме урока:
8-е изд. – М.: Просвещение, 2017. – с.54.
7-е изд., дораб. – М.: Просвещение, 2016. – с.46.
Открытые электронные ресурсы по теме урока:
Теоретический материал для самостоятельного изучения
Составьте выражения к рисункам:
2 
Учимся рассуждать. Числа разные: 2 и 3.
К данному рисунку можем составить выражение на сложение: 2 + 3 = 5
Числа одинаковые: 2, 2, 2. К данному рисунку можем составить выражение на умножение:
Компоненты каждого математического действия имеют название.
Компоненты сложения указывают на производимое действие – сложение: первое слагаемое, второе слагаемое, сумма.
Названия носят города и реки,
Вам от рождения фамилия дана.
И каждому числу при умножении
Особенные дали имена.
Так же, как и при сложении и вычитании, числа при умножении тоже имеют свое название.
Первое число при умножении называется первый множитель. Второе число при умножении называется второй множитель. Результат умножения называют произведение.
Зная, как называются числа при умножении, можно использовать эти термины при чтении выражений.
Равенство 5 · 2 = 10 можно прочитать несколькими способами:
— Первый множитель – пять, второй множитель – два, произведение – десять.
— Произведение пяти и двух равно десяти.
— Пять умножить на два, равняется десять.
Рассмотрим задание: слагаемое 12 повторяется 4 раза. Запишите такую сумму в виде произведения.
Назовите первый множитель этого произведения. Что он обозначает?
Первый множитель этого произведения обозначает слагаемое.
Слагаемое 12 повторяется 4 раза.
Назовите второй множитель этого произведения. Что он обозначает? Второй множитель этого произведения обозначает количество слагаемых.
Слагаемое 12 повторяется 4 раза.
Получилась запись: 12+12+12+12=12·4
Помните, что заменить сложение умножением можно там, где находятся суммы одинаковых слагаемых.
1. Запишите пример на умножение там, где это возможно:
Умножение натуральных чисел
Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.
Пример. Во дворе посадили 3 ряда ёлок, по 4 ёлки в каждом ряду. Сколько ёлок посадили во дворе?
Чтобы ответить на этот вопрос, надо найти сумму 3 слагаемых, каждое из которых равно 4.
Складывая 3 раза по 4 ёлки, мы получим общее количество ёлок во всех трёх рядах.
Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.
Для записи умножения используется знак х (косой крест) или · (точка), который ставится между числами. Например:
Эта запись означает, что 4 надо умножить на 3. Справа от записи умножения ставится знак = (равно), после которого записывается полученный результат:
Умножение – это краткая запись сложения одинаковых слагаемых.
Пример. Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести:
Сократим запись, заменив сложение на умножение:
Оба выражения равны:
6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,
но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.
Множимое, множитель и произведение
Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:
4 — это множимое, 3 — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.
Произведение — это число, которое получается в результате умножения. Например, в записи:
12 — это произведение. При этом сама запись 4 · 3 тоже называется произведением.
Множимое и множитель иначе называются множителями или сомножителями.
Проверка умножения
Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.
Умножение
В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.
Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24
Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.
Первое число при умножении показывает, какое слагаемое повторяют несколько раз.
Второе число при умножении показывает, сколько раз повторяют это слагаемое.
Результат умножения показывает, какое число получается.
6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24
Числа при умножении
Результат умножения, или Произведение
Чтение числовых выражений
Этот пример можно прочитать по-разному.
Умножение на 1
4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.
23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.
Умножение на 0
8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.
26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.
Умножение на 10
8 • 10 = 80, потому что число 8 повторяют 10 раз.
15 • 10 = 150, потому что число 15 повторяют 10 раз.
Связь деления и умножения
8 • 3 = 24, потому что 8 повторяют 3 раза.
24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.
24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.
В несколько раз больше
Решим задачу:
В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?
Это значит, что котят было 4 раза по 2.
Заменяем сложение умножением и получаем:
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях:
Умножение
Что такое умножение?
Умножение — это математическое действие, позволяющее по двум известным сомножителям A и B узнать произведение A × B, равное сумме A слагаемых, каждое из которых равно B.
Например, произведение сомножителей 3 и 5 равно сумме трёх пятёрок или сумме пяти троек.
Как называются числа при умножении?
При умножении числа, которые перемножают, называют сомножителями. Результат называют произведением. Выражение, составленное из сомножителей, называют произведением. Например:
Как найти неизвестный сомножитель?
Чтобы найти неизвестный сомножитель, надо произведение разделить на другие сомножители.
Изменение произведения с изменением сомножителей
При увеличении сомножителя в x раз произведение увеличивается в x раз. При уменьшении сомножителя в x раз произведение уменьшается в x раз.
9 × 5 = 45
6 × 5 = 30
3 × 5 = 15
Коэффициент
Коэффициент — это множитель. Например, если яблоки стоят 100 рублей за килограмм, а вишня стоит 200 рублей за килограмм, то чтобы вычислить стоимость яблок и вишни, нужно сложить вес яблок с коэффициентом 100 и вес вишни с коэффициентом 200.
x кг яблок y кг вишни
Стоимость всей покупки равна (100 × x + 200 × y) рублей.
Переместительный закон умножения
Переместительный закон умножения: от перестановки множителей произведение не меняется.
Сомножители под дробной чертой (от которых слева стоит знак деления) переставляются под дробной чертой:
12 × 6 : 2 = 12 × 6 × ( 1 / 2 ) = 12 × ( 1 / 2 ) × 6 = ( 12 : 2 ) × 6
Сочетательный и распределительный законы умножения
Сочетательный закон умножения: произведение многих множителей равно полному произведению неполных произведений.
5 × 25 × 2 × 4 = ( 5 × 2 ) × ( 25 × 4 ) = 1000
Распределительный закон: произведение числа на сумму равно сумме произведений числа на слагаемые.
13 × ( 72 + 28 ) = 13 × 72 + 13 × 28
Произведение числа на разность равно разности произведений числа на уменьшаемое и вычитаемое.
Порядок действий при решении примеров
Действия в скобках выполняются раньше действий за скобками. Умножение и деление выполняются раньше сложения и вычитания.
Как называется сумма при умножении
29. Умножение. Название компонентов при умножении. Свойства умножения
1. Организационный этап
Давайте, ребята, учиться считать,
Чтобы скорей математиком стать.
Ему по плечу любая работа,
Но прежде разучим правила счёта.
Звонок прозвенел. Он позвал на урок.
Пора! Тишина! К нам наука идёт…
2. Этап подготовки учащихся к активному сознательному усвоению знаний
1. Целеполагание
А поможет нам в этом новый герой. Отгадайте загадку и скажите, кто придет сегодня к нам в гости.
2. Устный счёт
Задание 1
Увеличьте 40 на разность чисел 30 и 20. 50
Уменьшите 90 на сумму чисел 10 и 60. 20
Из 85 вычесть сумму чисел 70 и 15. 0
К 42 прибавьте разность чисел 48 и 18. 72
К разности чисел 30 и 5 прибавьте сумму чисел 10 и 40. 75
Из суммы чисел 40 и 50 вычтите разность чисел 36 и 16. 70
Задание 2
Выразите значение в сантиметрах.
26 см = …дм…см 26 см= 2 дм 6 см
1 м = …см 1 м = 100 см
72 см = …дм…см 72 см = 7 дм 2 см
Задание 3
Выразите в часах и минутах.
70 мин =…ч…мин 70 мин = 1 ч 10 мин
1 ч 30 мин=…мин 1 ч 30 мин = 90 мин
Задание 4
Помогите зайке узнать, какой цифры не хватает?
Задание 5
Айболит – непросто доктор,
У него полно хлопот:
На рыбалку он пошёл –
Был отличный, сильный клёв,
Вмиг попались на крючок
Лещ, карась и окунёк,
Три ерша и столько ж щук,
Пескарят двенадцать штук.
Вы вели улову счёт?
Сосчитайте улов доктора Айболита.
Улов доктора – 21 рыба.
1 + 1 + 1 + 3 + 3 + 12 = 21(р.)
Задание 6
Променял Айболит карася
На три пары поросят.
Сколько поросят у доктора? 2 + 2 + 2 = 6 (п.)
Задание 7
Возьмите 9 палочек и сложите фигуру.
Переложите 3 палочки так, чтобы получилось 4 равных треугольника.
3. Этап усвоения новых знаний
Обведите 4 раза по 2 клеточки.
Сколько всего клеточек вы обвели? Восемь.
Какие слагаемые в этой сумме?
Верно, слагаемые одинаковые.
Сколько их? Четыре слагаемых.
Запомните, сложение одинаковых слагаемых можно заменить новым действием – умножением.
Точка – знак умножения. Данное действие называется действием умножения.
Число 2 показывает, какое слагаемое повторяется, и записывается на первом месте. Число 4 показывает, сколько раз оно повторяется, записывается на втором месте.
4. Этап закрепления новых знаний
Задание 1
Рассмотри рисунок и объясни записи.
В каждой корзине по 5 яблок. Чтобы найти, сколько яблок в трех корзинах, нужно сложить 5 три раза.
Сложение одинаковых слагаемых можно заменить умножением.
Читаю: по пять взять 3 раза, получится 15, или 5 умножить на 3, получится 15.
Задание 2
Рассмотрите рисунки, составьте и решите числовые выражения, рассуждая по образцу.
2 мешка по 8 арбузов
8+8=16
8·2=16
7 ваз по 3 розы
3+3+3+3+3+3+3+3=21
3·7=21
3 тарелки по 3 банана
3+3+3=9
3·3=9.
4. Этап закрепления новых знаний
Задание 1
Что обозначает первое число?
Что обозначает второе число?
Чтобы вычислить результат, заменим этот пример на умножение примером на сложение.
Что обозначает число 3?
Верно, 3 раза берём число 10.
Какой пример на сложение получится?
Вычислите сумму
Значит, 10 умножить на 3, получится 30. Записывается – это так.
10 • 3
10 + 10 + 10 = 30
10 • 3 = 30
Причём числа, которые умножают, называются множителями. 10 – первый множитель, 3 второй множитель. Результат умножения называется произведением. Соответственно выражение тоже называется произведением.
4. Этап закрепления новых знаний
Задание 1
Найдите значение выражения.
4 + 4 + 4 = 12
Замените сложение умножением
4 • 3 = 12
Прочитайте запись
Найдите значение выражения
5 + 5 =…
Замените сложение умножением
5 • 2 =…
Задание 2
Найдите значение выражения
Замените сложение умножением
5 + 5 + 5 + 5 + 5 + 5 = 30
5 • 6 = 30
3. Этап усвоения новых знаний
Предлагаю познакомиться со свойством умножения.
Перед вами знакомые школьные парты и ученики.
Сколько детей за первой партой?
За второй?
За третьей?
Сколько детей за тремя партами?
Как узнали? 2 • 3 = 6
Верно, по 2 взяли 3 раза.
Сколько ребят в каждом столбике?
Сколько столбиков?
Как узнать, сколько всего детей? 3 • 2 = 6
Верно, по 3 взяли 2 раза.
Сравните результаты умножения. Как вы думаете, почему они одинаковые?
Молодцы, потому что считали одних и тех же детей, но по-разному. Множители переставили местами, а результат тот же. Сделайте вывод.
От перестановки множителей произведение не изменяется.
Как можно назвать это cвойство умножения? Догадайтесь, вспомнив сложение.
Верно, мы узнали переместительное свойство умножения.
Задание 1
Запишите выражения, используя переместительное свойство умножения.
— Рассмотрите данные выражения, и скажите, какой закономерности подчиняются числа в этих выражениях?
— Запишите это свойство буквами.
а • в = в • а
Запомните, от перестановки множителей результат не меняется.
4. Этап закрепления новых знаний
Задание 1
Используя переместительное свойство умножения, найдите значение второго выражения в каждой паре, зная значение первого.
Задание 2
На одной тарелке 3 яблока. Сколько яблок на четырёх тарелках?
Что известно в задаче?
В задаче даны одинаковые числа. Сколько их?
Что спрашивается в задаче?
Каким действием будем решать задачу?
3 + 3 + 3 + 3 = 12 (ябл.)
Замените сложение умножением и решите задачу.
Задание 3
Назовите фигуру, изображенную на рисунке.
Сколько сторон квадрата достаточно измерить?
Как найти периметр квадрата?
Р = 5 + 5 + 5 + 5 = 20(см)
Можно найти периметр по-другому.
Мы знаем, что сложение одинаковых чисел можно заменить умножением. Р2 · 4 = 8(см)
Задание 4
— Назовите компоненты действия при умножении.
Первый множитель, второй множитель, произведение
— Вычислите, заменяя умножение сложением.
1) 6 • 3
Заменим умножение сложением
6 + 6 + 6 = 18
Значит
6 • 3 = 18
Заменим умножение сложением
5 + 5 + 5 = 15
Значит
5 • 3 = 15
Заменим умножение сложением
2 + 2 + 2 + 2 + 2 = 10
Значит
2 • 5 = 10
Заменим умножение сложением
1 + 1 + 1 + 1 +1 = 5
Значит
1 • 5 = 5
Заменим умножение сложением
1 + 1 + 1 = 3
Значит
1 • 3 = 3
Рассмотрите вычисления и сделайте вывод.
При умножении 1 на любое число в результате получится то число, на которое умножали.
Задание 5
Рассмотрим еще одну особенность умножения.
Замените умножения делением.
Сделайте вывод.
При умножении 0 на любое число получается 0.
Самостоятельная работа
Задание 1
Вычислите, заменяя умножение сложением.
4 + 4 + 4 + 4 = 16
4 • 4 = 16
8 + 8+ 8 = 24
8 • 3 = 24
1 + 1 + 1+ 1 + 1 + 1 = 6
1 • 6 = 6
Проверьте себя и оцените свои успехи.
Задание 2
В одном бидоне 3л молока. Сколько литров молока в шести бидонах?
Сделайте к задаче схематический рисунок и запишите решение задачи сложением и умножением.
3 + 3 + 3 + 3 + 3 + 3= 18 (л)
Ответ: 18 литров.
3 • 6 = 18 (л)
Ответ: 18 литров.
Проверьте себя и оцените свои успехи.
Задание 3
Используя свойство умножения, вставьте пропущенные числа, чтобы равенства стали верными.
Проверьте себя и оцените свои успехи.
Логические задания
Задание 1
К Айболиту пришли лисичка, зайка и волчок. Если зайка, стоящий крайним слева, станет между лисичкой и Айболитом, то доктор Айболит окажется крайним слева. Кто где стоит?
Ответ: Слева направо: зайка, Айболит, лисичка, волчок.
Задание 2
Как из 7 палочек сложить 3 треугольника?
Проверьте, так ли у вас получилось?
5. Этап подведения итогов
С какими новыми математическими действиями познакомились на уроке?
Зайка поднимает табличку «умножение»
Какие слагаемые можно заменить произведением?
Как называется результат умножения?
Волк поднимает табличку «произведение»
Как называются компоненты действия при умножении?
Обезьянка поднимает табличку с названием компонентов действий при умножении.
Сформулируйте свойство умножения.
Айболит поднимает табличку со свойством умножения.
Соберите фразу правильно и вспомните свойства умножения.
Рефлексия
Я узнал
Я научился
Мне было сложно
Всего хорошего. Спасибо за урок.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовиться к ЕГЭ, ОГЭ и другим экзаменам
Подготовиться к поступлению в любой ВУЗ страны