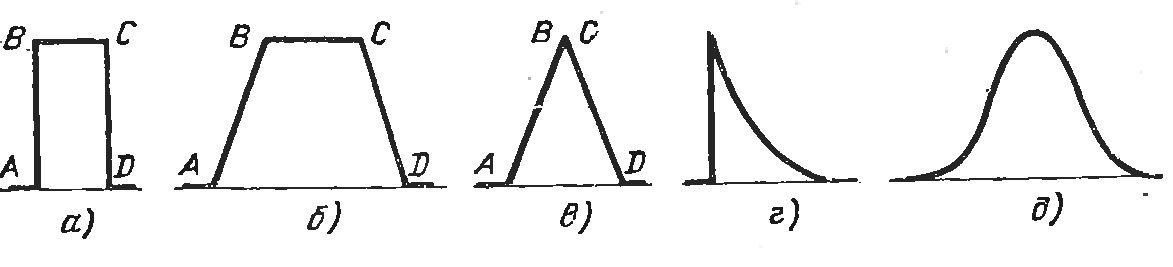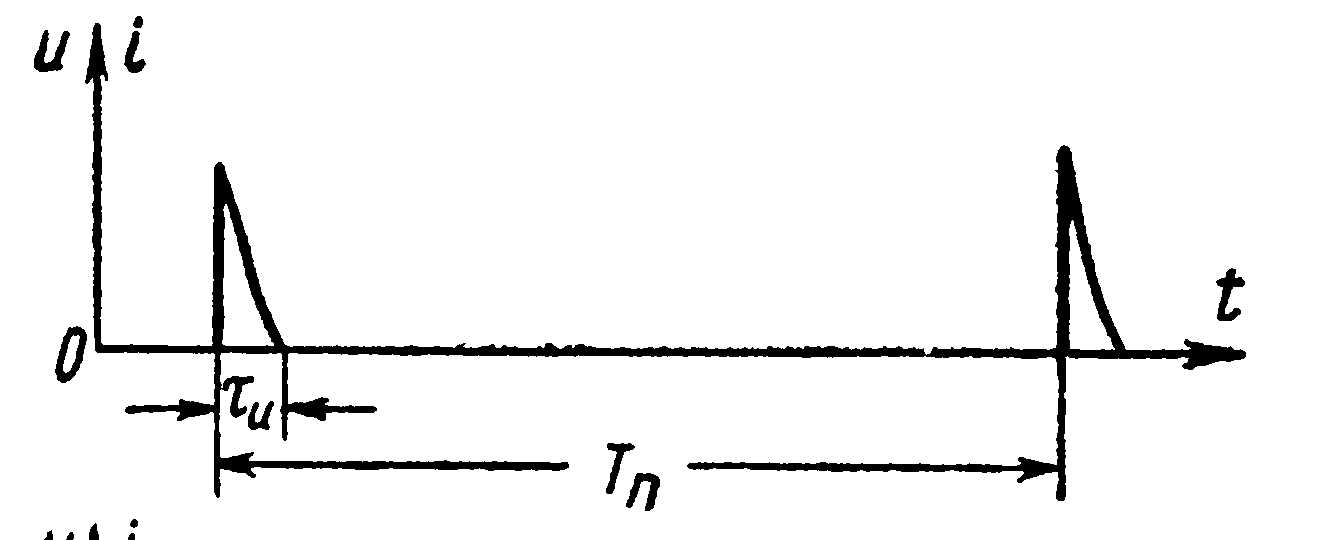Как называется мощность одиночного импульса

Виды импульсов и их параметры.

Под импульсом понимают кратковременное отклонение напряжения или тока от некоторого постоянного уровня, в частности, от нулевого.

Существует два вида импульсов: видеоимпульсы и радиоимпульсы.

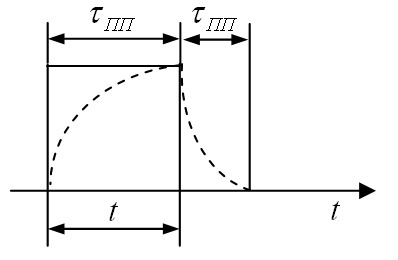
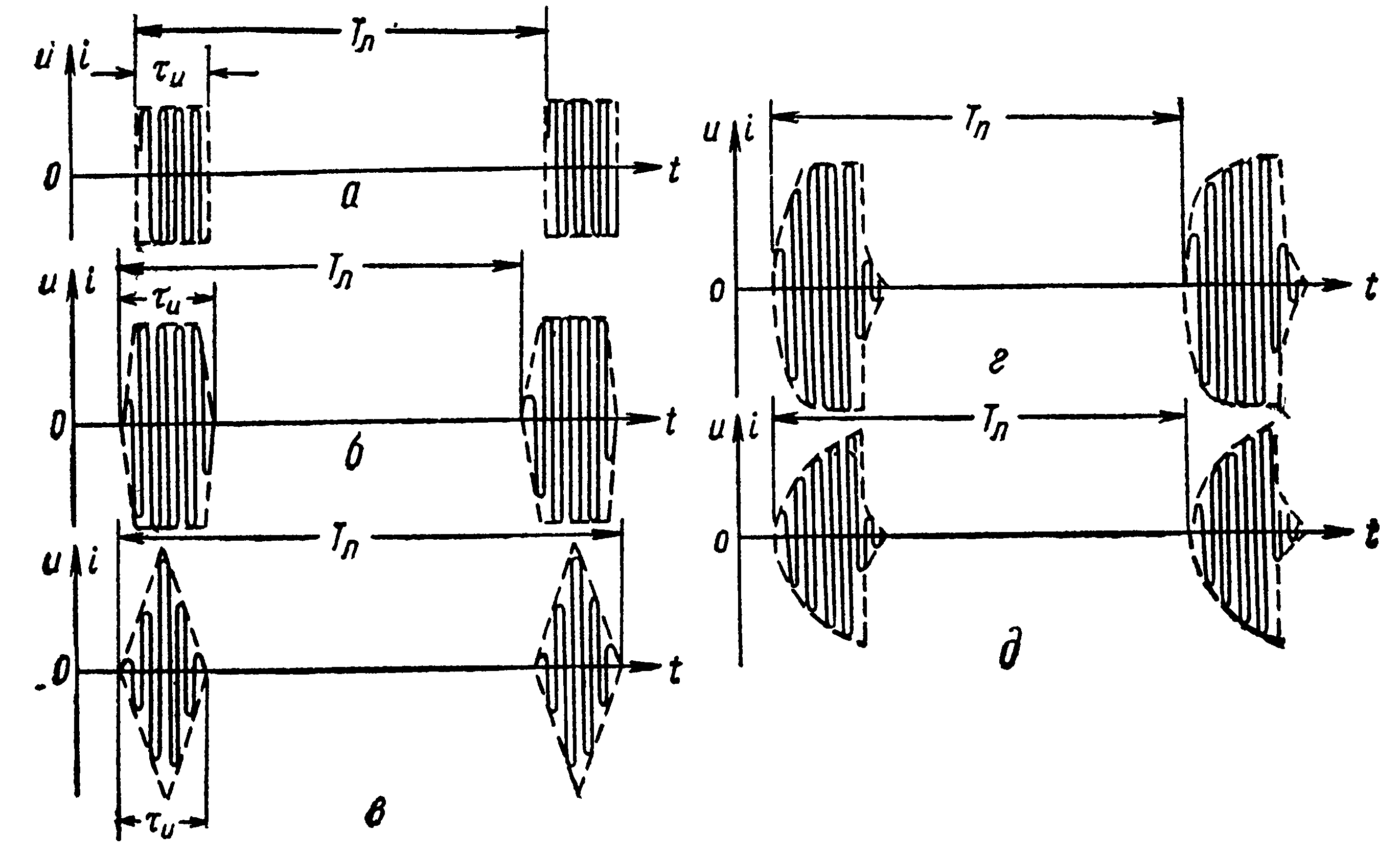
Видеоимпульсы представляют собой кратковременное изменение напряжения или тока в цепи постоянного тока. Видеоимпульсы имеют прямоугольную, трапецеидальную, треугольную, экспоненциальную и колоколообразную формы (рис.15.1).

Рис. 15.1. Идеализированная форма импульсов прямоугольной (а), трапецеидальной (б), треугольной (в), экспоненциальной (г) и колоколо-образной (д) форм.

Следует иметь в виду, что реальные импульсы не имеют формы, строго соответствующей названию. Так, например, прямоугольные импульсы имеют форму, близкую к трапецеидальной, а треугольные – к экспоненциальной.

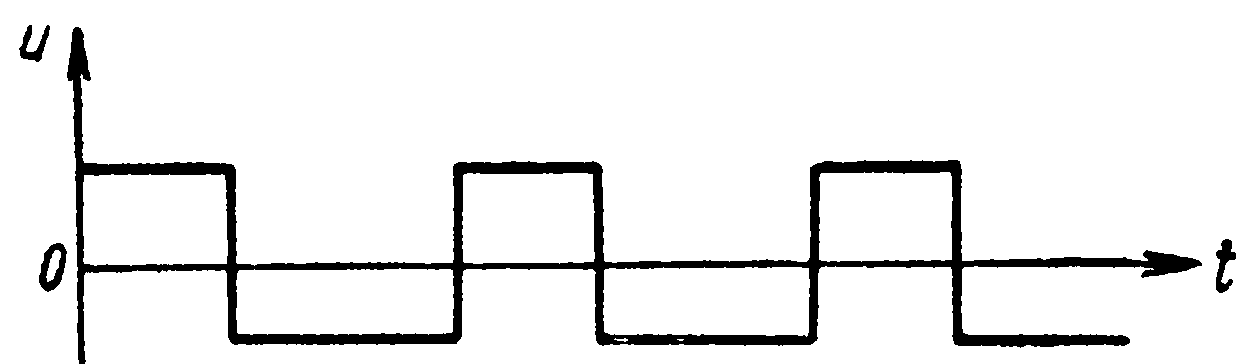
Различают импульсы положительной и отрицательной полярности, а также двухсторонние (разнополярные) импульсы («меандр»).

Рис. 15.2. Двухсторонние (разнополярные) импульсы.

Наиболее часто применяются прямоугольные импульсы.

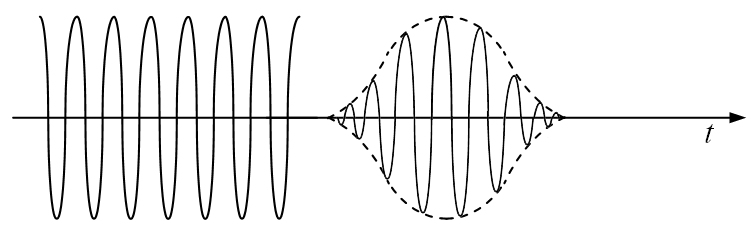
Радиоимпульсы представляют собой кратковременные посылки синусоидального напряжения или тока. Они снимаются с выхода высокочастотного генератора, который управляется (модулируется) видеоимпульсами. Поэтому форма огибающей радиоимпульсов соответ-ствует форме модулирующих видеоимпульсов (рис. 15.3).

Рис. 15.3. Виды радиоимпульсов прямоугольной (а), трапецеидальной (б), треугольной (в), экспоненциальной (г, д) форм.

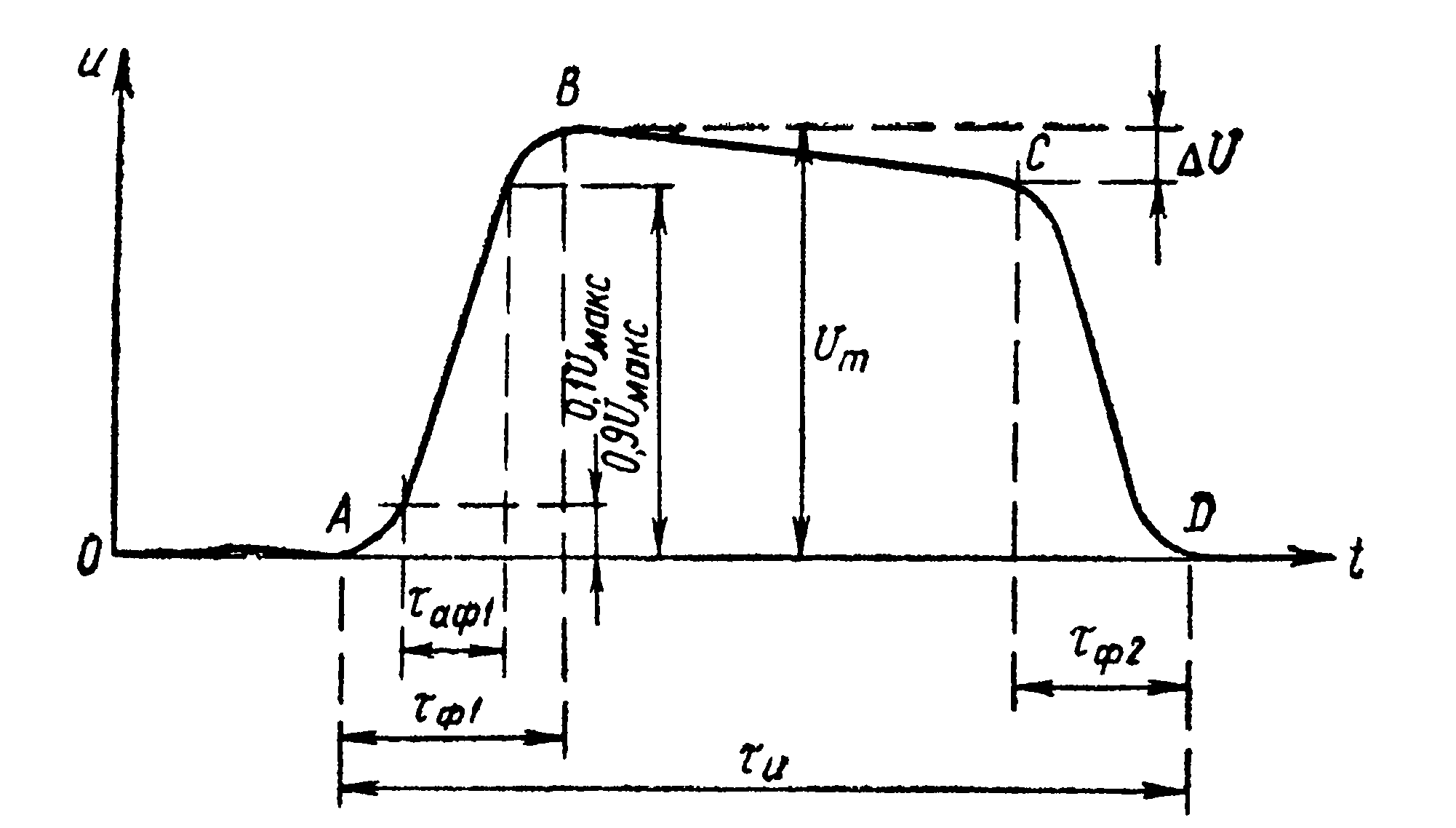
Введём понятие об основных параметрах импульса на примере реального прямоугольного импульса. Как показано на рис. 15.4 такие импульсы имеют передний фронт, срез (задний фронт) и плоскую вершину (участок импульса между фронтами). На рисунке показан также спад плоской вершины (∆U) и как следствие небольшой выброс напряжения. Параметрами реального импульса являются: амплитуда импульса, его длительность и крутизна фронтов, а также мощность в импульсе.

Рис. 15.4. Импульс напряжения прямоугольной формы.

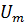
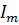
Амплитуда импульса – это наибольшее значение напряжения или тока. Амплитуда напряжения или тока выражается в вольтах, киловольтах, милливольтах, микровольтах или амперах, миллиамперах, микроамперах.

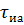
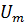
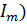
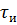
Длительность импульса. За активную длительность импульса принимают промежуток времени, измеренный на уровне, соответствую-щем половине амплитуды. Иногда длительность импульса определяют на уровне 0,1 (0,1 или по основанию импульса. В дальнейшем, если это не оговорено, длительность импульса будет определяться по основанию и обозначаться . Длительность импульса выражается в единицах времени: секундах, миллисекундах, микросекундах и нано-секундах.

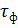
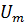
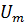
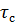
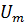
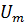
Длительность и крутизна фронта (спада) импульса. Длительность переднего фронта импульса определяется временем нарастания импульса, а длительность среза – временем спада импульса. Наиболее часто пользуются понятием активной длительности фронта , за которую принимают время нарастания импульса от 0,1 до 0,9 . Аналогично, длительность среза – время спада импульса от 0,9 до 0,1 .

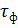
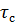
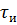
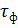
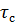
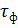
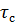
Обычно длительность и составляет единицы процента от . Чем меньше и по сравнению с длительностью импульса, тем больше форма импульса приближается к прямоугольной. Иногда, вместо и фронты импульса характеризуют скоростью нарастания (спада). Эту величину называют крутизной фронта (спада) S 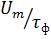и выражают в вольтах в секунду. Для прямоугольного импульса приближённо:

S = (15.1)

Мощность в импульсе. Энергия W импульса отнесённая к его длительности определяет мощность в импульсе:

= (15.2)

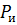
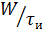
Эта мощность выражается в ваттах, киловаттах, мегаваттах.

2. Параметры импульсных последовательностей.

Импульсы, повторяющиеся через равные промежутки времени, образуют периодическую последовательность. Такая последовательность, параметры которой изменяются в соответствии с передаваемой инфор-мацией, является сигналом.

Кроме параметров, присущих одиночному импульсу, импульсная последовательность характеризуется дополнительными параметрами: периодом повторения импульсов, частотой повторения импульсов, коэффициентом заполнения, скважностью импульсов, а также средним значением мощности импульсного колебания .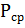

Период и частота повторения импульсов. Промежуток времени 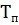между началом двух соседних однополярных импульсов называют периодом повторения (следования) импульсов. Он выражается в единицах времени: секундах, миллисекундах, микросекундах. Величину, обратную периоду повторения, называют частотой повторения (следо-вания) импульсов. Частота повторения импульсов определяет количество периодов в течение одной секунды и выражается в герцах, килогерцах, мегагерцах (рис. 15.5).

Рис. 15.5. Последовательность треугольных импульсов.

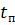
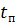
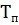
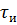
Коэффициент заполнения и скважность импульсов. Часть периода Т занимает пауза – это отрезок времени между окончанием и началом двух соседних импульсов, т.е.:

= — (15.3)

Отношение длительности импульса к периоду повторения называют коэффициентом заполнения:

γ = 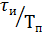(15.4)

Коэффициент заполнения – величина безразмерная меньше единицы.

Величину обратную коэффициенту заполнения называют скважностью импульсов:

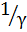
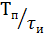
q = = (15.5)

Скважность величина безразмерная больше единицы.

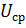
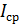
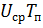
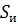
Среднее значение напряжения (тока) импульсного колебания. При определении среднего за период значения напряжения (тока) импульсного колебания ( ), напряжение или ток распределяют рав-номерно на весь период так, чтобы площадь прямоугольника была равна площади импульса .

Так как для прямоугольного импульса:

= (15.6)

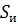
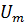
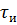
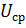
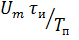
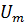
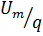
и = = γ = (15.7)

т.е. среднее значение напряжения (тока) прямоугольного импульсного колебания в q раз меньше амплитудного.

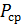
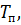
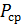
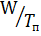
Средняя мощность . Энергия W импульса, отнесённая к периоду импульсов определяет среднюю мощность импульса:

= (15.8)

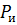
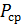
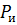
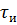
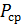
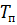
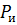
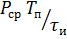
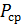
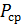
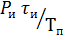
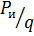
Сравнивая выражения и , получим:

= (15.9)

= = q (15.10)

= = (15.11)

Т.е. средняя мощность и мощность в импульсе отличаются в q раз. Отсюда следует, что мощность в импульсе, которую обеспечивает генератор, может в q раз превосходить среднюю мощность генератора.

Источник

Импульсная и средняя мощность

Рисунок 1. К пояснению понятий «коэффициент заполнения», «импульсная мощность», «средняя мощность»

Рисунок 1. К пояснению понятий «коэффициент заполнения», «импульсная мощность», «средняя мощность»

Импульсная и средняя мощность

Энергия, излучаемая радиолокатором непрерывного излучения может быть легко определена, поскольку передатчик такого радиолокатора работает непрерывно. Однако у импульсного радиолокатора передатчик включается и выключается, чтобы обеспечить получение информации о дальности цели с каждым импульсом. Знать количество энергии, излучаемой в таком случае, важно, поскольку оно связано с мощностью на выходе передатчика, от которой прямо зависит максимальная дальность действия радиолокатора. Чем большую энергию излучает радиолокатор, тем большей будет дальность обнаружения им цели.

Импульсная мощность должна вычисляться чаще, чем средняя мощность. Это вызвано тем, что большинство измерительных средств измеряют среднюю мощность напрямую, как правило, путем оценки нагрева чувствительного элемента датчика. Формула (1) определяет общий подход к расчету импульсной мощности по средней мощности и наоборот.

Поскольку некоторое количество энергии накапливается в модуляторе, система электропитания должна обеспечивать потребляемую мощность передатчика, лишь немного большую, чем средняя излучаемая мощность.

Коэффициент заполнения

Сущность коэффициента заполнения можно пояснить на таком примере (Рисунок 1). Предположим, передатчик работает в течение 1 микросекунды и выключается на 99 микросекунд, затем снова запускается на 1 микросекунду и так далее. В таком случае передатчик работает в течении одной из ста микросекунд или 1/100 всего рабочего времени, то есть его коэффициент заполнения составляет 1/100 или 1 процент. Значение коэффициента заполнения используется при расчетах как импульсной мощности, так и средней мощности радиолокационной системы.

Издатель: Кристиан Вольф, Автор: Андрій Музиченко
Текст доступен на условиях лицензий: GNU Free Documentation License
а также Creative Commons Attribution-Share Alike 3.0 Unported License,
могут применяться дополнительные условия.
(Онлайн с ноября 1998 года)

Источник

Электрические импульсы и их параметры

Под электрическим импульсом понимают отклонение напряжения или тока от некоторого постоянного уровня (в частности, от нулевого), наблюдаемое в течение времени, меньшего или сравнимого с длительностью переходных процессов в схеме.

Как уже было сказано, под переходным процессом понимается всякое резкое изменение установившегося режима в электрической цепи за счёт действия внешних сигналов или переключений внутри самой цепи. Таким образом, переходный процесс – это процесс перехода электрической цепи из одного стационарного состояния в другое. Как бы ни был короток этот переходный процесс, – он всегда конечен во времени. Для цепей, в которых время существования переходного процесса несравненно меньше времени действия внешнего сигнала (напряжения или тока), режим работы считается установившимся, а сам внешний сигнал для такой цепи не является импульсным. Примером этого может служить срабатывание электромагнитного реле.

Когда же длительность действующих в электрической цепи сигналов напряжения или тока становится соизмеримой с длительностью процессов установления, переходный процесс оказывает настолько сильное влияние на форму и параметры этих сигналов, что их нельзя не учитывать. В этом случае бóльшая часть времени воздействия сигнала на электрическую цепь совпадает со временем существования переходного процесса (рис.1.4). Режим работы цепи во время действия такого сигнала будет нестационарным, а воздействие его на электрическую цепь – импульсным.

Рис.1.4. Соотношение между длительностью сигнала и длительностью

а) длительность переходного процесса значительно меньше длительности

сигнала (τ_пп – 9 с).

Характерными участками импульса (рис.1.8), определяющими его форму,

· срез (3 – 4), иногда называемый задним фронтом;

Рис.1.8. Характерные участки импульса

Отдельные участки у импульсов различной формы могут отсутствовать. Следует иметь в виду, что реальные импульсы не имеют формы, строго соответствующей названию. Различают импульсы положительной и отрицательной полярности, а также двусторонние (разнополярные) импульсы

Радиоимпульсами называются импульсы высокочастотных колебаний напряжения или тока обычно синусоидальной формы. Радиоимпульсы не имеют постоянной составляющей. Радиоимпульсы получают модулированием высокочастотных синусоидальных колебаний по амплитуде. При этом амплитудная модуляция производится по закону управляющего видеоимпульса. Формы соответствующих радиоимпульсов, полученных с помощью амплитудной модуляции, показаны на рис. 1.9:

Рис.1.9. Формы радиоимпульсов

Электрические импульсы, следующие друг за другом через равные промежутки времени, называются периодической последовательностью (рис.1.10).

Рис.1.10. Периодическая последовательность импульсов

Периодическая последовательность импульсов характеризуется следующими параметрами:

· Период повторения Т_i – промежуток времени между началом двух соседних однополярных импульсов. Он выражается в секундах (с) или дольных единицах секунды (мс; мкс; нс). Величина, обратная периоду повторения, называется частотой повторения (следования) импульсов. Она определяет количество импульсов, в течение одной секунды и выражается в герцах (Гц), килогерцах (кГц) и т.д.

……………………………….. (1.16)

· Скважность последовательности импульсов – это отношение периода повторения к длительности импульса. Обозначается буквой q:

………………… (1.17)

Скважность – безразмерная величина, которая может изменяться в очень широких пределах, так как длительность импульсов может быть в сотни и даже тысячи раз меньше периода импульсов или, наоборот, занимать большую часть периода.

Величина, обратная скважности, называется коэффициентом заполнения. Эта величина безразмерная, меньшая единицы. Она обозначается буквой γ:

…………………………(1.18)

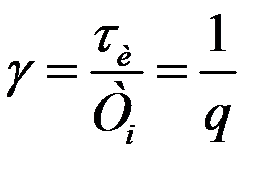
Последовательность импульсов с q = 2 называется «меандром». У такой

последовательности (рис.1.6,е). Если Т_i>> τ_и, то такая последовательность называется радиолокационной.

· Среднее значение (постоянная составляющая) импульсного колебания. При определении среднего за период значения импульсного колебания U_ср (или І_ср) импульс напряжения или тока распределяют равномерно на весь период так, чтобы площадь U_ср ·Т_i была равна площади импульса S_и = U_m · τ_и (рис. 1.10).

Для импульсов любой формы среднее значение определяется из выражения

……………………(1.19),

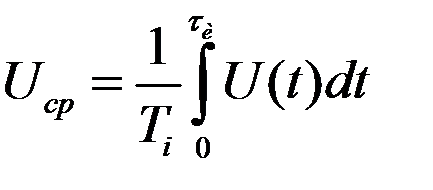
где U(t) – аналитическое выражение формы импульса.

Для периодической последовательности импульсов прямоугольной формы, у которой U(t) = U_m , период повторения Т_i и длительность импульса τ_и, это выражение после подстановки и преобразования принимает вид:

…………………….(1.20).

Из рис. 1.10 видно, что S_и = U_m · τ_и = U_ср·Т_i , откуда следует:

……………(1.21),

где U₀ – называется постоянной составляющей.

Таким образом, среднее значение (постоянная составляющая) напряжения (тока) последовательности прямоугольных импульсов в q раз меньше амплитуды импульса.

· Средняя мощность последовательности импульсов. Энергия импульса W, отнесённая к периоду Т_i , определяет среднюю мощность импульса

…………………………….. (1.22).

Сравнивая выраженияР_и и Р_ср, получим

…………………(1.23)

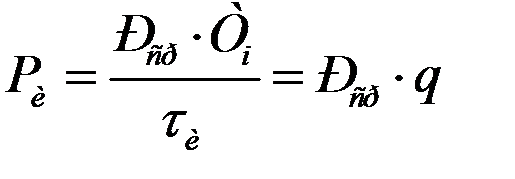
и ……………………. (1.24),

т.е. средняя мощность и мощность в импульсе отличаются в q раз.

Отсюда следует, что мощность в импульсе, которую обеспечивает генератор, может в q раз превосходить среднюю мощность генератора.

Задачи и упражнения

1. Амплитуда импульса равна 11 кВ, длительность импульса 1 мкс. Определить крутизну фронта импульса, если считать длительность фронта равной 20 % длительности импульса.

2. Амплитуда прямоугольных импульсов, имеющих частоту следования 1250 Гц и скважность 2300, равна 11 кВ. Определить крутизну фронта и среза, если считать длительность фронта и среза равной 20 % от длительности импульса.

3. Определить постоянную времени цепи, состоящей из конденсатора ёмкостью 5000 пФ и активного сопротивления 0,5 Мом.

4. Определить постоянную времени цепи, состоящей из индуктивности 20 мГн и активного сопротивления 5 кОм.

5. Определить среднюю мощность радиопередающего устройства РЛС, имеющую следующие параметры: импульсная мощность 800 кВт; длительность зондирующего импульса 3,2 мкс; частота следования зондирующих импульсов 375 Гц.

6. Конденсатор ёмкостью 400 пФ заряжается от источника постоянного напряжения 200 В через сопротивление 0,5 Мом. Определить напряжение на конденсаторе через 600 мкс после начала заряда.

7. К цепи, состоящей из конденсатора ёмкостью 10 пФ и сопротивления 2 Мом, подключён источник постоянного тока с напряжением 50 В. Определить ток в момент включения и через 40 мкс после включения.

8. Конденсатор, заряженный до напряжения 300 В, разряжается через сопротивление 300 Мом. Определить величину разрядного тока через время t = 3τ после начала разряда.

9. Какое потребуется время для заряда конденсатора ёмкостью 100 пФ до напряжения 340 В, если напряжение источника 540 В и сопротивление цепи заряда 100 кОм?

10. Цепь, состоящая из индуктивности 10 мГн и сопротивления 5 кОм, подключена к источнику постоянного напряжения 250 В. Определить ток, протекающий в цепи через 4 мкс после включения.

Глава 2. Формирование импульсов

Линейные и нелинейные цепи

В импульсной технике широко применяются цепи и устройства, формирующие напряжения одной формы из напряжения другой. Такие задачи решаются с помощью линейных и нелинейных элементов.

Элемент, параметры которого (сопротивление, индуктивность, ёмкость) не зависят от величины и направления токов и приложенных напряжений, называется линейным.Цепи, содержащие линейные элементы, называются

линейными.

Свойства линейных цепей:

· Вольт-амперная характеристика (ВАХ) линейной цепи представляет собой прямую линию, т.е. величины токов и напряжений будут связаны между собой линейными уравнениями с постоянными коэффициентами. Пример ВАХ такого вида – закон Ома: .

· Для расчёта (анализа) и синтеза линейных цепей применим принцип суперпозиций (наложения). Смысл принципа суперпозиций заключается в следующем: если к входу линейной цепи приложено синусоидальное напряжение, то напряжение на любом её элементе будет иметь такую же форму. Если же входное напряжение является сложным сигналом (т.е. является суммой гармоник), то на любом элементе линейной цепи сохраняются все гармонические составляющие этого сигнала: иначе говоря, сохраняется форма приложенного к входу напряжения. При этом на выходе линейной цепи изменится только соотношение амплитуд гармоник.

· Линейная цепь не преобразует спектр электрического сигнала. Она может изменить составляющие спектра только по амплитуде и фазе. Это является причиной возникновения линейных искажений.

· Всякая реальная линейная цепь искажает форму сигнала за счёт переходных процессов и конечной ширины полосы пропускания.

Строго говоря, все элементы электрических цепей нелинейны. Однако в определённом интервале изменения переменных величин нелинейность элементов проявляется настолько мало, что практически можно пренебречь ею. Примером может служить усилитель радиочастоты (УРЧ) радиоприёмника, на вход которого подаётся очень малый по амплитуде сигнал от антенны.

Нелинейность входной характеристики транзистора, стоящего в первом каскаде УРЧ, в пределах нескольких микровольт настолько мала, что её просто не учитывают.

Обычно область нелинейного поведения элемента ограничена, а переход к нелинейности может происходить либо постепенно, либо скачкообразно.

Если на вход линейной цепи подать сложный сигнал, который является суммой гармоник разных частот, а линейная цепь содержит частотно-зависимый элемент (L или C), то форма напряжений на её элементах не будет повторять форму входного напряжения. Это объясняется тем, что гармоники входного напряжения по-разному пропускаются такой цепью. В результате прохождения входного сигнала через ёмкости и индуктивности цепи соотношения между гармоническими составляющими на элементах цепи изменяются по амплитуде и фазе по отношению к входному сигналу. В результате соотношения между амплитудами и фазами гармоник на входе цепи и на её выходе не одинаковы. Это свойство положено в основу формирования импульсов с помощью линейных цепей.

Элемент, параметры которого зависят от величины и полярности приложенных напряжений или протекающих токов, называется нелинейным, а цепь, содержащую такие элементы, называют нелинейной.

К нелинейным элементам относятся электровакуумные приборы (ЭВП), полупроводниковые приборы (ППП), работающие на нелинейном участке ВАХ, диоды (вакуумные и полупроводниковые), а также трансформаторы с ферромагнетиками.

Свойства нелинейных цепей:

· Ток, протекающий через нелинейный элемент, не пропорционален приложенному к нему напряжению, т.е. зависимость между напряжением и током (ВАХ) носит нелинейный характер. Примером такой ВАХ служат входные и выходные характеристики ЭВП и ППП.

· Процессы, протекающие в нелинейных цепях, описываются нелинейными уравнениями различного вида, коэффициенты которых зависят от самой функции напряжения (тока) или от её производных, а ВАХ нелинейной цепи имеет вид кривой или ломаной линии. Примером могут служить характеристики диодов, триодов, тиристоров, стабилитронов и др.

· Для нелинейных цепей принцип суперпозиций неприменим. При воздействии внешнего сигнала на нелинейные цепи в них всегда возникают токи, содержащие в своём составе новые частотные составляющие, которых не было во входном сигнале. Это является причиной возникновения

нелинейных искажений, в результате чего сигнал на выходе нелинейной

цепи всегда отличается по форме от входного сигнала.

Дифференцирующие цепи

Для того чтобы получить импульс желаемой формы из заданной формы напряжения с помощью пассивной электрической цепи, необходимо знать формирующие свойства этой цепи. Формирующие свойства характеризуют способность линейной цепи определённым образом изменять форму передаваемого (обрабатываемого) сигнала и полностью определяются видом её частотных и временных характеристик.

В импульсной технике для формирования сигналов широко применяются линейные двух- и четырёхполюсники.

Дифференцирующей называется цепь, на выходе которой напряжение пропорционально первой производной от входного напряжения. Математически это выражается следующей формулой:

………………………. (2.1),

где U_вх – напряжение на входе дифференцирующей цепи;

U_вых – напряжение на выходе дифференцирующей цепи;

k – коэффициент пропорциональности.

Дифференцирующие цепи (ДЦ) применяются для дифференцирования видеоимпульсов. При этом дифференцирующие цепи позволяют производить следующие преобразования:

· укорочение прямоугольных видеоимпульсов и формирование из них остроконечных импульсов, служащих для запуска и синхронизации различных импульсных устройств;

· получение производных по времени от сложных функций. Это используется в измерительной технике, системах авторегулирования и автосопровождения;

· формирование прямоугольных импульсов из пилообразных.

Простейшими дифференцирующими цепями являются ёмкостная (RC)и индуктивная (RL) цепи (рис.2.1):

Рис.2.1. Виды дифференцирующих цепей:

а) ёмкостная ДЦ; б) индуктивная ДЦ

Индуктивная дифференцирующая цепь применяется гораздо реже, чем ёмкостная по чисто практическим соображениям. Дело в том, что для выполнения условия дифференцирования требуется катушка с большой индуктивностью. Такие катушки без железа получаются очень громоздкими и имеют боль-шую паразитную (межвитковую) ёмкость, искажающую результат дифференцирования. Применять же катушки с железом нежелательно, т.к. искажается форма тока из-за нелинейности кривой намагничивания железа, вследствие чего при дифференцировании возникают нелинейные искажения выходного сигнала. Поэтому мы будем рассматривать ёмкостную дифференцирующую цепь.

Покажем, что RC— цепь при определённых условиях становится дифференцирующей.

Известно, что ток, протекающий через ёмкость, определяется выражением:

. (2.2).

В то же время из рис.2.1,а очевидно, что

,

т.к. R и C представляют собой делитель напряжения. Поскольку напряжение

, то .

…………………. (2.3).

Подставив выражение (2.2) в (2.3), получим:

……………… (2.4).

Если выбрать достаточно малую величину R так, чтобы выполнялось условие,

то получим приближённое равенство

……………………….. (2.5).

Это равенство тождественно (2.1).

Выбрать R достаточно малой величины – это значит обеспечить выполнение неравенства

, т.е. ,

где ω_в = 2πf_в – верхняя граничная частота гармоники выходного сигнала, ещё имеющая существенное значение для формы выходного импульса.

Коэффициент пропорциональности в выражении (2.1) k = RC = τ носит название постоянной времени дифференцирующей цепи. Чем резче изменяется подводимое напряжение, тем меньшей величиной τ должна обладать дифференцирующая цепь, чтобы на выходе напряжение было близко по форме к производной от U_вх. Параметр τ = RC имеет размерность времени. Это можно подтвердить тем, что в соответствии с Международной системой единиц (СИ) единица измерения электрического сопротивления

,

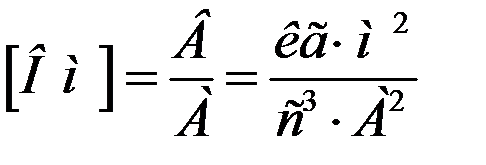
а единица измерения электрической ёмкости

.

Принцип действия дифференцирующей цепи.

Принципиальная схема ёмкостной дифференцирующей цепи изображена на рис.2.2, а эпюры напряжений – на рис.2.3.

Рис.2.2. Принципиальная схема ёмкостной дифференцирующей цепи

Пусть на вход подаётся идеальный прямоугольный импульс, у которого

τ_ф= τ_с = 0, а внутреннее сопротивление источника сигнала R_i = 0.Пусть импульс определяется следующим выражением:

Чем меньше τ цепи, тем быстрее заряжается и разряжается конденсатор и тем меньшую длительность имеют выходные импульсы, тем более остроконечными они становятся и, следовательно, тем точнее дифференцирование. Однако уменьшать τ целесообразно до определённого предела.

Изменение формы импульса на выходе дифференцирующей цепи можно объяснить с точки зрения спектрального анализа.

Каждая гармоника входного импульса делится между R и C. Для гармоник низких частот, определяющих вершину входного импульса, конденсатор представляет большое сопротивление, т.к.

>> R.

Поэтому на выход плоская вершина входного импульса почти не передаётся.

Для высокочастотных составляющих входного импульса, формирующих его фронт и срез,

Источник