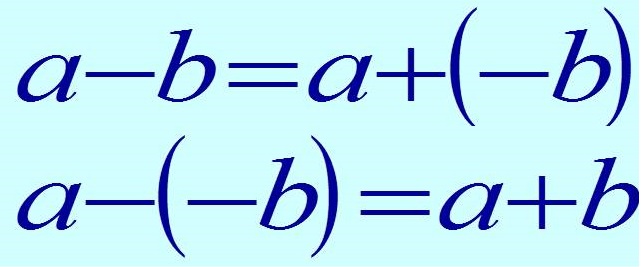Как называется действие с минусом
Действие со знаком «минус»
Последняя бука буква «е»
Ответ на вопрос «Действие со знаком «минус» «, 9 (девять) букв:
вычитание
Альтернативные вопросы в кроссвордах для слова вычитание
Определение слова вычитание в словарях
Толковый словарь русского языка. Д.Н. Ушаков Значение слова в словаре Толковый словарь русского языка. Д.Н. Ушаков
вычитания, ср. (мат.). Одно из четырех арифметических действий, посредством к-рого по двум числам отыскивается третье, дающее в сумме со вторым первое; противоп. сложение. Правило вычитания. Произвести вычитание.
Примеры употребления слова вычитание в литературе.
Двоичное вычитание выполняется просто: инвентируется знак вычитаемого и складываются два числа.
Напомним, что операции инкремента и декремента указателя эквивалентны сложению 1 с указателем или вычитанию 1 из указателя, причем вычисление происходит в элементах массива, на который настроен указатель.
Он быстро выучил их и усвоил простейшие примеры сложения и вычитания, хотя дело затрудняла десятеричная система, изобретенная существами с десятью пальцами на руках и отличная от восьмеричной у тенду, которые имели восемь пальцев.
В число этих операций могут входить сложение, вычитание и умножение функций, сравнение функций, аналогичные операции над функцией и числом, отыскание максимума функций, вычисление неопределенного интеграла, вычисление определенного интеграла от производной двух функций, сдвиг функции по абсциссе и т.
Машина должна иметь устройства, выполняющие основные арифметические операции: сложение, вычитание, умножение и деление.
Источник: библиотека Максима Мошкова
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Сложение и вычитание отрицательных чисел
Давайте вспомним любимую многими сказку «Буратино» и разберем задачу с участием любимых персонажей.
Возвращаемся к решению задачи.
Теперь, правильно запишем и суммируем известные данные.
Рассмотрим еще одно задание.
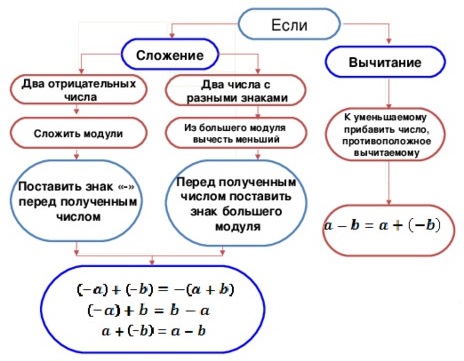
Чтобы вычислить сумму двух значений со знаком «минус», достаточно суммировать их модули, и перед полученной цифрой записать «-».
Запомни! Если складываем два отрицательных числа, то суммируем их модули, а перед результатом сложения записываем «-».
Сложение чисел с разными знаками
Используем рассмотренный алгоритм при выполнении действий.
Суммируем-3 и 10. Для этого:
Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:
Учитывая рассмотренные примеры, можно сказать, что:
любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.
Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.
Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:
Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:
При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.
-150 1 Сложить их модули, а перед результатом поставить знак «плюс»
Правило сложения отрицательных чисел и чисел с разными знаками
Для суммирования двух отрицательных чисел, необходимо:
суммировать их модули;
перед полученной суммой поставить знак «минус».
В данном случае, складываем модули 9 и 6, и перед получившимся натуральным числом 15 ставим знак «-«.
Сложение рациональных или дробных чисел выполняется аналогичным способом:
К 26,35 прибавляем 25,35 (т. е. мы складываем модули), в итоге получаем 51,75 с отрицательным значением. Перед ним ставим знак «минус».
Для суммирования натуральных чисел со знаками «+» и «-», надо:
из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;
перед полученным результатом поставить знак того слагаемого, которое имело большее значение.
61,2 + (-31,5) = + (61,2 — 31,5) = 30,5
Модуль большего числа со знаком «+», соответственно, сумма получилась положительная:
Большее число со знаком «-», поэтому заменяем плюс на минус и получаем отрицательный ответ.
Как вычитать отрицательные и положительные числа
Для нахождения разности противоположных чисел, надо к уменьшаемому прибавить вычитаемое с противоположным знаком, то есть заменить разность суммой.
Наглядно данное действие лучше представить в виде формулы:
То есть любое выражение, содержащее знаки сложения и вычитания, следует решать как сумму чисел.
-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.
Разность выражения будет положительной, если уменьшаемое больше вычитаемого, и отрицательной, если значение модуля уменьшаемого меньше вычитаемого. В случае, когда уменьшаемое и вычитаемое одинаковые, их разность будет равна нулю.
Если нужно отнять отрицательное число, то два знака «минус» подряд дают знак «плюс».
Все вышеперечисленные действия возможно выполнить на калькуляторе. Для этого достаточно ввести сначала модуль числа, потом нажать кнопку изменения знака «+/-».
Заключение
Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма.
Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
Действие сложение. Знак +
Название компонентов действия сложения. Переместительное свойство сложения
Добрый день! Готов к новому уроку? Сегодня у нас будет очень важное занятие. Мы получим самые драгоценные и сокровенные знания. Без этих знаний невозможно существование науки математики!
В таком сложном деле нам нужны помощники. Мы их найдем в сказочном лесу.
— Догадался? В этом лесу живут настоящие профессионалы по поиску драгоценностей и сокровищ. Это сказочные гномики.
Посмотри на них, какие они веселые и доброжелательные. Гномики улыбаются тебе и желают хорошего настроения на весь урок. Улыбнись им в ответ и давай приступим к занятию.
Гномики целый день работали в шахте. Они искали драгоценные камни.
Посмотри, сколько камней собрал гном Том и гном Тим. Посчитай.
Гном Том собрал 4 камня.
А гном Тим собрал 3 камня.
Чтобы не нести эту тяжесть в руках, они сложили все свои камни в тачку.
Теперь в тачке лежат и камни, которые собрал Том, и камни, которые собрал Тим. Давай-ка мы их все достанем и пересчитаем.
В тачке оказалось 7 камней.
Ого, как много! Как ты думаешь, почему?
Верно, потому что в тачку сложили камни оба гномика. А это всегда будет больше, чем у каждого по отдельности.
Итак, что сделали гномики?
Точно, они сложили свои камни вместе. В математике такое действие тоже называется сложение. Его суть в том, что элементы двух множеств объединяются в одно целое.
Смотри, множество камней Тома и множество камней Тима объединились в тачке в одно множество. При этом в объединенном множестве количество элементов становится больше.
Чтобы узнать результат сложения чисел, нужно пересчитать все элементы и первого, и второго множества вместе.
Гномики сложили камни вместе. А какие еще действия приводят к тому, что предметов становится больше?
Таких действий довольно много. Например, если в добавок к тому, что уже есть, кто-то:
Любое действие, которое ведет к увеличению количества предметов, подразумевает выполнение действия сложения. Часто это действие еще называют «прибавление».
Чтобы записать действие сложение в виде математического выражения, используется специальный знак. Знак сложения выглядит так.
Посмотри, в этом знаке тоже произошло объединение: две палочки соединились в одно целое. Этот знак называется «плюс».
Посмотри, как знак «плюс» пишется в тетради.
Порядок написания следующий.
Потренируйся писать знак плюс в тетради.
Теперь разберемся, как именно надо составлять математическое выражение, описывающее действие сложения. Давай вспомним, что было сначала.
Том собрал 4 камня и Тим собрал 3 камня.
Они вместе высыпали свои камни в тачку, т.е. объединили их. Поэтому мы ставим между числами знак «+».
В результате объединения все камни оказались в тачке. Мы их все пересчитали – в тачке 7 камней. Их ровно столько, сколько было у обоих гномиков вместе. Поэтому между левой и правой частью выражения нужно поставить знак равенства «=».
В тетради надо записать так.
Теперь я расскажу, как называются компоненты действия сложения. Числа, которые обозначают количество элементов в каждом отдельном множестве, называются слагаемые. А число, которое обозначает результат, полученный при объединении этих множеств, называется сумма.
Поскольку левая сторона записи равна правой, то и само выражение тоже называют «сумма». Читают так «сумма чисел 4 и 3».
Поэтому, когда говорят «найди сумму», нужно выполнить действие сложение.
Итак, наше выражение можно прочитать несколькими способами:
Идем дальше. Нам нужно выучить очень важное правило для действия сложения. Давай вернемся к нашим гномикам. Ты же помнишь, что каждый из них положил свои камни в тачку и потом мы их посчитали вместе, т.е. нашли сумму. Как ты думаешь, кто из гномиков первый положил камушки в тачку?
Мы записали, что первое слагаемое четыре. Получается, что первым был гномик Том, а потом гномик Тим.
Теперь давай представим, что порядок был другой. Сначала в тачку положил свои камушки Тим, а потом Том. Значит первое слагаемое – это три, а второе – четыре. Изменится ли от этого общее количество камней в тачке, т.е. наша сумма?
Теперь в тачке три камня Тима и четыре камня Тома. Посчитай их вместе.
Всего камней семь. Ровно столько же, сколько был и первый раз.
Получается, что не важно, кто из гномиков положил камушки первый, а кто второй. Их общее количество не меняется. Значит, сумма не меняется.
Посмотри. И четыре плюс три будет семь, и три плюс четыре тоже будет семь.
В математике это называется переместительное свойство сложения. Оно звучит так: от перестановки слагаемых местами сумма не изменяется. Запишем.
Это переместительное свойство очень пригодится тебе при изучении таблиц сложения. Запомни его!
Чтобы закрепить все, что мы узнали о действии сложения, потренируемся составлять примеры по картинкам.
Посчитай, сколько синих фигур на картинке. Запиши.
Теперь посчитай красные фигуры и запиши.
Нам нужно посчитать их вместе. Это подразумевает объединение всех фигур. А значит, надо выполнить действие сложение. Поэтому поставим между нашими числами знак «плюс».
3 + 2
Теперь нужно пересчитать ВСЕ фигуры ВМЕСТЕ. Сколько у тебя получится?
У меня вышло 5. Уверена, у тебя тоже. Запишем это, поставив сначала знак равенства.
3 + 2 = 5
Вот и все. Ничего сложного.
Теперь рассмотрим, как нужно решать примеры на сложение. Давай прочитаем это выражение.
2 + 4
Можно так «два плюс четыре».
Чтобы найти результат, нужно следовать алгоритму выполнения действия сложения.
Это знак «плюс», значит нужно объединить, посчитать все вместе.
2 + 4 = 6
Вот и все. Теперь ты знаешь, что такое действие сложение, как называются компоненты сложения, а также как составлять и решать примеры, в которых нужно выполнить это действие.
Действие вычитание. Знак-
Название компонентов действия вычитания
Давай продолжим раскрывать тайны науки математики. Ведь есть еще одно очень важное математическое действие, с которым нам обязательно нужно познакомиться.
Итак, гномики закончили свою работу и возвращаются домой.
Дома их ждет Белоснежка.
Она приготовила для гномиков угощение – испекла пирожные. Посчитай, сколько их получилось.
У тебя тоже получилось девять пирожных? Значит, ты посчитал правильно!
Когда гномики пришли домой, каждый из них съел по пирожному. Помнишь, сколько было гномов у Белоснежки? Точно, семь. Они съели столько же пирожных, т.е. тоже семь.
Давай зачеркнем съеденные пирожные.
Мы видим, что осталось совсем мало – всего два пирожных. Наверное, они достанутся Белоснежке.
В математике действие, которое ведет к уменьшению количества предметов, называется вычитание. Его смысл в следующем. Из целого множества удаляется его часть. В итоге остается меньше элементов, чем их было в целом множестве.
Чтобы узнать результат действия вычитания, нужно пересчитать элементы, которые остались.
Давай подумаем, в каких случаях предметов станет меньше. Пирожных стало меньше, потому что гномики съели часть из них. Еще могут быть такие ситуации:
Для того, чтобы записать действие вычитания в виде математического выражения используют специальный знак. Знак вычитания выглядит так.
Он называется «минус».
В тетради знак «минус» пишется так.
Порядок написания знака «минус» следующий.
Потренируйся писать знак «минус» в тетради.
А теперь я расскажу, как составлять математическое выражение, которое описывает действие вычитание.
Вспомни, сколько пирожных было сначала?
Правильно, 9. Запиши.
Гномики съели пирожные и их стало меньше, поэтому ставим знак «минус».
Они съели 7 пирожных. Запишем это число.
9 – 7
Ставим знак равенства и запишем количество пирожных, которые остались. Их оставалось 2.
9 – 7 = 2
В тетради запись выглядит так.
Названия компонентов действия вычитания запомнить довольно легко.
Левая сторона этого выражения тоже называется разность.
Если в задании говорится, что нужно «найти разность чисел», значит, следует составить математическое выражение с действием вычитания.
Такое выражение можно прочитать по-разному.
Закрепим все, что ты узнал о действии вычитания и составим математическое выражение по такой картинке.
Посмотри, сколько всего было шариков у гномика сначала? Запиши.
Что случилось с некоторыми шариками? Сколько таких шаров?
Верно, два шарика сдулись и у гномика шариков осталось меньше. Значит нужно написать «минус два».
5 – 2
Ставим знак равенства и пересчитаем, сколько осталось целых шариков.
5 – 2 = 3
Вот мы и составили выражение.
А теперь разберемся, как нужно решать примеры на вычитание. Например, посчитаем, сколько будет:
Назови уменьшаемое. Выложи столько же кружочков. Их должно быть 6.
Теперь назови вычитаемое. Убери (отодвинь, зачеркни) четыре кружочка.
Пересчитай кружочки, которые остались, и ты узнаешь ответ. Запиши его после знака равенства.
6 – 4 = 2
Мы решили пример на вычитание. Теперь ты знаешь, что обозначает это математическое действие, как называются компоненты вычитания, и как нужно составлять и решать математические выражения с действием вычитания.
Взаимосвязь между действием сложения и действием вычитания
Итак, ты выучил два математических действия: сложение и вычитание. Одно из них используется при объединении предметов в единое множество, а другое при удалении из целого множества его части.
Ты вспомнил, что обозначает каждое действие?
Эти действия связаны между собой, но имеют противоположное значение. При сложении мы получаем больший результат, а при вычитании предметов становится меньше. Вот, например, представь, что у тебя было несколько конфет и тебе дадут еще пару штук. Что получится?
Правильно, у тебя конфет станет больше.
А если ты съешь несколько конфет? Что у тебя останется?
Правильно, у тебя останется меньше конфет.
А теперь давай проверим, какая именно взаимосвязь между действиями сложения и вычитания. Разберем одну ситуацию и составим по ней математическое выражение.
У Белоснежки День рождения. Гномики решили устроить для нее праздник. Посчитай, сколько их всех на картинке.
К Белоснежке на День рождения пришли зверята. Посчитай, сколько их.
Подумай, какое действие мы должны использовать, чтобы составить выражение?
Ну конечно, действие сложение. Ведь теперь их всех вместе стало больше.
Было три, пришло еще пять. Посчитай, сколько теперь всех вместе.
Запишем в виде выражения.
3 + 5 = 8
3 – это первое слагаемое, оно показывает, сколько элементов было в первом множестве.
5 – это второе слагаемое, оно показывает, сколько элементов было во втором множестве.
8 – это сумма, она обозначает количество элементов в общем множестве.
Теперь на полянке и гномики с Белоснежкой (это наше первое множество), и зверята (это второе множество). Они все вместе.
Получается, что на празднике веселились 8 друзей. Когда праздник закончился, зверята ушли домой. Как ты думаешь, какое математическое действие надо использовать в этом случае?
Правильно, действие вычитание. Ведь зверята ушли и на полянке останется меньше друзей.
Итак, 5 зверят ушло. Кто остался? Сколько их?
Верно, остались гномики с Белоснежкой. Их 3.
Составим математическое выражение.
8 – 5 = 3
Мы видим, что если из общего множества (суммы) убрать элементы второго множества (второе слагаемое), то останутся только элементы первого множества (первое слагаемое).
А если было наоборот, из 8 друзей первыми с полянки ушли гномики с Белоснежкой (их 3). Кто на ней останется?
Правильно, останутся зверята. Их 5.
Посмотри, как это запишем.
8 – 3 = 5
Теперь мы из общего множества (суммы) убрали элементы первого множества (первое слагаемое) и остались только элементы второго множества (второе слагаемое).
Итак, у нас получается, что мы при сложении два множества объединяем в одно целое. А если из этого общего множества убрать какое-то одно из составляющих множеств, то останется другое.
В математике это правило взаимосвязи между компонентами сложения звучит так: если из суммы вычесть одно слагаемое, то получим другое слагаемое.
Мы видим, что в примере на сложение есть два слагаемых. Поэтому можно сделать следующий вывод: из одного математического выражения с действием сложения можно составить два выражения с действием вычитания.
8 – 3 = 5
8 – 5 = 3
Это очень важное правило, которое поможет тебе в дальнейшем быстро и легко учить таблицы вычитания.
А на сегодня все. Гномики помогли нам получить очень важные и ценные знания. Нужно обязательно поблагодарить их за это.
В материалах урока использованы кадры из а/ф «Белоснежка и семь гномов», 1937
Свойства сложения и вычитания
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Свойства сложения
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число
Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.
Слагаемые — это числа, единицы которых складываются.
Сумма — это число, которое получается в результате сложения.
Рассмотрим пример 2 + 5 = 7, в котором:
При этом саму запись (2 + 5) можно тоже назвать суммой.
Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.
Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.
Свойства вычитания
Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.
Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.
Уменьшаемое — это число, из которого вычитают.
Вычитаемое — это число, которое вычитают.
Разность — это число, которое получается в результате вычитания.