Как наглядно иллюстрируют соотношение между множествами
Лекция 2. Отношение между множествами.
Лекция 2. Отношения между множествами.
Между двумя множествами существует пять видов отношений.
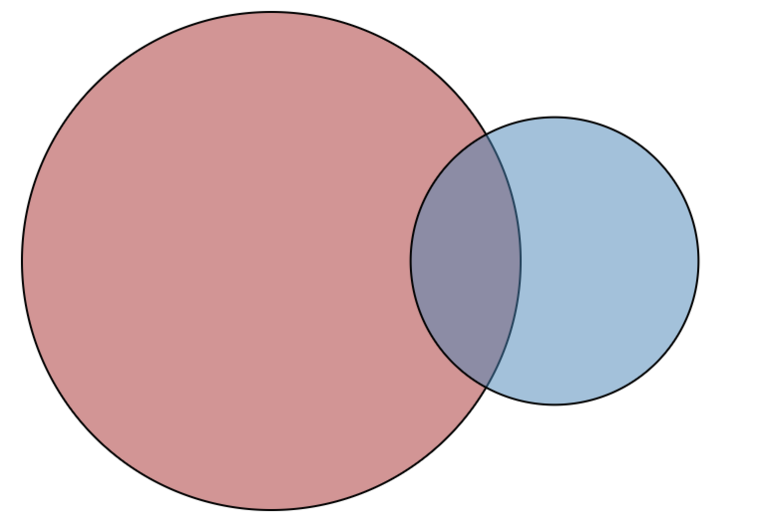
Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество является подмножеством любого множества. Само множество является подмножеством самого себя. (пишут В ⊂ А)
Если множества А и В состоят из одних и тех же элементов, то они называются равными.
Существует пять случаев отношений между двумя множествами. Их можно наглядно представить при помощи особых чертежей, которые называются кругами или диаграммами Эйлера-Венна.
Разбиение множества на классы называют классификацией.
Если элементы множества обладают двумя независимыми свойствами, то все множество разбивается на 4 класса. Например, на множестве натуральных чисел заданы два свойства: «быть кратным 2» и «быть кратным 3». При помощи этих свойств в множестве N можно выделить два подмножества А и В. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 6). Тогда в первый класс войдут числа, кратные 2 и 3, во второй – кратные 2, но не кратные 3, в третий – кратные 3, но не кратные 2, в четвертый – не кратные 2 и не кратные 3.
П р и м е р 1. Пусть Х – множество четырехугольников, А, В и С – его подмножества. Можно ли говорить о разбиении множества Х на классы А, В и С, если:
а) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, противоположные стороны которых не параллельны;
б) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, имеющих прямой угол?
Р е ш е н и е. а) Множества А, В и С попарно не пересекаются. Действительно, если у четырехугольника, противоположные стороны не параллельны, то он не может быть параллелограммом или трапецией. В параллелограмме противоположные стороны попарно параллельны, поэтому он не может принадлежать ни множеству В, ни множеству С. Наконец, в трапеции две противоположные стороны параллельны, а две другие не параллельны, поэтому трапеция не может принадлежать ни множеству А, ни множеству С. Объединение множеств А, В и С даст все множество четырехугольников. Условия классификации выполнены, множество всех четырехугольников можно разбить на параллелограммы, трапеции и четырехугольники, противоположные стороны которых не параллельны.
б) Множества А и В не пересекаются, но множества А и С имеют общие элементы, примером может служить прямоугольник, множества В и С тоже пересекаются: общим элементом является прямоугольная трапеция. Следовательно, нарушено первое условие классификации. Не выполняется и второе условие, так как некоторые четырехугольники не попадают ни в одно из подмножеств А, В или С, таким является четырехугольник с непараллельными сторонами и непрямыми углами. В этом случае множество Х на классы А, В и С не разбивается.
Задания для самостоятельной работы по теме:
Приведите примеры множеств А, В, С, если отношения между ними таковы:
2. Образуйте все подмножества множества букв в слове «крот». Сколько подмножеств получилось?
5. Имеется множество блоков, различающихся по цвету (красные, желтые, зеленые), форме (круглые, треугольные, прямоугольные), размеру (большие, маленькие). На сколько классов разбивается множество, если в нем выделены подмножества: А – круглые блоки, В – зеленые блоки, С – маленькие блоки? Сделайте диаграмму Эйлера и охарактеризуйте каждый класс.
6. Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) А ∩В=Ø
7. Пусть Х= < x 


А – подмножество всех четных чисел;
В – подмножество всех нечетных чисел;
С – подмножество всех чисел, кратных 3;
D – подмножество всех чисел, являющихся квадратами;
Отношения между множествами.



Вместо кругов Эйлера определенные множества изображают любые другие замкнутые фигуры, и такую иллюстрацию называют диаграммами Венна.
Для рассуждений, связанных с множествами, будем использовать язык диаграмм Эйлера Венна.
Область, представляющую то подмножество, которое нас интересует, отметим штрихами.
Если множества А и В не имеют общих элементов, то их называют непересекающимися. Диаграммы Эйлера-Венна для этого случая представлены на рисунке.
Пример 1.6. Приведем примеры множеств, находящихся диаграммах.
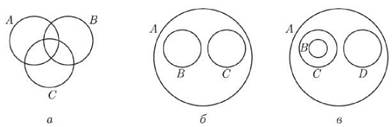 |
Решение. 1. Для случая, представленного на рисунке а, можно рассмотреть:
2.Примерами множеств, представленных на диаграмме б, могут служить:
3.Диаграммы Эйлера-Венна будут иметь вид, представленный на рисунке в, если, например:
Пример 1.7. О каких множествах говорится в утверждении «Все студенты нашей группы участвовали в праздничной демонстрации»? Выделите эти множества и установите, в каких отношениях они находятся.
4. Операции над множествами.

5. Свойства операций над множествами.
Множества в математике
Диаграммы Венна помогают показать связь теории множеств и логических операций. Круги Эйлера, множества чисел и других предметов тесно связаны. Под множеством понимается совокупность каких-то объектов, называемых элементами. В множества можно объединять объекты с общим признаком. Например, множество студентов второго курса университета или множество статей, написанных одним учёным. Можно выделить три вида таких математических объектов:
Группа элементов, составляющая множество, входящее в другое, более обширное множество называется подмножеством. Такое отношение получается между множеством действительных чисел и входящим в его состав подмножеством натуральных чисел.
В курсах информатики и обычно изучаются такие темы как «Введение в математическую логику» и «Поиск информации в Интернет». При решении задач по этим темам помощь оказывают диаграммы Венна. Для их построения можно использовать онлайн-калькулятор. Обозначения операций над множествами, которым должны соответствовать обозначения в калькуляторе:
Калькулятор выдаёт результат и подробное решение с правильным порядком операций при подстановке конкретных множеств.
Кольцом в теории множеств называют непустую систему R, замкнутую относительно пересечения и симметрической разности, то есть при пересечении или операции симметрической разности любых двух множеств обязательно получается множество, входящее в R. Это означает, что для любых элементов A, B из кольца элементы A∩B и A∆B будут лежать в кольце.
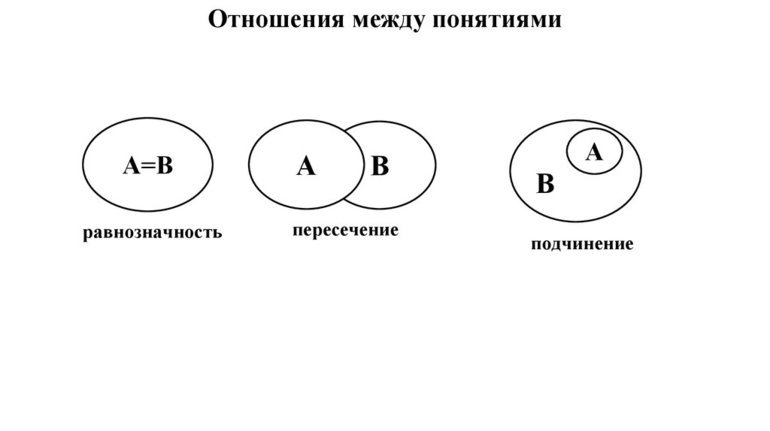
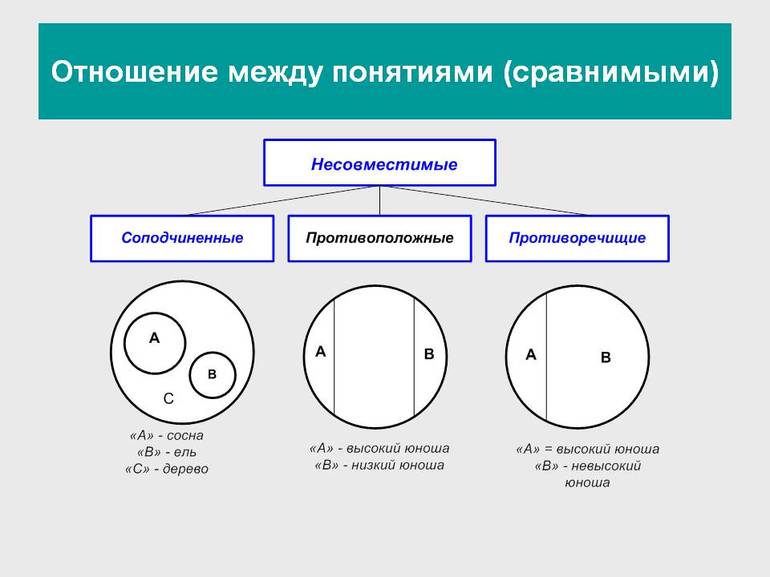
Отношения между понятиями
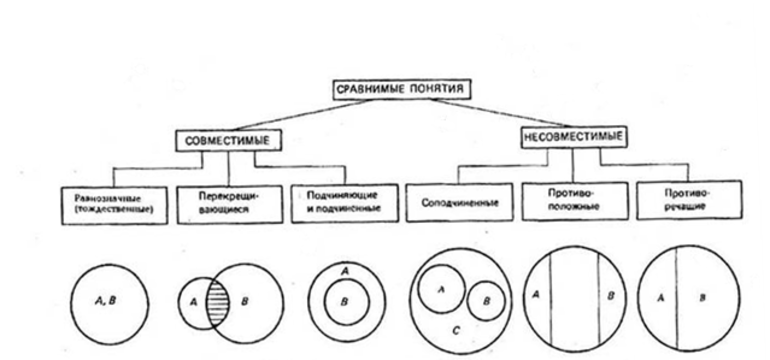
Логические операции, разрешающие доказывать утверждения и делать выводы, основаны на связях и отношениях разных понятий. При классификации понятия делятся на сравнимые, между которыми существуют логические связи и отношения, и несравнимые, которые не имеют связей. К несравнимым относятся, например, «машина» и «квадрат», «озеро» и «клетка». У них нет общих элементов и их нельзя сравнивать.
Рисунок 1
Сравнимые понятия подразделяются на совместимые и несовместимые. Совместимые понятия отличаются тем, что имеют хотя бы один общий элемент:
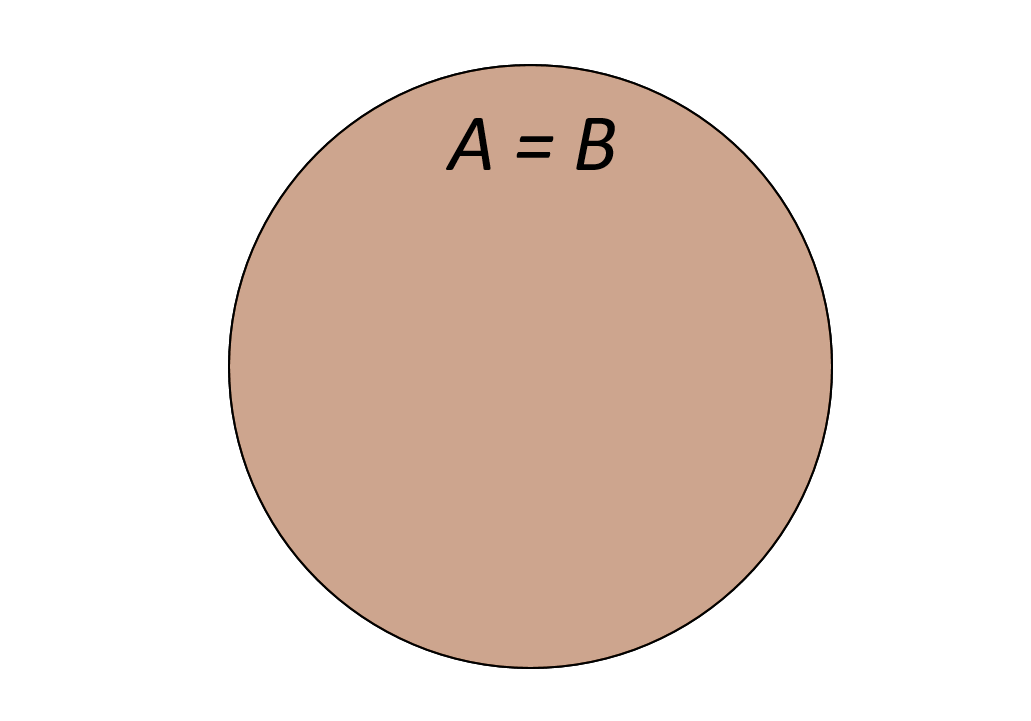
У равнозначных понятий объёмы полностью совпадают. Например, А — писатель Чехов, В — автор пьесы «Вишнёвый сад». Графически тождественность можно представить как два круга, слившиеся в один (Рисунок 1).
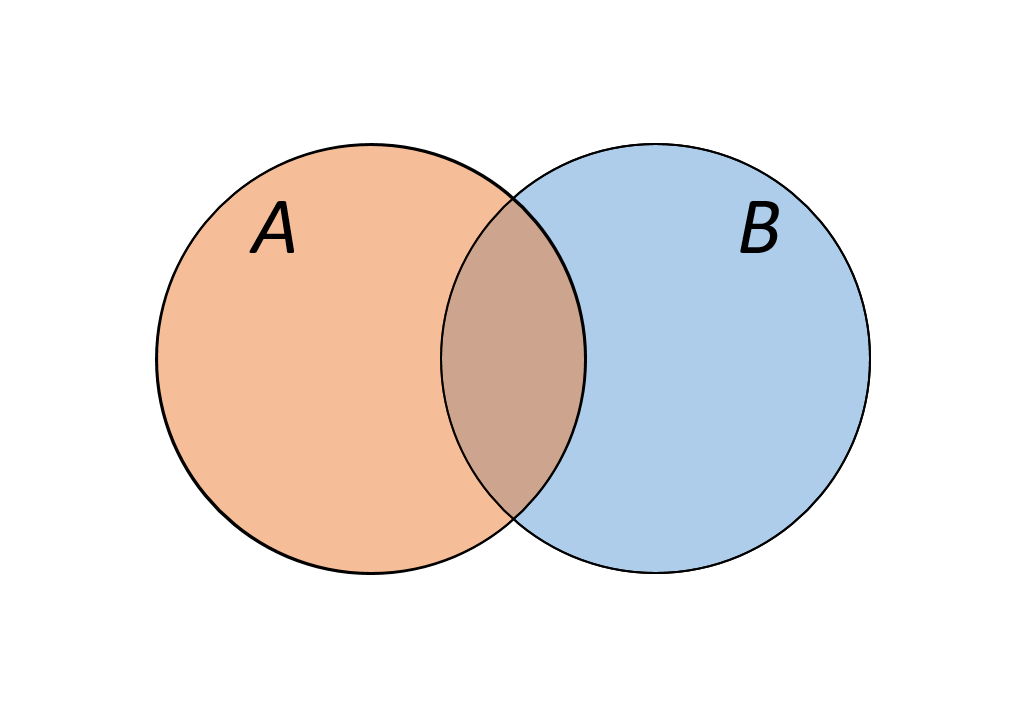
Пересекающимися понятиями, или находящимися в отношении перекрещивания, считаются те, объёмы которых совпадают частично. Пример: A — «математик», B — «репетитор»; A — «студент», B — «спортсмен». Часть объёма понятия «математик» входит в объём понятия «репетитор» и наоборот.
Понятия, состоящие в отношении подчинения, содержат одинаковые элементы, а объём подчинённого целиком входит в объём подчиняющего. Например, «млекопитающее» и «коза».
Несовместимыми называют понятия, не имеющие общих элементов:
Соподчинённые понятия имеют общие элементы и вместе входят в родовое понятие, но в их объёмах общие элементы отсутствуют. Например, А — «корова», B — «овца», C — «млекопитающее». Круги A и B необходимо поместить внутри круга, изображающего объём понятия C, но они не смогут пересекаться, так как не бывает млекопитающих, которые были бы и коровой, и овцой одновременно.
Противоположные понятия — это виды одного и того же рода, но одно из них имеет какой-то признак, а другое не обладает им и содержит признак, несовместимый с первым, направленный против него. Таковы A — «большой дом» и B — «маленький дом». Тут в отличие от отношения противоречия возможны предметы, которые не входят ни в A и ни в B. Если общее родовое C — дом, то в его круге будут изображения двух сегментов A и B, расположенных напротив друг друга, а оставшаяся часть должна соответствовать всем остальным домам (средним, меньше средних).
Противоречащими считается категория понятий, у одного из которых есть какой-то признак, а у другого он отрицается. Например, «чёрный» и «нечёрный», «злой» — «незлой». При этом весь массив родственных элементов делится на две части: одни имеют этот признак, а другие — нет.
Решение задач, примеры
Круги Эйлера и как решать сложные логические задачи, используя свойства диаграммы, можно показать на примерах.
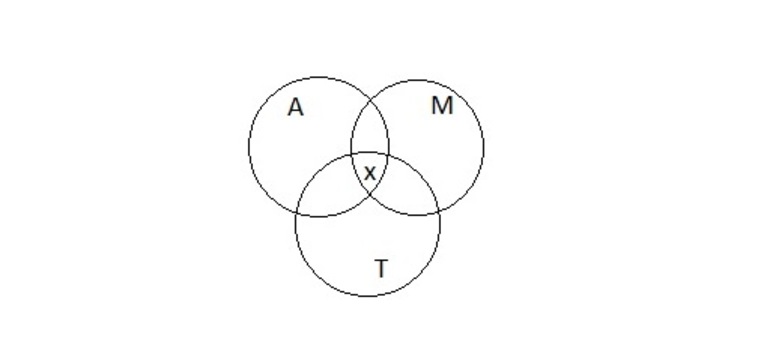
Задача 1. Пусть имеется следующее условие: 54 школьника шестых классов занимаются в авиамодельном, музыкальном и танцевальном кружках. Каждый посещает хотя бы один кружок. Музыкой занимаются 32 ученика, 22 — танцами, 34 — авиамоделированием. Участвуют в музыкальном и танцевальном кружках 11 школьников, в музыкальном и авиамоделировании — 21, в танцевальном и авиамоделировании — 12. Сколько учащихся посещают все три кружка?
Рисунок 2
Проект решения предполагает необходимость расписать всех 54 школьников в соответствии с условиями задачи. Известно, что в авиамодельном кружке 34 ученика. Если прибавить к этому число учеников, которые занимаются музыкой, их 32 человека, то получится A ⋃ M, где ⋃ обозначение объединения множеств, будет состоять из 34 + 32… учеников.
Но при взгляде на круги Эйлера (Рисунок 2) становится понятно, что те, кто занимается и музыкой, и авиамоделированием посчитаны дважды. Это область на диаграмме, которая принадлежит и кругу A, и кругу М, таких учеников 21. Значит, объединение множеств A ⋃ M будет 34 + 32 — 21…
Теперь нужно прибавить 22 школьника, занимающихся танцами. A ⋃ M ⋃ T равно 34 + 32 — 21 + 22… Тут опять некоторые ученики оказываются посчитаны дважды. Можно вычесть из общей суммы тех, кто занимается танцами и музыкой — 11 человек и 12 человек, участвующих в авиамодельном и танцевальном кружках одновременно. Функция принимает следующий вид: A ⋃ M ⋃ T будет 34 + 32 — 21 + 22 — 11 — 12…
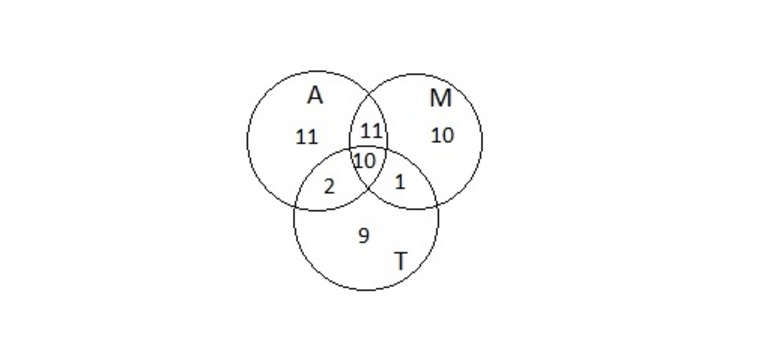
Но при этом школьники, которые посещают все три кружка, оказались отняты дважды. Их число обозначено x и его надо прибавить один раз к имеющейся формуле. Чтобы решить задачу, требуется определить x из полученного уравнения (Рисунок 3).
54 = 34 + 32 — 21 + 22 — 11 — 12 + х; откуда следует, что x = 10. Ответ: 10.
Рисунок 3
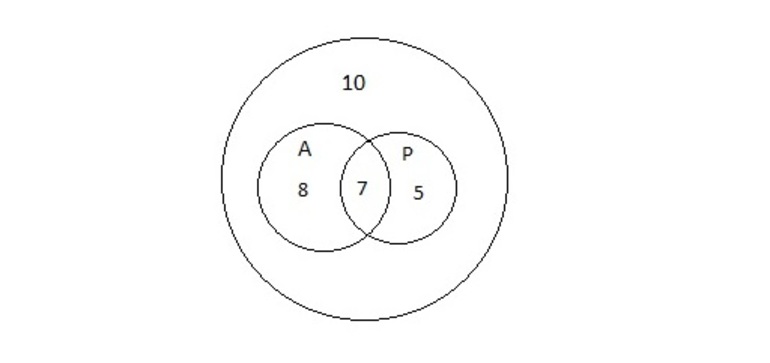
Задача 2. В школьную библиотеку пришло 30 учеников седьмого класса. Из них 15 человек взяли учебник по алгебре, 12 — по русскому языку, 10 человек не взяли ни одного учебника. Сколько учеников получили учебники по алгебре и русскому языку?
Множества на диаграммах представлены на рисунке 4. В большом круге 30 учеников, внутри двух малых 30 — 10 = 20 человек. По условию задачи 15 учеников получили учебник по алгебре, значит, 20 — 15 = 5 учеников получили только учебник по русскому языку. А в условии говорится, что 12 человек взяли учебник по русскому, то есть 12 — 5 = 7 школьников получили учебники и по алгебре, и по русскому. Ответ: 7.
Рисунок 4
Круги Эйлера часто применяются для решения самых разных задач. Они служат для развития способности к логическому мышлению у дошкольников. Большой раздел задач для школьников может решаться с помощью диаграмм. Многие учёные в своих исследованиях тоже обращаются к этому методу, который повышает наглядность решаемых проблем и помогает в их обдумывании. Использование простых фигур позволяет свести решение любой сложной задачи к символической логике и упростить ход рассуждений. Диаграммы могут применяться и в обычной жизни, например при поиске работы. Пересечение кругов «лучше всего получается», «больше всего нравится делать» и «чем можно заработать», возможно, даст нужный результат.
Как наглядно иллюстрируют соотношение между множествами
Различные объекты могут иметь отношения между собой.
» Останкинская телебашня находится в Москве;
» Один байт равен восьми битам;
» Лёша – брат Артёма и сын Ивана.
| Отношение – это взаимная связь между множествами.
Между городами А, Б, В, Г проложены автомобиль-ные дороги. Город А имеет сообщение с городами В, Г, город Б – с городом Г, город В – с городами А, Г.
Изобразим отношение между этими множествами наглядно:
Некоторые отношения изменяют порядок своего по-ложения в зависимости от условия. Такие отношения обозначают стрелкой.

Отношения между множествами
Отношения могут связывать множества объектов.
Для удобного представления таких отношений используют диаграммы Эйлера-Венна.
✒ Определение: Если множества А и В имеют общие элементы, то такие множества пересекаются.
Пусть А – множество интернет магазинов, В – множество всех магазинов одежды. В пересечение этих множеств попадают все интернет магазины одежды.
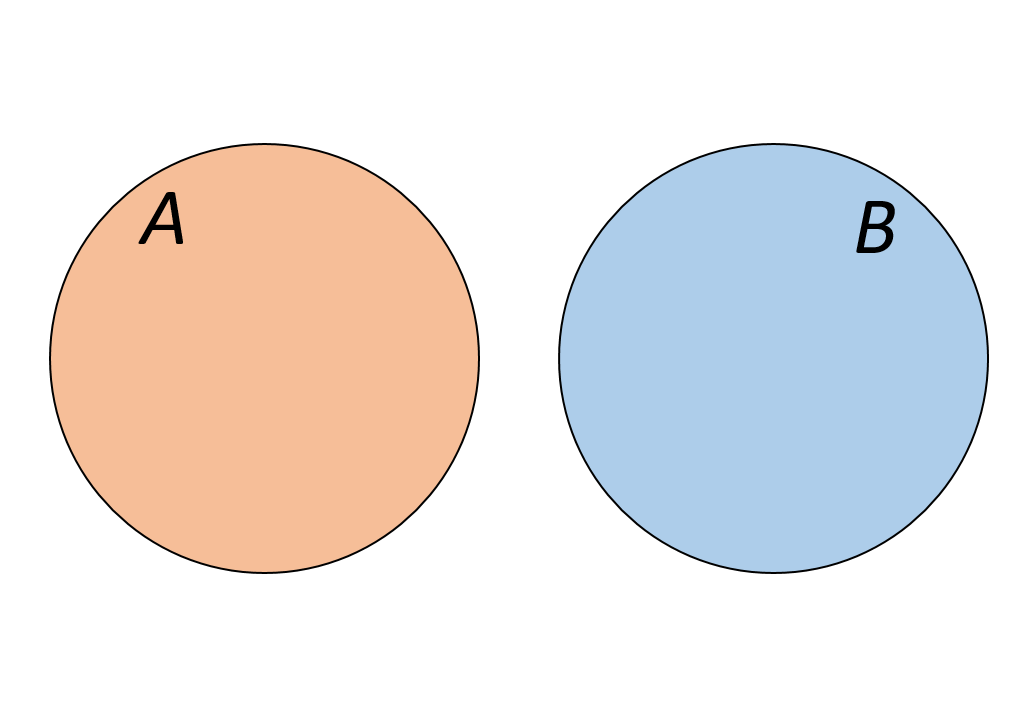
✒ Определение: Если множества не имеют общих элементов, то такие множества не пересекаются.
Пусть А – множество паровых двигателей, В – множество книг по биологии. Эти множества не имеют общих элементов.
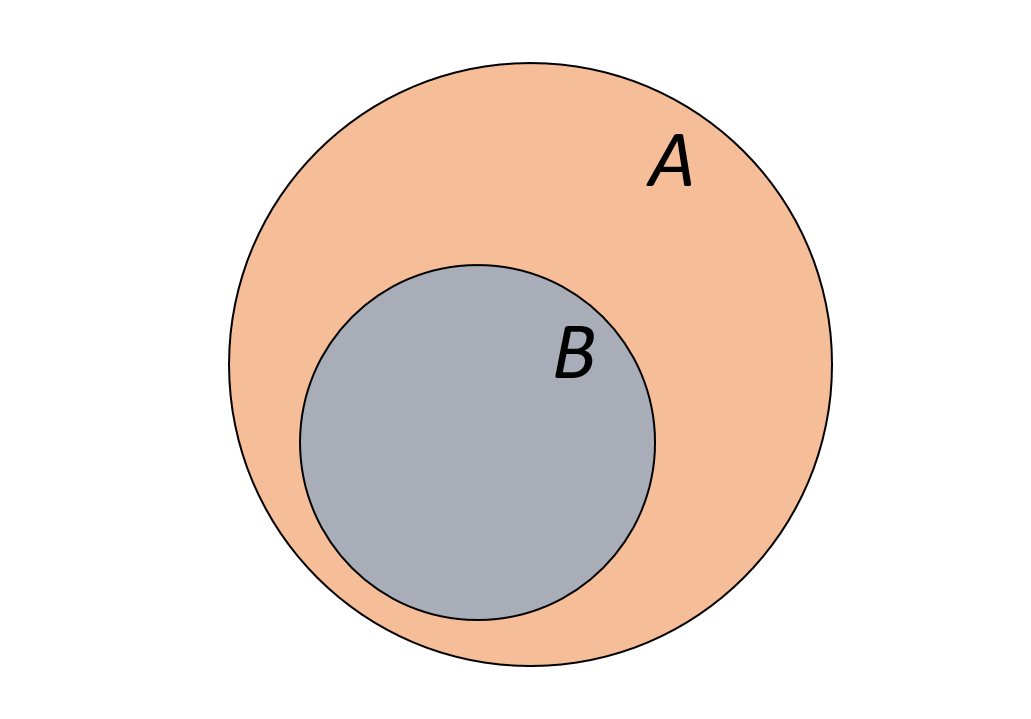
✒ Определение: Если каждый элемент В входит в множество А, то множество В – подмножество А.
Пусть А – множество литературных персонажей, В – множество героев романа Гарри Поттер. Множество героев романа является подмножеством множества литературных персонажей.
✒ Определение: Если каждый элемент множества В является элементом множества А и, на оборот, то множества А и В равны.
Пусть А – множество равносторонних прямоугольников, В – множество квадратов. Эти множества являются равными.
К уроку:
ПРЕЗЕНТАЦИЯ 
Задачи на диаграммы Эйлер-Венна.
Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной. Сколько шестиклассников являются читателями обеих библиотек?
А– посещающие школьную библиотеку (25);
B– посещающие районную библиотеку (20);
С– общее количество шестиклассников (35);
Обозначим за x – количество шестиклассников, посещающих обе библиотеке.
Ответ: 10 человек являются читателями обоих библиотеки.
В классе 25 учащихся. Из них 5 человек не умеют играть на в шашки, ни в шахматы. 18 учащихся умеют играть в шашки, 20 – в шахматы. Сколько учащихся класса играют и в шашки, и в шахматы?
В одном множестве 40 элементов, а в другом 30. Сколько элементов может быть в их:
Каждый ученик в классе изучает либо английский, либо французский язык, либо оба этих языка. Английский изучают 25 человек, французский – 27 человек, а тот и другой 18 человек. Сколько всего учеников в классе?
В детском саду 52 ребёнка. Каждый из них любит либо пирожное, либо мороженое, либо и то и другое. Половина детей любит пирожное, а 20 человек – пирожное и мороженое. Сколько детей любят мороженое?
В классе 35 учеников, каждый из них любит футбол, волейбол или баскетбол, а некоторые – два или даже три из этих видов спорта. 24 ученика любят футбол, 18 – волейбол, 12 баскетбол. При этом 10 учеников одновременно любят футбол и волейбол, 8 – футбол и баскетбол, а 5 – волейбол и баскетбол. Сколько учеников этого класса любят все три вида спорта.
Понятие множества и элемента множества. Способы задания множеств. Отношения между двумя множествами и изображение их при помощи кругов Эйлера
Множество – это основное неопределяемое понятие в математике.
– это группа объектов как единое целое.
Обозначение: A, B, C, D, E, …
Множество, не содержащее ни одного объекта, называется пустым и обозначается Ø.
N – мн. натуральных ч.
Q – мн. рациональных ч.
J – мн. иррациональных ч.
R – мн. действительных ч.
Объекты, из которых образовано множество, называются элементами множества.
Обозначение: a, b, c, d, e, …
Множества бывают конечные и бесконечные.
Способы задания множеств.
Множество задано, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит.
1.Перечисление всех его элементов
2.Использую характеристическое свойство.
Характеристическое свойство – такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
В – множество двузначных чисел.
Если множества заданы перечислением элементов, то достаточно перечислить их общие элементы.
Характеристическое свойство множества А ᴖ В составляется из характеристических свойств пересекаемых множеств с помощью союза «и».
Свойства (ко 2 и 3 вопросу):
Для любых двух множеств А и В справедливо равенство


В ᴖ А = < >=> А ᴖ В = В ᴖ А В ᴗ А = < >=>А ᴗ В = В ᴗ А
Для любых трех множеств А, В и С справедливо равенство
(А ᴗ В) ᴖ С = (А ᴖ С) ᴗ (В ᴖ С) (А ᴖ В) ᴗ С = (А ᴗ С) ᴖ (В ᴗ С)
Объединение множеств А и В называется множество, содержащие те и только те элементы, которые принадлежат множеству А или В.
Если множество, заданное перечислением его элементов, то чтобы получить объединение множеств надо перечислить элементы множества А и добавит из В недостающие элементы.
Если множества заданы указанием характеристического свойства, то используется союз «или».
3. Операции над множествами: разность множеств, дополнение к подмножеству, декартово произведение. Законы этих операций
Разностью множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А, но не принадлежат множеству В.
Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В, при условии, что В является подмножеством множества А.
Порядок выполнения действий с множествами:
3-объединение или разность
Доказательства законов с помощью кругов Эйлера.
Декартовым произведением множеств А и В называется множество всех пар 1-ая компонента которых принадлежит множеству А, а 2-ая – множеству В.
Способы задания декартово выражения
2.Указанием характеристического свойства
| А \ В | |
| (1;3) | (1;5) |
| (2;3) | (2;5) |
| (3;3) | (3;5) |
5) Множество А – интервал, множество В = R 6)A = R, B = R

2 0 (А×В)×С = А×(В×С) => ассоциативный закон не выполняется
3 0 Дистрибутивный закон декартово произведение относительно объединения

Дистрибутивный закон декартово произведение относительно вычитания
Дата добавления: 2015-04-18 ; просмотров: 47 ; Нарушение авторских прав