Как можно сравнить рациональные числа
Математика. 6 класс
Конспект урока
Сравнение рациональных чисел
Перечень рассматриваемых вопросов:
Две дроби с общим положительным знаменателем и равными числителями равны.
Из двух дробей с общим положительным знаменателем больше та, у которой числитель больше.
Чтобы сравнить две дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сравнить полученные дроби.
Теоретический материал для самостоятельного изучения
Рассмотрим на координатной оси
натуральные, целые и дробные числа.
Целые положительные: 1, 2, 3
Целые отрицательные: 1, 2, 3
Рациональные числа, как и целые, можно сравнивать с помощью числовой оси – чем правее расположено число, тем больше его координата.
Рассмотрим две отрицательные дроби
Сравнение рациональных чисел, представленных в виде дробей
с одинаковыми знаменателями.
Две дроби с общим положительным знаменателем и равными числителями равны.
Если у рациональных чисел, представленных в виде дробей одинаковый положительный знаменатель, и не равные числители, то переходим к сравнению числителей.
Правила сравнения рациональных чисел с нулём:
Сравнение рациональных чисел, представленных в виде дробей с разными знаменателями
Для начала ознакомимся с алгоритмом сравнения:
Получили две дроби с одинаковыми положительными знаменателями, теперь сравниваем их числители
Общий знаменатель равен 36.
Сравниваем модули числителей и пользуемся правилом: больше то число, числитель которого по модулю меньше.
Сравнение рациональных чисел
В статье рассмотрим основные моменты по теме сравнения рациональных чисел. Изучим схему сравнения чисел с различными знаками, сравнения нуля с любым рациональным числом, а также более детально разберем сравнение положительных рациональных чисел и сравнение отрицательных рациональных чисел. Всю теорию закрепим практическими примерами.
Сравнение рациональных чисел с разными знаками
Сравнение заданных чисел с разными знаками является простым и очевидным.
Любое положительное число больше любого отрицательного, а любое отрицательное число меньше любого положительного.
Сравнение рационального числа с нулем
Любое положительное число больше нуля; любое отрицательное число – меньше нуля.
Сравнение положительных рациональных чисел
Производя действие сравнения положительных рациональных чисел, нужно в первую очередь сравнить их целые части.
Большим является то число, у которого целая часть больше. Соответственно меньшим является число, целая часть которого меньше.
Решение
Решение
Ответ: заданные рациональные числа равны.
Мы рассмотрели практические примеры, когда целые части рациональных чисел не равны и подлежат сравнению. Если целые части заданных чисел равны, получить результат поможет сравнение дробных частей заданных чисел. Дробную часть всегда возможно записать в виде обыкновенной дроби вида m\n, конечной дроби или периодической десятичной дроби. Т.е. по сути сравнение дробных частей положительных чисел – это сравнение обыкновенных или десятичных дробей. Логично, что бОльшим из двух чисел с равными целыми частями является то, чья дробная часть больше.
Решение
Мы видим, что в результате применения обоих способов получен одинаковый результат сравнения заданных исходных рациональных чисел.
Сравнение отрицательных рациональных чисел
При сравнении двух отрицательных чисел бОльшим будет то число, модуль которого меньше и, соответственно, меньшим будет то число, модуль которого больше.
По сути указанное правило приводит сравнение двух отрицательных рациональных чисел к сравнению положительных, принцип которого мы разобрали выше.
Решение
Решение
Сравнение рациональных чисел, определения и примеры.
Чтобы выполнить сравнение рациональных чисел или сравнение дробей, необходимо знать простые правила. Как сравнивать рациональные числа? Рассмотрим подробнее.
Сравнение рациональных чисел с одинаковыми знаменателями.
Если у рациональных чисел одинаковый положительный знаменатель, то переходим к сравнению числителей.
Рассмотрим пример:
Сравните рациональные числа: а) \(\frac<3><20>\) и \(\frac<7><20>\) б) \(\frac<-5><13>\) и \(\frac<-7><13>\) в) \(\frac<4><7>\) и \(\frac<-5><7>\)
Решение:
а) Знаменатели одинаковые, переходим к сравнению числителей. У первого числителя число 3 у второго 7.
в) С дробями у которых разные знаки все просто, всегда больше положительная дробь
Сравнение рациональных чисел с нулем.
Правила сравнения рациональных чисел с нулем.
Рассмотрим пример:
Сравните с нулем рациональные числа: а) 0 и \(\frac<-1><33>\) б) \(\frac<3><4>\) и 0
Решение:
а) Дробь \(\frac<-1><33>\) отрицательна, поэтому нуль будет больше рационального числа.
б) Дробь положительна \(\frac<3><4>\), поэтому нуль будет меньше рационального числа.
Сравнение рациональных чисел с одинаковыми числителями и разными знаменателями.
Правило сравнение рациональных чисел с одинаковыми числителями:
Если у рациональных чисел одинаковые положительные числители и разные положительные знаменатели, та дробь больше у которой знаменатель меньше.
Разберем пример:
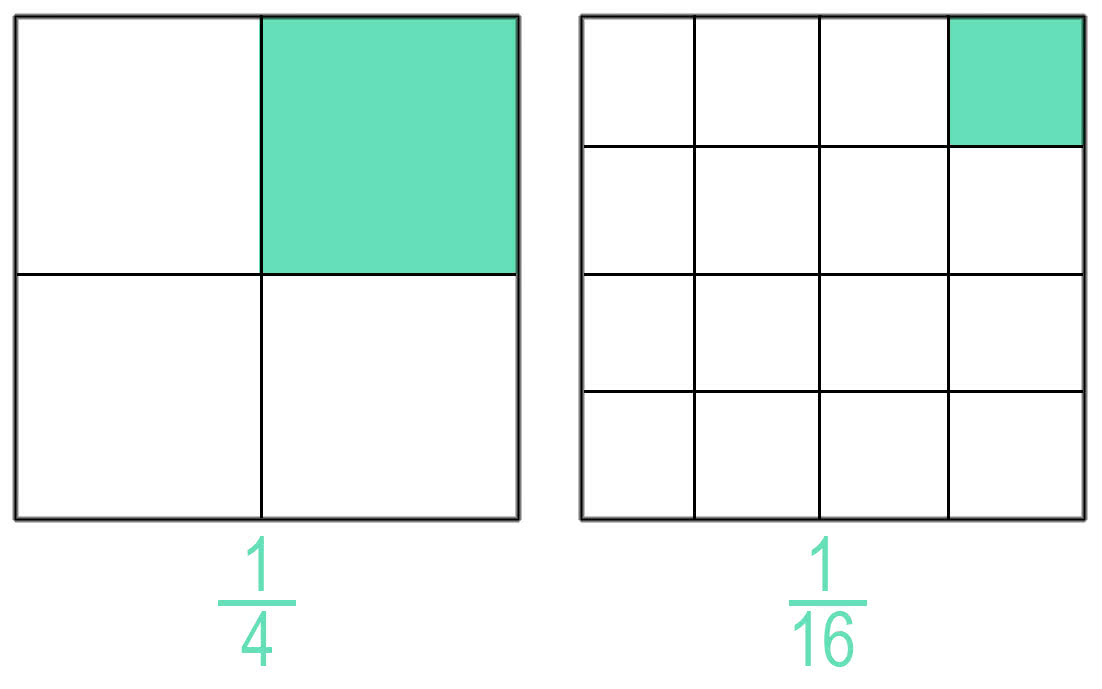
Сравните рациональные числа с одинаковыми числителями \(\frac<1><4>\) и \(\frac<1><16>\).
Решение:
Рассмотрим рисунок.
Видно, что взятая одна часть из четырех больше по размеру, чем взятая одна часть из 16. Поэтому, \(\frac<1> <4>> \frac<1><16>\)
Если у дробей одинаковые отрицательные числители и разные положительные знаменатели, то та дробь больше у которой знаменатель больше.
Рассмотрим тот же пример:
Сравните дроби с одинаковыми отрицательными числителями \(\frac<-1><4>\) и \(\frac<-1><16>\).
Решение:
Из выше решенной задачи на рисунке мы видели, что 1 часть из 16 по размеру меньше, а значит и числовое значение имеет меньше, чем 1 часть из 4. Но в отрицательных числах меньшее отрицательное число на числовой прямой лежит ближе, то есть левее к нулю чем большее число.
б) Найдем общий знаменатель дробей \(\frac<-5><6>\) и \(\frac<-2><3>\), чтобы сравнить их. Общий знаменатель равен 6.
в) Эти дроби \(\frac<1><2>\) и \(\frac<-7><10>\) можно не приводить к общему знаменателю, потому что у них разные знаки. Дробь с положительным знаком всегда больше дроби с отрицательным знаком.
\(\begin\frac<1> <2>> \frac<-7><10>\end\)
Одинаковые рациональные числа.
Рациональные числа равны тогда, когда при одинаковых знаменателях равны их числители. Например:
Математика. 6 класс
Конспект урока
Сравнение рациональных чисел
Перечень рассматриваемых вопросов:
Две дроби с общим положительным знаменателем и равными числителями равны.
Из двух дробей с общим положительным знаменателем больше та, у которой числитель больше.
Чтобы сравнить две дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сравнить полученные дроби.
Теоретический материал для самостоятельного изучения
Рассмотрим на координатной оси
натуральные, целые и дробные числа.
Целые положительные: 1, 2, 3
Целые отрицательные: 1, 2, 3
Рациональные числа, как и целые, можно сравнивать с помощью числовой оси – чем правее расположено число, тем больше его координата.
Рассмотрим две отрицательные дроби
Сравнение рациональных чисел, представленных в виде дробей
с одинаковыми знаменателями.
Две дроби с общим положительным знаменателем и равными числителями равны.
Если у рациональных чисел, представленных в виде дробей одинаковый положительный знаменатель, и не равные числители, то переходим к сравнению числителей.
Правила сравнения рациональных чисел с нулём:
Сравнение рациональных чисел, представленных в виде дробей с разными знаменателями
Для начала ознакомимся с алгоритмом сравнения:
Получили две дроби с одинаковыми положительными знаменателями, теперь сравниваем их числители
Общий знаменатель равен 36.
Сравниваем модули числителей и пользуемся правилом: больше то число, числитель которого по модулю меньше.
Сравнение рациональных чисел, правила, примеры.
В этой статье дается подробный обзор наиболее важных моментов, касающихся сравнения рациональных чисел. Если знаки сравниваемых чисел различны, то можно сразу сказать, какое число больше, а какое меньше, поэтому в самом начале мы разберем правило сравнения рациональных чисел с разными знаками. Дальше остановимся на сравнении нуля с другим рациональным числом. После этого подробно остановимся на сравнении положительных рациональных чисел. Наконец, перейдем к правилу сравнения отрицательных рациональных чисел. Теорию будем разбавлять решениями характерных примеров.
Навигация по странице.
Сравнение рациональных чисел с разными знаками
Проще всего выполнить сравнение двух рациональных чисел, имеющих разные знаки. При этом используется правило сравнения чисел с разными знаками: любое положительное число больше любого отрицательного, а любое отрицательное число меньше положительного.
Сравнение рационального числа с нулем
Очень просто проводится сравнение нуля с рациональным числом, отличным от нуля. При этом справедливо правило: любое положительное число больше нуля, а любое отрицательное число меньше нуля.
Сравнение положительных рациональных чисел
Сравнение положительных рациональных чисел следует начинать со сравнения их целых частей. При этом используется следующее правило: больше то число, целая часть которого больше, а меньше то число, целая часть которого меньше.
Какое из рациональных чисел 0,76 и 

исходные рациональные числа равны.
Проведите сравнение положительных рациональных чисел 3,7 и 
Покажем два способа.
Очевидно, оба способа нас привели к одинаковому результату сравнения исходных рациональных чисел.

Если равны и целые и дробные части сравниваемых положительных рациональных чисел, то эти числа равны.
Сравните числа 4,5 и 
Сравнение отрицательных рациональных чисел
Сравнение отрицательных рациональных чисел подчиняется правилу сравнения отрицательных чисел: из двух отрицательных чисел больше то, модуль которого меньше, и меньше то, модуль которого больше.
Это правило сводит сравнение отрицательных рациональных чисел к сравнению положительных рациональных чисел, разобранному в предыдущем пункте.
Сравните числа −15,2 и 

Выполните сравнение отрицательных рациональных чисел −1,11 и