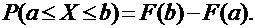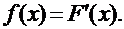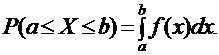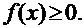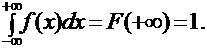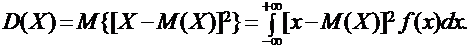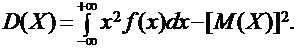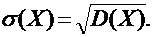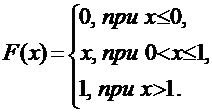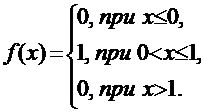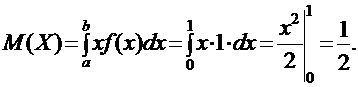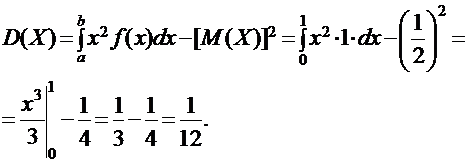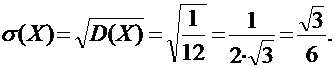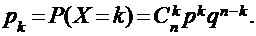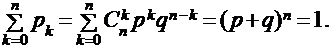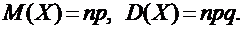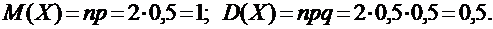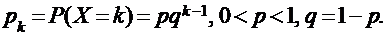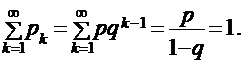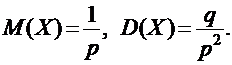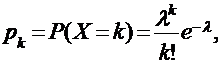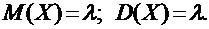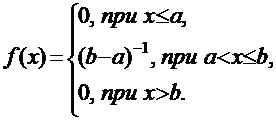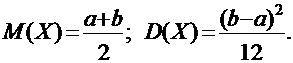дискретную случайную величину нельзя задать с помощью
Дискретная случайная величина
| Определение: |
| Случайная величина (англ. random variable) — отображение из множества элементарных исходов в множество вещественных чисел. [math] \xi\colon\Omega \to \mathbb |
Содержание
Дискретная случайная величина [ править ]
| Определение: |
| Дискретной случайной величиной (англ. discrete random variable) называется случайная величина, множество значений которой не более чем счётно, причём принятие ею каждого из значений есть случайное событие с определённой вероятностью. |
Примеры [ править ]
Проще говоря, дискретные случайные величины — это величины, количество значений которых можно пересчитать. Например:
Существуют также непрерывные случайные величины. Например, координаты точки попадания при выстреле.
Функция распределения [ править ]
Если случайная величина [math]\xi[/math] дискретна, то есть её распределение однозначно задаётся функцией [math]\mathbb
(\xi = x_i) = p_i,\; i=1,2,\ldots[/math]
Функция распределения [math]F(x)[/math] этой случайной величины кусочно-постоянна и может быть записана как [math]F(x) = \sum\limits_ Свойства функции распределения дискретной случайной величины: В отличие от дискретной случайной величины, непрерывная случайная величина может принять любое действительное значение из некоторого промежутка ненулевой длины, что делает невозможным её представление в виде таблицы или перечисления состояний. Поэтому ее часто явно задают через функцию распределения, например [math] F(x) = \begin Свойства функции плотности вероятности: Для примера выше [math] f(x)=F'(x) = \begin Для дискретной случайной величины не существует функции плотности распределения вероятностей, так как такая случайная величина не является абсолютно непрерывной функцией. Непрерывной называется случайная величина Х, если ее функция распределения непрерывна на множестве ее возможных значений. Распределение непрерывной случайной величины однозначно определяется ее функцией распределения F(x), т.к.: Из этой формулы следует, что вероятность каждого конкретного значения непрерывной случайной величины равна нулю. Все свойства, сформулированные нами в предыдущем подразделе для функций распределения дискретных случайных величин, выполняются и для функций распределения непрерывных случайных величин. Непрерывную случайную величину можно также задать, используя функцию, которую принято называть плотностью распределения вероятностей, или просто плотностью распределения. Плотностью распределения непрерывной случайной величины Х называется производная от функции распределения этой случайной величины, т.е.: Плотность распределения однозначно определяет распределение непрерывной случайной величины, поскольку: И, кроме того, по определению: Перечислим основные свойства плотности распределения: 1. Плотность распределения является неотрицательной функцией, т.е. 2. Математическое ожидание М(Х) непрерывной случайной величины Х определяется формулой: Дисперсия D(X) непрерывной случайной величины Х определяется формулой: На практике для вычисления дисперсии непрерывных случайных величин используется другая формула: Среднее квадратическое отклонение непрерывной случайной величины Х определяется, так же как и для дискретных случайных величин, формулой: Все свойства математического ожидания и дисперсии, сформулированные нами для дискретных случайных величин, без каких либо изменений остаются справедливыми и для непрерывных случайных величин. ПРИМЕР:Найти математическое ожидание, дисперсию и среднее квадратическое отклонение непрерывной случайной величины Х, если она задана функцией распределения вида: Для данной случайной величины функция распределения является кусочно-непрерывной, поэтому для плотности распределения можно найти: Искомое математическое ожидание случайной величины Х найдем по формуле: Искомую дисперсию найдем по формуле: Наконец, среднее квадратическое отклонение найдем по формуле: Рекомендуемая литература по теме 1.3:[1 ÷ 4]. ВОПРОСЫ для самопроверки знаний по теме 1.3: 1. Вероятность какого события является значением функции распределения случайной величины? 2. Каким является множество значений дискретной случайной величины? 3. Почему нельзя дискретную случайную величину задавать с помощью плотности распределения? 4. Какая числовая характеристика имеет смысл среднего значения случайной величины? 5. Какая числовая характеристика оценивает степень рассеивания случайной величины? 6. Чем определяется величина скачка функции распределения дискретной случайной величины в точке разрыва? 7. Чему равны наименьшее и наибольшее значения функции распределения? Тема 1.4. Законы распределения случайных величин 1.4.1. Биномиальное распределение Пусть проводятся n испытаний по схеме Бернулли с вероятностью успеха р и вероятностью неуспеха q и p + q = 1. В этом случае дискретная случайная величина Х – число успехов может принимать любое из своих возможных значений Такое распределение называется биномиальным с параметрами р и q. Заметим, что сумма этих вероятностей будет равна: Математическое ожидание и дисперсия случайной величины Х, имеющей биномиальное распределение будет определяться формулами: ПРИМЕР: Случайная величина Х – число выпадений герба при двух бросаниях монеты имеет биномиальное распределение с возможными значениями 1.4.2. Геометрическое распределение Дискретная случайная величина Х имеет геометрическое распределение, если она принимает значения k = 1, 2, 3, … (счетное множество значений) с вероятностями, определяемыми формулой: Определение является корректным, поскольку сумма вероятностей возможных значений будет равна: Случайная величина Х, имеющая геометрическое распределение, представляет собой число испытаний по схеме Бернулли до первого успеха. Математическое ожидание и дисперсия такой величины определяются формулами: ПРИМЕР: В большой партии изделий вероятность брака равна р. Контроль качества проводится до первого появления бракованного изделия. В результате серии проверок обнаружилось, что бракованное изделие впервые появлялось в среднем при десятом испытании. Оценить вероятность р. Пусть Х – число испытаний до первого появления бракованного изделия. Эта случайная величина имеет геометрическое распределение. Согласно условию ее среднее значение равно: Распределение Пуассона Дискретная случайная величина Х имеет распределение Пуассона, если она принимает целые значения k = 0, 1, 2, … с вероятностями, определяемыми по формуле Пуассона: где l > 0 – параметр распределения. При этом: Математическое ожидание и дисперсия величины Х в этом случае: Равномерное распределение Непрерывная случайная величина Х распределена равномерно на отрезке [a, b], если ее плотность распределения имеет вид: График функции плотности распределения в этом случае приведен на рис. 1.2. Математическое ожидание и дисперсия равномерно распределенной случайной величины определяются формулами: ПРИМЕР: Интервал движения автобуса равен 15 минутам. Какова вероятность того, что пассажир на остановке будет ждать автобус более 5 минут? Пусть случайная величина Х – время ожидания автобуса. Она распределена равномерно на отрезке [0, 15], а ее плотность распределения имеет вид: Тогда искомая вероятность будет равна: Дата добавления: 2018-06-01 ; просмотров: 423 ; Мы поможем в написании вашей работы! Рис. 1.1. Плотность треугольного распределения Рис.1.2. Плотность показательного распределения Рис.1.3. Плотность нормального распределения Проверка качества последовательностей псевдослучайных чисел Дискретная случайная величина — это такая случайная величина, значения которой могут быть не более чем счетными, то есть либо конечными, либо счетными. Под счетностью имеется ввиду, что значения случайной величины можно занумеровать. Пример 1. Приведем примеры дискретных случайных величин: в) число прибывших кораблей на борт (счетное множество значений). г) число вызовов, поступающих на АТС (счетное множество значений). $\begin $\begin Возможные значения случайных величин с равными математическими ожиданиями могут по-разному рассеиваться вокруг своих средних значений. Например, в двух студенческих группах средний балл за экзамен по теории вероятностей оказался равным 4, но в одной группе все оказались хорошистами, а в другой группе — только троечники и отличники. Поэтому возникает необходимость в такой числовой характеристике случайной величины, которая бы показывала разброс значений случайной величины вокруг своего математического ожидания. Такой характеристикой является дисперсия. Способ представления дискретной случайной величины в виде ряда распределения не является единственным, а главное он не является универсальным, поскольку непрерывную случайную величину нельзя задать с помощью ряда распределения. Существует еще один способ представления случайной величины — функция распределения.Примеры [ править ]
Функция плотности распределения вероятностей [ править ]
Непрерывные случайные величины
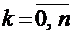
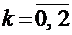
Дискретную случайную величину нельзя задать с помощью
Показательное (экспоненциальное) распределение. Случайная величина X имеет показательное (экспоненциальное) распределе¬ние с параметром λ(λ> 0), если ее плотность вероятности вычисляет¬ся по формуле
Нормальное распределение. Случайная величина X имеет нормальное распределение с параметрами m и σ2, если ее плотность вероятности вычисляется по формуле
Нормально распределенная случайная величина с большой вероятностью при¬нимает значения, близкие к своему математическому ожиданию.
На ЭВМ невозможно получить идеальную последовательность случайных чисел хотя бы потому, что на ней можно оперировать только с конечным множеством чисел. Кроме того, для получения значений х случайной величины ζ используются формулы (алгорит¬мы). Поэтому такие последовательности, являющиеся по своей сути детерминированными, называются псевдослучайными.
Полу¬ченные с помощью генератора псевдослучайные последовательности чисел должны состоять из квазиравномерно распределенных чисел, содержать статистически независимые числа, быть воспроизводимыми, иметь неповторяющиеся числа, получать¬ся с минимальными затратами машинного времени, занимать минимальный объем машинной памяти.
Моделирование случайных величин с помощью компьютера основано на преобразовании случайных чисел, имеющих равномерное распределение на интервале [0, 1] в случайные величины, имеющие другие распределения.
Получение случайных чисел, имеющих равномерное распределение на интервале [0, 1] возможно различными способами.
Мультипликативный способ заключается в следующем: если ri = 0,0040353607, то ri+1 = <40353607•ri >mod 1, где mod 1 означает операцию извлечения из результата только дробной части после десятичной точки. Литературные источники говорят, что числа ri, начинают повторяться после цикла из 50 миллионов чисел, так что r50000001= ri. Последовательность ri получается квазиравномерно распределенной на интервале (0, 1). Однако, наиболее часто используются стандартную функцию, имеющуюся в языках программирования. Будем называть эту функцию random().Дискретные случайные величины
1. Закон распределения вероятностей дискретной случайной величины.
\hline
X_i & x_1 & x_2 & \dots & x_n \\
\hline
p_i & p_1 & p_2 & \dots & p_n \\
\hline
\end
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end2. Математическое ожидание дискретной случайной величины.
3. Дисперсия дискретной случайной величины.
4. Функция распределения дискретной случайной величины.