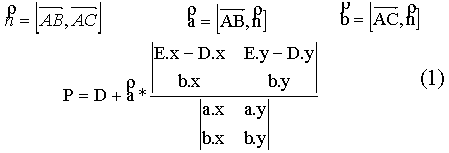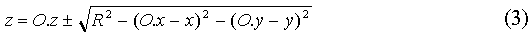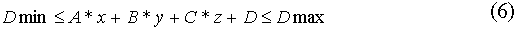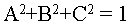Как называется треугольник в пространстве

Сферические треугольники — использование в трехмерной графике

За последние несколько лет трехмерная компьютерная графика сделала гигантский шаг вперед. Качество и реалистичность, казавшиеся невозможными раньше, сейчас реализуются графическими ускорителями, доступными самому широкому кругу пользователей. Однако, принципы создания и визуализации трехмерных сцен и объектов практически не изменились. Базовым графическим примитивом по прежнему является треугольник. Каждый объект сцены разбивается на треугольники и в таком виде хранится и выводится на экран. Недостатки такого подхода очевидны: сложные объекты получаются либо слишком угловатыми, либо содержат огромное количество мелких треугольников, что приводит к существенному падению производительности. Таким образом, разработчикам и дизайнерам компьютерных игр приходится постоянно делать выбор между скоростью и качеством. Надо сказать, что разработано множество способов, позволяющих улучшить качество при минимальных вычислительных затратах, но даже они не способны скрыть угловатую сущность треугольника.

Почему бы тогда не отказаться от плоского треугольника в пользу более криволинейных геометрических примитивов? Дело в том, что использование кривых поверхностей в общем случае приводит к необходимости производить большое количество операций с вещественными числами. Такие примитивы используются в профессиональной трехмерной графике, но в системах визуализации в реальном времени (компьютерных играх) они не применимы в силу своей вычислительной сложности. Хотя и в этом направление ведутся работы, например в этой статье предлагается в качестве примитивов использовать квадрики с функциями возмущения, что позволяет создавать сложные формы объектов, используя минимум примитивов. Тем не менее, мне кажется, что в ближайшее время не стоит ожидать появления широко доступных графических ускорителей, способных обеспечить достаточно высокую скорость отрисовки подобных поверхностей.

В качестве альтернативы плоским треугольникам и сложным криволинейным функциям, я предлагаю рассмотреть такие графические примитивы, как сферические треугольники.

Сферический треугольник — это три точки на сфере, соединенные дугами большого круга. Наиболее интересны эйлеровы сферические треугольники — это те, что полностью лежат в одном полушарии. С одной стороны, они уже не являются плоскими объектами, а с другой — могут быть легко заданы тремя вершинами и радиусом окружности, на которой они лежат (радиусом кривизны). На самом деле это задание не однозначно — треугольник может быть как выпуклым, так и вогнутым. Будем считать, что треугольник с положительным радиусом кривизны — выпуклый, с отрицательным — вогнутый.

Использование сферических треугольников вместе с плоскими треугольниками дает множество преимуществ:

Иллюстрации к этой статье были отрендерены в специально написанной демонстрационной программе. Эта программа читает информацию о сцене из текстового файла, указанного в качестве параметра. Таким образом, можно создавать свои собственные сцены. Только нужно учесть, что эта программа не умеет выводить плоские треугольники — только сферические. Хотя сферический треугольник с большим радиусом кривизны вполне может сойти за плоский.

Проекция сферического треугольника на картинную плоскость с наложением текстуры

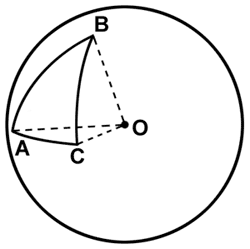
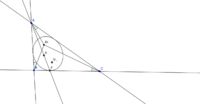
Прежде всего, нужно найти центр сферы, на которой лежит этот треугольник.

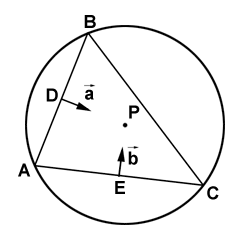
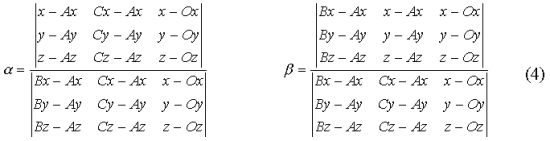
Для этого, рассмотрим плоскость, в которой лежат все три вершины A, B, C треугольника. Пересечение сферы и плоскости дает окружность, которая является описанной вокруг треугольника окружностью. Ее центр P лежит в точке пересечения срединных перпендикуляров и может быть найден по следующей формуле:

Если детерминант в знаменателе равен нулю, его можно заменить на такой же, но с другой парой координат — (y, z) или (x, z). Один из них будет неравен нулю хотя бы потому, что векторное произведение a и b ненулевой вектор.

Вектор с началом в центре сферы O и концом в центре окружности P коллинеарен вектору нормали n. Таким образом, мы получаем прямоугольный треугольник APO, гипотенуза и один катет которого известны. Это позволяет найти точку O по следующей формуле:

От знака перед корнем в этой формуле зависит будет треугольник выпуклым или вогнутым. Мы договорились, что выпуклость/вогнутость будет задаваться знаком радиуса, именно в этом месте он и играет роль.

Центр сферы достаточно найти только один раз — в дальнейшем, нужно лишь применять к нему те же трансформации, что и к вершинам.

Предположим, что геометрию мы рассчитали и теперь нужно вывести сферический треугольник на картинную плоскость. Прежде всего, полезно определить видим ли он вообще. Плоский треугольник считается видимым, если его нормаль направлена в сторону картинной плоскости. Со сферическими треугольниками все немного сложнее. Сферический треугольник видим, если хотя бы один из векторов OA, OB, OC направлен в сторону картинной плоскости.

После проверки на видимость, сферический треугольник нужно спроецировать на картинную плоскость. Будем считать, что она совпадает с плоскостью z = 0, а проектирующие прямые параллельны оси O_z.

Процесс проецирования организуем следующим образом — просканируем все пиксели окна вывода картинной плоскости и для каждого определим цвет, если он лежит внутри сферического треугольника. На самом деле, существуют методы, позволяющие обойтись без сканирования всего окна вывода, ограничиться только пикселями, лежащими внутри границ треугольника. Проблема тут в том, что границы — это эллиптические кривые. Упомянутая выше демонстрационная программа реализует один из этих методов, причем с довольно высокой скоростью. Но этот способ довольно сложен и относится скорее к методам программной оптимизации, поэтому я оставлю его за рамками этой статьи. Будем считать, что сканируется все окно вывода.

Получив координаты (x, y) пикселя, нужно найти z координату точки X на сфере, проецирующейся в этот пиксель. Это можно сделать пользуясь следующей формулой:

Если выражение под корнем меньше нуля, то в данный пиксель не проектируется ни одна точка сферы. Если равно нулю, то существует только одна такая точка. Если больше нуля, то таких точки две — на внешней поверхности сферы и на внутренней. Какую из них выбрать — это опять вопрос выпуклости/вогнутости, а как следствие, знака радиуса.

Знание z-координаты дает множество возможностей, например, можно воспользоваться z-буфером для проверки видимости.

Чтобы избавиться от этих эффектов, я предлагаю разлагать вектор AX по базису векторов AB, AC и OX. Использование вектора OX привносит нелинейные искажения, «растягивающие» текстуру на весь сферический треугольник. Разложение осуществляется следующими формулами (нам нужны только первые две координаты, поэтому третью формулу я опустил):

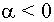
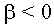
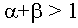
Если или или , то точка находится за пределами данного сферического треугольника и может быть исключена из дальнейшего рассмотрения.

Текстурные координаты (X_u, X_v) находятся по следующим формулам:

Зная текстурные координаты и текстуру, найти цвет пикселя уже легко.

Хотя формулы выглядят довольно громоздко, их программная реализация работает достаточно быстро.

Некоторые проблемы и пути их решения

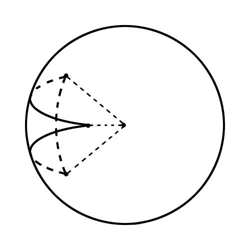
При моделировании «летающей тарелки» у меня возникла следующая проблема:

Оказалось, что как бы я ни старался, уголки треугольников торчат в месте стыка. Дело в том, что, как я уже писал, сферический треугольник образуется тремя дугами больших кругов. А это значит, что только в районе экватора нижние грани треугольников лежат в одной плоскости. Но тогда «тарелка» вырождается в сферу. Можно разбить каждую половинку на множество сферических треугольников, но это противоречит самой идее использования этих примитивов.

Чтобы избавиться от этих артефактов, я предлагаю следующий метод. Сферическому треугольнику дополнительно назначается плоскость (A, B, C, D), а также два числа D_min и D_max — начальное и конечное расстояние от плоскости, диапазон, по которому отсекается треугольник. То есть, в процесс проектирования добавляется проверка:

Подразумевается, что

Эта проверка позволяет значительно расширить возможности сферических треугольников. Например, используя этот метод, можно получить такой объект:

При этом, падения скорости не наблюдается, временами даже наоборот.

Заключение

Использование сферических треугольников в задачах компьютерной графики имеет как свои плюсы, так и минусы. Очевидно, что эти примитивы не смогут полностью удовлетворить разработчиков трехмерных приложений или вытеснить плоские треугольники. Я ни в коем случае не позиционирую описанные методы как альтернативу существующим системам. Но использование сферических треугольников совместно с другими технологиями способно дать еще одну степень свободы создателям трехмерных миров. Этим, наверное, стоит воспользоваться.

Источник

Треугольник

Треуго́льник (в евклидовом пространстве) — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла. Если три точки лежат на одной прямой, то «треугольник» с вершинами в трёх данных точках называется вырожденным. Все остальные треугольники невырожденные.

В неевклидовых пространствах в качестве сторон треугольника выступают геодезические линии, которые, как правило, являются криволинейными. Поэтому такие треугольники называют криволинейными.

Содержание

Элементы треугольника

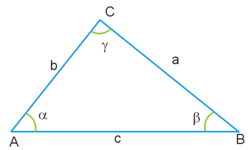
Треугольник с вершинами A, B и C обозначается как (см. рис.). Треугольник имеет три стороны:

Длины сторон треугольника обозначаются строчными латинскими буквами (a, b, c):

Треугольник имеет следующие углы:

Величины углов при соответствующих вершинах традиционно обозначаются греческими буквами (α, β, γ).

Признаки равенства треугольников

Треугольник на евклидовой плоскости однозначно (с точностью до конгруэнтности) можно определить по следующим тройкам основных элементов:

Признаки равенства прямоугольных треугольников:

В сферической геометрии и в геометрии Лобачевского существует признак равенства треугольников по трём углам.

Типы треугольников

Типы треугольников
Файл:Triangle-acute.svg Остроугольный	Файл:Triangle-obtuse.svg Тупоугольный	Прямоугольный
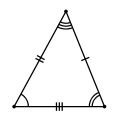Разносторонний	Файл:Triangle-isosceles.svg Равнобедренный	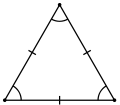Равносторонний

По величине углов

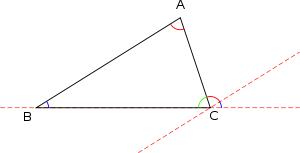
Поскольку в евклидовой геометрии сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:

В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а на сфере — всегда больше. Разность суммы углов треугольника и 180° называется дефектом. Дефект пропорционален площади треугольника, таким образом, у бесконечно малых треугольников на сфере или плоскости Лобачевского сумма углов будет мало отличаться от 180°.

По числу равных сторон

Определения, связанные с треугольником

Все факты, изложенные в этом разделе, из евклидовой геометрии.

Лучи, отрезки и точки

В равнобедренном треугольнике медиана, высота и биссектриса, проведённые к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный. Если треугольник разносторонний, то для любой его вершины биссектриса, проведённая из неё, лежит между медианой и высотой, проведёнными из той же вершины.

Чевианы, лежащие на прямых, симметричных медианам относительно биссектрис, называются симедианами. Они проходят через одну точку — точку Лемуана.

Некоторые точки в треугольнике — «парные». Например, существует две точки, из которых все стороны видны либо под углом в 60°, либо под углом в 120°. Они называются точками Торричелли. Также существует две точки, проекции которых на стороны лежат в вершинах правильного треугольника. Это — точки Аполлония. Точки и такие, что и называются точками Брокара.

Прямые

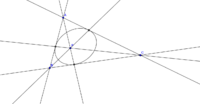
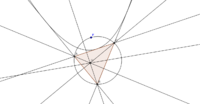
В любом треугольнике центр тяжести, ортоцентр и центр описанной окружности лежат на одной прямой, называемой прямой Эйлера.

Прямая, проходящая через центр описанной окружности и точку Лемуана, называется осью Брокара. На ней лежат точки Аполлония. Также на одной прямой лежат точки Торричелли и точка Лемуана. Основания внешних биссектрис углов треугольника лежат на одной прямой, называемой осью внешних биссектрис. На одной прямой лежат также точки пересечения прямых, содержащих стороны ортотреугольника, с прямыми, содержащими стороны треугольника. Эта прямая называется ортоцентрической осью, она перпендикулярна прямой Эйлера.

Если на описанной окружности треугольника взять точку, то её проекции на стороны треугольника будут лежать на одной прямой, называемой прямой Симсона данной точки. Прямые Симсона диаметрально противоположных точек перпендикулярны.

Треугольники

Окружности

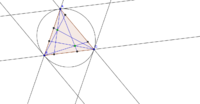
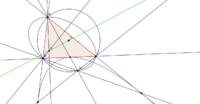
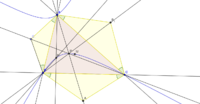
Середины трёх сторон треугольника, основания трёх его высот и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек или окружностью Эйлера. Центр окружности девяти точек лежит на прямой Эйлера. Окружность девяти точек касается вписанной окружности и трёх вневписанных. Точка касания вписанной окружности и окружности девяти точек называется точкой Фейербаха. Если от каждой вершины отложить наружу треугольника на прямых, содержащих стороны, ортезки, равные по длине противоположным сторонам, то получившиеся шесть точек лежат на одной окружности — окружности Конвея. В любой треугольник можно вписать три окружности таким образом, что каждая из них касается двух сторон треугольника и двух других окружностей. Такие окружности называются окружностями Мальфатти. Центры описанных окружностей шести треугольников, на которые треугольник разбивается медианами, лежат на одной окружности, которая называется окружностью Ламуна.

В треугольнике есть три окружности, которые касаются двух сторон треугольника и описанной окружности. Такие окружности называют полувписанными или окружностями Веррьера. Отрезки, соединяющие точки касания окружностей Веррьера с описанной окружностью, пересекаются в одной точке, называемой точкой Веррьера. Она служит центром гомотетии, которая переводит описанную окружность во вписанную. Точки касания окружностей Веррьера со сторонами лежат на прямой, которая проходит через центр вписанной окружности.

Отрезки, соединяющие точки касания вписанной окружности с вершинами, пересекаются в одной точке, называемой точкой Жергонна, а отрезки, соединяющие вершины с точками касания вневписанных окружностей — в точке Нагеля.

Эллипсы, параболы и гиперболы

В треугольник можно вписать бесконечно много коник (эллипсов, парабол или гипербол). Если в треугольник вписать произвольную конику и соединить точки касания с противоположными вершинами, то получившиеся прямые пересекутся в одной точке, называемой перспектором коники. Для любой точки плоскости, не лежащей на стороне или на её продолжении существует вписанная коника с перспектором в этой точке. [1]

В треугольник можно вписать эллипс, который касается сторон в серединах. Такой эллипс называется вписанным эллипсом Штейнера (его перспектором будет центроид треугольника). [2] Описанный эллипс, который касается прямых, проходящих через вершины параллельно сторонам, называется описанным эллипсом Штейнера. Если аффинным преобразованием («перекосом») перевести треугольник в правильный, то его вписанный и описанный эллипс Штейнера перейдут во вписанную и описанную окружности. Чевианы, проведённые через фокусы описанного эллипса Штейнера (точки Скутина), равны (теорема Скутина). Изо всех описанных эллипсов описанный эллипс Штейнера имеет наименьшую площадь, а изо всех вписанных наибольшую площадь имеет вписанный эллипс Штейнера. [3]

Эллипс с фокусами в точках Брокара называется эллипсом Брокара. Его перспектором служит точка Лемуана. [4]

Перспекторы вписанных парабол лежат на описанном эллипсе Штейнера. [5] Фокус вписанной параболы лежит на описанной окружности, а директриса проходит через ортоцентр. [6] Парабола, вписанная в треугольник, имеющая директрисой прямую Эйлера, называется параболой Киперта. Её перспектор — четвёртая точка пересечения описанной окружности и описанного эллипса Штейнера, называемая точкой Штейнера.

Если описанная гипербола проходит через точку пересечения высот, то она равносторонняя (то есть её асимптоты перпендикулярны). [7] Точка пересечения асимптот равносторонней гиперболы лежит на окружности девяти точек. [7]

Преобразования

Если прямые, проходящие через вершины и некоторую точку, не лежащую на сторонах и их продолжениях, отразить относительно соответствующих биссектрис, то их образы также пересекутся в одной точке, которая называется изогонально сопряжённой исходной (если точка лежала на описанной окружности, то получившиеся прямые будут параллельны). Изогонально сопряжёнными являются многие пары замечательных точек: центр описанной окружности и ортоцентр, центроид и точка Лемуана, точки Брокара. Точки Аполлония изогонально сопряжены точкам Торричелли, а центр вписанной окружности изогонально сопряжён сам себе. Под действием изогонального сопряжения прямые переходят в описанные коники, а описанные коники — в прямые. Так, изогонально сопряжены гипербола Киперта и ось Брокара, гипербола Енжабека и прямая Эйлера, гипербола Фейербаха и линия центров вписанной о описанной окружностей. Описанные окружности подерных треугольников изогонально сопряжённых точек совпадают. Фокусы вписанных эллипсов изогонально сопряжены.

Если вместо симметричной чевианы брать чевиану, основание которой удалено от середины стороны так же, как и основание исходной, то такие чевианы также пересекутся в одной точке. Получившееся преобразование называется изотомическим сопряжением. Оно также переводит прямые в описанные коники. Изотомически сопряжены точки Жергонна и Нагеля. При аффинных преобразованиях изотомически сопряжённые точки переходят в изотомически сопряжённые. При изотомическом сопряжении в бесконечно удалённую прямую перейдёт описанный эллипс Штейнера.

Если в сегменты, отсекаемые сторонами треугольника от описанного круга, вписать окружности, касающиеся сторон в основаниях чевиан, проведённых через некоторую точку, а затем соединить точки касания этих окружностей с описанной окружностью с противоположными вершинами, то такие прямые пересекутся в одной точке. Преобразование плоскости, сопоставляющее исходной точке получившуюся, называется изоциркулярным преобразованием. Композиция изогонального и изотомического сопряжений является композицией изоциркулярного преобразования с самим собой. Эта композиция — проективное преобразование, которое стороны треугольника оставляет на месте, а ось внешних биссектрис переводит в бесконечно удалённую прямую.

Если продолжить стороны чевианного треугольника некоторой точки и взять их точки пересечения с соответствующими сторонами, то полученные точки пересечения будут лежать на одной прямой, называемой трилинейной полярой исходной точки. Ортоцентрическая ось — трилинейная поляра ортоцентра; трилинейной полярой центра вписанной окружности служит ось внешних биссектрис. Трилинейные поляры точек, лежищих на описанной конике, пересекаются в одной точке (для описанной окружности это точка Лемуана, для описанного эллипса Штейнера — центроид). Композиция изогонального (или изотомического) сопряжения и трилинейной поляры является преобразованием двойственности (если точка, изогонально (изотомически) сопряжённая точке , лежит на трилинейной поляре точки , то трилинейная поляра точки, изогонально (изотомически) сопряжённой точке лежит на трилинейной поляре точки ).

Кубики

Кубика — это кривая третьего порядка (задающаяся уравнением третьей степени). Многие замечательные кубики, связанные с треугольником, строятся следующим образом: фиксируется точка в плоскости (возможно, бесконечно удалённая). Тогда множество таких точек , что прямая проходит через эту точку, является описанной около треугольника кубикой (здесь — точка, изогонально сопряжённая ). Такие кубики проходят также через центры вписанной и вневписанных окружностей, а также через саму фиксированную точку и изогонально сопряжённую ей. [10]

Соотношения в треугольнике

Примечание: в данном разделе , , — это длины трёх сторон треугольника, и , , — это углы, лежащие соответственно напротив этих трёх сторон (противолежащие углы).

Неравенство треугольника

В невырожденном треугольнике сумма длин двух его сторон больше длины третьей стороны, в вырожденном — равна. Иначе говоря, длины сторон треугольника связаны следующими неравенствами:

Неравенство треугольника является одной из аксиом метрики.

Теорема о сумме углов треугольника

Теорема синусов

где R — радиус окружности, описанной вокруг треугольника. Из теоремы следует, что если a Теорема косинусов

Источник