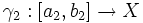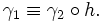Как называется плоская замкнутая кривая
Замкнутая плоская кривая, все точки которой одинаково удалены от её центра
Последняя бука буква «ь»
Ответ на вопрос «Замкнутая плоская кривая, все точки которой одинаково удалены от её центра «, 10 (десять) букв:
окружность
Альтернативные вопросы в кроссвордах для слова окружность
Определение слова окружность в словарях
Примеры употребления слова окружность в литературе.
Иные алгебраисты, люди, во все времена крайне необходимые обществу, вероятно, тут же схватятся за перья и, проделав вычисления, придут к следующему неоспоримому выводу: поскольку в обитателе системы Сириуса господине Микромегасе от пяток до макушки двадцать четыре тысячи шагов, что составляет сто двадцать тысяч футов, а мы, земные жители, редко бываем выше пяти футов, и поскольку окружность нашей планеты составляет девять тысяч лье, то, следовательно, планета, откуда он происходит, по окружности в двадцать Дин миллион шестьсот тысяч раз больше нашей крохотной Земли.
По окружности скафандра располагался балластный резервуар, придававший ему необходимую положительную или отрицательную плавучесть.
В то время, когда мы занима-емся медитацией во время пения зикра, возможны различные типы визуализации, например, во время вращательного движения почувствовать, что тело вычерчивает окружность.
В начальной стадии возникает закупорка выводного протока сальной железы, появляется припухлость и воспалительная краснота в окружности.
Трехсотлитровая бочка с приклепанной внутри трубой, похожая на гигантский самовар, была водружена на треногу в центре запасной гидрологической палатки, которую предварительно очистили от наледи, застелили брезентом, устлали досками и фанерными листами, а по окружности поставили высокие ящики-полки.
Источник: библиотека Максима Мошкова
Линия
Линия — это геометрическая фигура, образованная множеством точек, последовательно расположенных друг за другом.
Любую линию можно представить как след от точки, перемещающейся по данному пути. Например, грифель карандаша при прикосновении к бумаге оставляет на ней точку (1), но если грифелем провести по бумаге, то получится линия — последовательность точек, расположенных друг за другом (2):
Геометрические линии не имеют толщины.
Виды линий
Геометрические линии делятся на три вида:
| Вид линии | Пример |
|---|---|
| Прямая | |
| Неплоские кривые | |
| Винтовая линия • Линия откоса • Локсодрома • Ортодромия • Губка | |
| Связанные понятия | |
| Определения кривой | Аналитическая кривая • Кривая Жордана • Канторова кривая • Кривая Урысона |
| Преобразованные кривые | Эволюта • Эвольвента • Каустика |
Полезное
Смотреть что такое «Плоская кривая» в других словарях:
плоская кривая — кривая, все точки которой лежат в одной плоскости. Существуют следующие аналитические способы задания плоских кривых в декартовых координатах: F(х, у) = 0 (в неявном виде); у = f(х) (в явном виде); х = φ(t), у = Ψ(t) (в параметрическом виде). * * … Энциклопедический словарь
плоская кривая — plokščioji kreivė statusas T sritis fizika atitikmenys: angl. plane curve vok. Flachkurve, f rus. плоская кривая, f pranc. courbe plane, f … Fizikos terminų žodynas
Плоская кривая — кривая, все точки которой лежат в одной плоскости. Существуют следующие аналитические способы задания П. к.: 1) в декартовых координатах: F(x, у) = 0 (в неявном виде), у = f(x) (в явном виде), х = φ(t), у = ψ(t) (в параметрическом виде);… … Большая советская энциклопедия
ПЛОСКАЯ КРИВАЯ — кривая, все точки к рой лежат в одной плоскости. Существуют след. аналитич. способы задания П. к. в декартовых координатах: F(x, y)=0 (в неявном виде); y = f(x) (в явном виде); x = ф(t), y = фи(t) (в параметрич. виде) … Естествознание. Энциклопедический словарь
Роза (плоская кривая) — У этого термина существуют и другие значения, см. Роза (значения). Общий вид полярной розы при различных значениях k Роза плоская кривая, напоминающее символическое изображение цвет … Википедия
Гипербола (плоская кривая) — Гипербола. ГИПЕРБОЛА (от греческого hyperbole преувеличение), плоская кривая, разность расстояний любой точки М которой до двух данных точек F1 и F2 (фокусов) постоянна. … Иллюстрированный энциклопедический словарь
Жезл (плоская кривая) — У этого термина существуют и другие значения, см. Жезл (значения). Кривая „жезл“ Жезл плоская трансцендентная кривая, определяемая уравнением (в полярной … Википедия
Кривая Жордана — Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия
КРИВАЯ — (линия), след, оставленный движущейся точкой или телом. Обычно кривую представляют лишь как плавно изгибающуюся линию, вроде параболы или окружности. Но математическое понятие кривой охватывает и прямую, и фигуры, составленные из отрезков прямых … Энциклопедия Кольера
Кривая
Кривая или линия — геометрическое понятие, определяемое в разных разделах математики различно.
Содержание
Элементарная геометрия
В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки. Например, в «Началах» Евклида она определялась как «длина без ширины», также иногда её определяли как «границу фигуры».
Определение в топологии
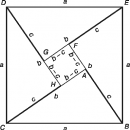
Чаще всего кривая определяется как непрерывное отображение из отрезка в пространство:
При этом, кривые могут быть различными, даже если их образы совпадают. Такие кривые называют параметризованными кривыми или, если 
Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые

эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) 


Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.
Комментарий
Приведённое определение во многом позволяет передать наше интуитивное представление о кривой как о чём-то, «нарисованном без отрыва карандаша». Однако это определение является слишком слабым, поскольку ему удовлетворяют многие фигуры, которые трудно считать кривыми.
Например, возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат (см. кривая Пеано ). Более того, согласно теореме Мазуркевича, любое компактное связное и локально связное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.
Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.
Кривая Жордана
Определение в анализе
В математическом анализе часто используется определение гладкой кривой. Определим сначала плоскую кривую (то есть кривую в 





Это определение можно обобщить на отображения в другие пространства, а также на отображения другого класса гладкости, см. ниже.
Определение в дифференциальной геометрии
Гладкие кривые 



Алгебраическая кривая
Алгебраические кривые изучаются в алгебраической геометрии. Плоская алгебраическая кривая — это множество точек с координатами x, y, задаваемое множество решений уравнения f(x, y) = 0, где f — многочлен от двух переменных с коэффициентами в поле F. В алгебраической геометрии обычно принимают во внимание не только точки, координаты которых принадлежат F, но и точки с координатами в алгебраическом замыкании F. Если C — плоская алгебраическая кривая кривая, такая что коэффициенты определяющего её многочлена лежат в поле F, она назывется кривой, определённой над F. Точки кривой, определённой над F, все координаты которых принадлежат G, называются рациональными над G (или просто G-точками). Пример: кривая x 2 + y 2 + 1 = 0, определённая над действительными числами, имеет точки, однако ни одна из них не является действительной точкой.
Алгебраические кривые можно определить и в пространствах большей размерности ; они определяются как множество решений системы полиномиальных уравнений.
после раскрытия скобок упрощается до однородного многочлена f(x, y, z) степени d. Значения x, y, z, такие что f(x, y, z) = 0 — однородные координаты пополнения плоской кривой, при этом точки исходной кривой — это точки, для которых z не равно нулю. Пример: кривая Ферма x n + y n = z n в аффинной форме принимает вид x n + y n = 1. Процесс перехода от аффинной кривой к проективной можно обобщить и на более высокие размерности.
Типы кривых
Типы точек на кривой
Обобщённые кривые
Более общее определение кривой для случая плоскости было дано Кантором в 1870-e годы:
Впоследствии это определение было обобщено Урысоном :
Кривой Урысона называется связное компактное топологическое пространство 
Ковёр Серпинского удовлетворяет этому определению, так что всякая канторова кривая является также и кривой Урысона. Обратно, если плоский связный компакт является кривой Урысона, то он будет канторовой кривой.
См. также
Литература
Ссылки
Аналитическая • Жордана • Канторова • Урысона • Овал • Спрямляемая
Эволюта • Эвольвента • Подера • Антиподера • Параллельная • Дуальная • Каустика
Винтовая линия • Линия откоса • Локсодрома • Ортодромия • Губка
Эллиптические : Эллиптическая кривая • Функции Якоби • Интеграл • Функции
Другие: Верзьера Аньези • Декартов лист • Полукубическая парабола • Строфоида • Циссоида Диокла
Бернулли ( Овал Кассини ) • Бута • Жероно
Сплайн ( B-сплайн • Кубический • Моносплайн • Эрмита ) • Безье
Кардиоида • Нефроида • Дельтоида • Астроида • Улитка Паскаля
Архимедова ( Ферма ) • Гиперболическая • «Жезл» • Клотоида • Логарифмическая
Квадратриса • Погони ( Трактриса ) • Трохоида • Цепная линия (перевёрнутая арочная ) • Постоянной ширины • Синусоида
Коха • Леви • Минковского • Пеано
Салфетка + Ковёр Серпинского • Губка Менгера
КРИВАЯ
КРИВАЯ (линия), след, оставленный движущейся точкой или телом. Обычно кривую представляют лишь как плавно изгибающуюся линию, вроде параболы или окружности. Но математическое понятие кривой охватывает и прямую, и фигуры, составленные из отрезков прямых, например, треугольник или квадрат.
Кривые можно разделить на плоские и пространственные. Плоская кривая, например, парабола или прямая, образуется при пересечении двух плоскостей или плоскости и тела и поэтому целиком лежит в одной плоскости. Пространственную кривую, например, винтовую линию, имеющую форму спиральной пружины, нельзя получить как пересечение какой-нибудь поверхности или тела с плоскостью, и она не лежит в одной плоскости. Кривые можно также подразделить на замкнутые и открытые. Замкнутая кривая, например квадрат или окружность, не имеет концов, т.е. движущаяся точка, порождающая такую кривую, периодически повторяет свой путь.
Кривая есть геометрическое место, или множество, точек, удовлетворяющих некоторому математическому условию или уравнению. Например, окружность – это геометрическое место точек плоскости, равноудаленных от данной точки. Кривые, определяемые алгебраическими уравнениями, называются алгебраическими кривыми. Например, уравнение прямой y = mx + b, где m – угловой коэффициент, а b – отрезок, отсекаемый на оси y, – алгебраическое. Кривые, уравнения которых содержат трансцендентные функции, например, логарифмы или тригонометрические функции, называются трансцендентными кривыми. Например, y = log x и y = tg x – уравнения трансцендентных кривых.
Форму алгебраической кривой можно определить по степени ее уравнения, которая совпадает с наивысшей степенью членов уравнения. Если уравнение первой степени, например Ax + By + C = 0, то кривая имеет форму прямой. Если уравнение второй степени, например, Ax 2 + By + C = 0 или Ax 2 + By 2 + C = 0, то кривая квадратична, т.е. представляет собой одно из конических сечений; к числу таких кривых относятся параболы, гиперболы, эллипсы и окружности. Перечислим общие формы уравнений конических сечений: x 2 + y 2 = r 2 (окружность), x 2 /a 2 + y 2 /b 2 = 1 (эллипс), y = ax 2 (парабола), x 2 /a 2 – y 2 /b 2 = 1 (гипербола). Кривые, соответствующие уравнениям третьей, четвертой, пятой, шестой и т.д. степеней, называются кривыми третьего, четвертого, пятого, шестого и т.д. порядка. Как правило, чем выше степень уравнения, тем больше изгибов будет у открытой кривой.
Многие сложные кривые получили специальные наименования. Циклоидой называется плоская кривая, описываемая фиксированной точкой окружности, катящейся по прямой, называемой образующей циклоиды; циклоида состоит из серии повторяющихся дуг. Эпициклоида – это плоская кривая, описываемая фиксированной точкой окружности, катящейся по другой неподвижной окружности вне ее. Гипоциклоидой называется плоская кривая, описываемая фиксированной точкой окружности, катящейся изнутри по неподвижной окружности. Спиралью называется плоская кривая, которая виток за витком раскручивается от неподвижной точки (или накручивается на нее).
Математики занимались изучением свойств кривых с глубокой древности, и названия многих необычных кривых связаны с именами тех, кто впервые их исследовал. Таковы, например, спираль Архимеда, локон Аньези, циссоида Диоклеса, кохоида Никомеда и лемниската Бернулли. См. также АБСТРАКТНЫЕ ПРОСТРАНСТВА; АЛГЕБРАИЧЕСКАЯ ГЕОМЕТРИЯ; АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ; КОНИЧЕСКИЕ СЕЧЕНИЯ; ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ; ФУНКЦИЯ; ГЕОМЕТРИЯ; ТОПОЛОГИЯ.







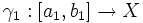 и
и