в шкале интервалов нельзя сравнить значения по величине
Интервальные шкалы
Интервальная шкала является третьей по уровню измерения переменных. В отличие от порядковой шкалы она является шкалой с равными интервалами. Разница между двумя значениями шкалы идентична разнице между двумя любыми другими смежными значениями интервальной шкалы. Это позволяет осуществлять количественное сравнение значений переменной, т. е. можно определить, насколько одно значение больше или меньше (хуже или лучше) другого.
Пример 11. Если IQ Ивана равен 80, у Петра — 120 и у Александра — 160, можно сказать, что Петр по сравнению с Иваном настолько же интеллектуальнее, насколько Александр по сравнению с Петром (а именно на 40 единиц IQ). Однако, основываясь только на том, что значение IQ у Ивана в два раза меньше, чем у Александра, исходя из определения IQ, нельзя сделать вывод, что Александр вдвое умнее Ивана.
У интервальной шкалы отсутствует “естественный нуль”, т. е. исходная точка измерения является относительной. Эта шкала позволяет применять для анализа данных практически все статистические методы. Помимо медианы и моды для характеристики центральной тенденции используется среднее арифметическое, а для оценки разброса — дисперсия. Для оценки величины статистической связи между переменными применяется коэффициент линейной корреляции Пирсона.
В маркетинговых исследованиях интервальные шкалы часто используются при обработке данных, полученные по рейтинговым шкалам.
Относительные шкалы
Относительная шкала характеризуется самым высоким уровнем измерения переменных. Она обладает всеми свойствами номинальной, порядковой и интервальной шкал и, кроме того, имеет точку начала отсчета, “естественный нуль”. Относительная шкала позволяет сравнивать значения переменной по отношению друг к другу, что невозможно при использовании интервальной шкалы. Например, прибыль в 1000 млн руб. в два раза меньше, чем прибыль 2000 млн руб.
Эта шкала используется для измерения количественных характеристик объекта исследования: объема, роста, веса, возраста, скорости, дохода, объем продаж и т. д. При анализе данных, измеренных по относительной шкале, можно использовать все статистические методы анализа.
Виды шкал и их особенности
Проблема обеспечения высокого качества продукции тесным образом связана с проблемой качества измерений. Между ними явно прослеживается непосредственная связь: там, где качество измерений не соответствует требованиям технологического процесса, невозможно достичь высокого уровня качества продукции. Поэтому качество продукции в значительной степени зависит от успешного решения вопросов, связанных с точностью измерений параметров качества материалов и комплектующих изделий и поддержания заданных технологических режимов. Иными словами, технический контроль качества осуществляется путем замеров параметров технологических процессов, результаты измерений которых необходимы для регулирования процессом.
Следовательно, качество измерений представляет собой совокупность свойств состояния измерений, обеспечивающих результаты измерений с требуемыми точностными характеристиками, получаемые в необходимом виде за определенный отрезок времени.
Основные свойства состояния измерений:
• точность результатов измерений;
• воспроизводимость результатов измерений;
• сходимость результатов измерений;
• быстрота получения результатов;
При этом под воспроизводимостью результатов измерений понимается близость результатов измерений одной и той же величины, полученные в разных местах, разными методами, разными средствами, разными операторами, в разное время, однако в одних и тех же условиях измерений (температуре, давлении, влажности и т.д.).
Сходимость результатов измерений — это близость результатов измерений одной и той же величины, проведенных повторно с применением одних и тех же средств, одним и тем же методом в одинаковых условиях и с той же тщательностью.
Любое измерение или количественное оценивание чего-либо осуществляется, используя соответствующие шкалы.
Шкала — это упорядоченный ряд отметок, соответствующий соотношению последовательных значений измеряемых величин. Шкалой измерений называется принятая по соглашению последовательность значений одноименных величин различного размера.
В метрологии шкала измерений является средством адекватного сопоставления и определения численных значений отдельных свойств и качеств различных объектов. Практически используют пять видов шкал: шкалу наименований, шкалу порядка, шкалу интервалов, шкалу отношений и шкалу абсолютных значений.
Шкала наименований (номинальная шкала). Это самая простая из всех шкал. В ней числа выполняют роль ярлыков и служат для обнаружения и различения изучаемых объектов. Числа, составляющие шкалу наименований, разрешается менять местами. В этой шкале нет отношений типа «больше—меньше», поэтому некоторые полагают, что применение шкалы наименований не стоит считать измерением. При использовании шкалы наименований могут проводится только некоторые математические операции. Например, ее числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.
Шкала порядка. Места, занимаемые величинами в шкале порядка, называются рангами, а сама шкала называется ранговой, или неметрической. В такой шкале составляющие ее числа упорядочены по рангам (т.е. занимаемым местам), но интервалы между ними точно измерить нельзя. В отличие от шкалы наименований шкала порядка позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства в виде суждений: «больше—меньше», «лучше—хуже» и т.п.
С помощью шкал порядка можно измерять качественные, не имеющие строгой количественной меры, показатели. Особенно широко эти шкалы используются в гуманитарных науках: педагогике, психологии, социологии. К рангам шкалы порядка можно применять большее число математических операций, чем к числам шкалы наименований.
Шкала интервалов. Это такая шкала, в которой числа не только упорядочены по рангам, но и разделены определенными интервалами. Особенность, отличающая ее от описываемой дальше шкалы отношений, состоит в том, что нулевая точка выбирается произвольно. Примерами могут быть календарное время (начало летоисчисления в разных календарях устанавливалось по случайным причинам, температура, потенциальная энергия поднятого груза, потенциал электрического поля и др.).
Результаты измерений по шкале интервалов можно обрабатывать всеми математическими методами, кроме вычисления отношений. Данные шкалы интервалов дают ответ на вопрос «на сколько больше?», но не позволяют утверждать, что одно значение измеренной величины во столько-то раз больше или меньше другого. Например, если температура повысилась с 10 до 20°С, то нельзя сказать, что стало в два раза теплее.
Шкала отношений. Эта шкала отличается от шкалы интервалов только тем, что в ней строго определено положение нулевой точки. Благодаря этому шкала отношений не накладывает никаких ограничений на математический аппарат, используемый для обработки результатов наблюдений.
По шкале отношений измеряют и те величины, которые образуются как разности чисел, отсчитанных по шкале интервалов. Так, календарное время отсчитывается по шкале интервалов, а интервалы времени — по шкале отношений.
При использовании шкалы отношений (и только в этом случае!) измерение какой-либо величины сводится к экспериментальному определению отношения этой величины к другой подобной, принятой за единицу. Измеряя длину объекта, мы узнаем, во сколько раз эта длина больше длины другого тела, принятого за единицу длины (метровой линейки в данном случае) и т.п. Если ограничиться только применением шкал отношений, то можно дать другое (более узкое, частное) определение измерения: измерить какую-либо величину — значит найти опытным путем ее отношение к соответствующей единице измерения.
Шкала абсолютных величин. Во многих случаях напрямую измеряется величина чего-либо. Например, непосредственно подсчитывается число дефектов в изделии, количество единиц произведенной продукции, сколько студентов присутствует на лекции, количество прожитых лет и т.д. и т.п. При таких измерениях на измерительной шкале отмечаются
абсолютные количественные значения измеряемого. Такая шкала абсолютных значений обладает и теми же свойствами, что и шкала отношений, с той лишь разницей, что величины, обозначенные на этой шкале, имеют абсолютные, а не относительные значения.
Результаты измерений по шкале абсолютных величин имеют наибольшую достоверность, информативность и чувствительность к неточностям измерений.
Шкалы интервалов, отношений и абсолютных величин называются метрическими, так как при их построении используются некоторые меры, т.е. размеры, принятые в качестве единиц измерений.
В шкале интервалов нельзя сравнить значения по величине
Шкала интервалов очень часто используется исследователями. Классическим примером применения этой шкалы в физике является измерение температуры по Цельсию. Шкала интервалов имеет масштабную единицу, но положение нуля на ней произвольно, поэтому нет смысла говорить, во сколько раз больше или меньше утренняя температура воздуха, измеренная шкалой Цельсия, чем дневная.
Интервальная шкала позволяет применять практически всю параметрическую статистику для анализа данных, полученных с ее помощью. Помимо медианы и моды для характеристики центральной тенденции используется среднее арифметическое, а для оценки разброса—дисперсия. Можно вычислять коэффициенты асимметрии и эксцесса и другие параметры распределения. Для оценки величины статистической связи между переменными применяется коэффициент линейной корреляции Пирсона и т.д.
Большинство специалистов по теории психологических измерений полагают, что тесты измеряют психические свойства с помощью шкалы интервалов. Прежде всего, это касается тестов интеллекта и достижений. Численные значения одного теста можно переводить в численные значения другого теста с помощью линейного преобразования: х’ = ах + b.
Скорее всего, шкала любого теста интеллекта является комбинированной шкалой, с естественным минимумом иили максимумом, но порядковой. Однако эти соображения не мешают тестологам рассматривать шкалу IQ как интервальную, преобразуя «сырые» значения в шкальные с помощью известной процедуры «нормализации» шкалы.(2, 3)
Шкала отношений
Шкалу отношений называют также шкалой равных отношений. Особенностью этой шкалы является наличие твердо фиксированного нуля, который означает полное отсутствие какого-либо свойства или признака. Шакала отношений является наиболее информативной шкалой, допускающей любые математические операции и использование разнообразных статистических методов.
Шкала отношений по сути очень близка интервальной, поскольку если строго фиксировать начало отсчета, то любая интервальная шкала превращается в шкалу отношений.
Шкала отношений показывает данные о выраженности свойств объектов, когда можно сказать, во сколько раз один объект больше или меньше другого.
Именно в шкале отношений производятся точные и сверхточные измерения в таких науках, как физика, химия, микробиология и др. Измерение по шкале отношений производятся и в близких к психологии науках, таких, как психофизика, психофизиология, психогенетика. (4).
Отличием этой шкалы от абсолютной является отсутствие «естественной» масштабной единицы.
Другие шкалы
В психологии абсолютные шкалы не используются. Данные, полученные с помощью абсолютной шкалы, не преобразуются, шкала тождественна сама себе. Любые статистические меры допустимы.
4. В литературе, посвященной проблемам психологических измерений, упоминаются и другие типы шкал: ординальная (порядковая) с естественным началом, логинтервальная, упорядоченная метрическая и др.
Все написанное выше относится к одномерным шкалам. Шкалы могут быть и многомерными: шкалируемый признак в этом случае имеет ненулевые проекции на два (или более) соответствующих параметра. Векторные свойства, в отличие от скалярных, являются многомерными. (2, 3).
Шкала интервалов, примеры
Вы будете перенаправлены на Автор24
Что такое шкала интервалов?
Шкала интервалов – это метрическая шкала, определяющая размер и количество отличий между объектами в выражении их особенностей, качеств.
Такая шкала открывает возможности определения не только отличительных характеристик объектов, но и их количество в проявлении того или иного свойства объекта. Она составляет группировки объектов по признаку большего, либо меньшего размера на конкретное количество единиц. Над существующими измерениями допускается производить разнообразные арифметические операции.
Построение данной шкалы базируется на ведущем понятии – интервал. Он представляет собой размер диагностируемого показателя качества между двумя, рядом находящимися позициями, занимающими шкалу интервалов.
Каждый интервал характеризуется определенным размером. Размер интервала является постоянным и не может быть изменен ни на одном участке шкалы. Для определения интервального размеры осуществляется установка единиц измерения. Для этого, объекту или качеству дается число, которое отражает количество единиц измерения, равноценное размеру, имеющегося качества.
Шкала интервалов не располагает точкой отсчета т.е. нулевой отметки, свидетельствующей об отсутствии измеряемого признака не имеется. Точнее, нуль на шкале присутствует, но является условным показателем.
Целевым назначением шкалы интервалов является проведение сравнительной характеристики двух объектов или процессов, с определением преобладания определенного признака или качества у одного из них.
Проведение анализа различных процессов и явлений с применением интервальной шкалы дает возможности использования любого рода статистических методов. Можно применять приемы дисперсии, методы определения среднего арифметического, чтобы охарактеризовать приоритетную тенденцию развития.
Готовые работы на аналогичную тему
Рисунок 1. Шкала интервалов. Автор24 — интернет-биржа студенческих работ
Существует два основных вида интервальных шкал:
Применение шкалы актуально для определения уровней проявления разнообразных свойств психического и физиологического характера, определения и сравнения температурных показателей, проведения оценочной статистики в образовательной системе, оценки спортивных мероприятий, результатов спортивных игр, учебных и спортивных достижений.
В основе применения шкалы лежит следующий статистический аппарат:
Типичные примеры применения интервальных шкал
Применение шкалы интервалов актуально тогда, когда не имеет значения во сколько раз больше или меньше определенный показатель, параметр, свойство объекта или процесса. Это касается температурных шкал. Например, шкала измерения температуры воздуха по Цельсию или по Фаренгейту строится именно по принципу интервалов. Она призвана показать температуру воздуха в данный временной промежуток, не отражая данные о том, во сколько раз отличается утренняя температура от вечерней, дневная от утренней и т.д.
Рисунок 2. Шкалы интервалов. Автор24 — интернет-биржа студенческих работ
Распространено применение интервальных шкал в психологии. Шкала позволяет измерять различные психологические особенности личности, ее взгляды, социальные установки, ценностные ориентиры. Кроме того, применяются тестовые шкалы, построенные на базе метричности измерений. Например, это тесты IQ, T-шкала. При этом, многие ученые подвергают сомнению возможность применения интервалов для определения уровня интеллекта. Это объясняется тем, что любой тестируемый может получить нулевой был при невыполнении задания или же, напротив, максимальный балл при его полном и быстром выполнении. Также, отдельные значения шкалы имеют неодинаковую разницу.
Шкалы интервалов используются также для составления календарей, независимо от избранной точки отсчета летоисчисления. Это может быть, как дата сотворения мира, рождество Христово, день рождения первого человека на Земле, так и иное значимое событие.
Применение шкалы интервалов особенно актуально при проведении опросов. Ее использование помогает определить отношение респондента к конкретной проблеме, теме, вопросу. При этом ее построение зависит от конкретной тематики опроса, его содержания и целевого назначения. Здесь, важное значение имеет построение оптимальной шкалы интервалов, которое не будет содержать избыточного или недостаточного количества интервалов.
Шкалы интервалов могут иметь следующий вид:
Рисунок 3. Шкала интервалов. Автор24 — интернет-биржа студенческих работ
В системе образования, применение шкал интервалов возможно для оценивания интенсивности формирования того или иного свойства у ребенка (получение определенного навыка, формирование дисциплинированности, развитие творческих способностей и т.д.), оценки степени его подготовленности по определенной теме, дисциплине, курсу. При этом, по данной шкале невозможно сопоставить учащихся и их достижения в процентном отношении друг к другу. Например, если за выполнение творческой работы Петров получил оценку 5, а Иванов оценку 3, то мы не можем сказать во сколько раз творческие способности Петрова оказались более развитыми, чем Иванова.
Затруднения в применении шкал интервалов в системе образования связаны с тем, что достаточно проблематично доказать равенство между всеми, имеющимися пунктами шкалы.
Шкалы интервалов применяются в маркетинговых исследованиях, в комплексе с показателями рейтинговых шкал. В данном случае, параметры, полученные по рейтинговой шкале проходят обработку с помощью шкалы интервалов.
При использовании интервальных шкал, любые тестовые заключения носят относительный характер. Они зависят от параметров той выборки, в которой производилась стандартизация теста.
В шкале интервалов нельзя сравнить значения по величине
Во многих случаях нет возможности измерить сами величины наблюдаемых размеров, но возможно (если есть необходимость) измерять только отличия (разницы) между познаваемыми сопоставлением размерами. При этом используется так называемая шкала интервалов.
На измерительной шкале интервалов фиксируются отличия сопоставляемых размеров. Эта форма отображения величин измеряемого является более совершенной, так как на шкале интервалов есть условные, но вполне определенные единицы измерений, что позволяет количественно (численно) охарактеризовать соотношение исследуемых размеров.
Математическая запись сравнения между собой двух однородных размеров по их разнице имеет вид
По шкале интервалов определяют такие соотношения размеров, как: равно (=), не равно (≠), больше (>), меньше (
Следовательно, здесь определено отношение порядка и эквивалентности не только между размерами характеристик качества, но и между расстояниями между ними на шкале измерений.
Упорядоченные ряды, например, пяти разных размеров по их 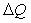
или ∆Q4,3 > ∆Q3,5 > ∆Q2,5 > ∆Q1,2.
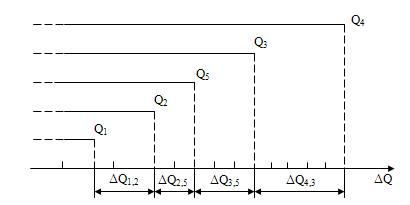
Графическое построение шкалы интервалов рассматриваемых размеров показано на рис. 2.1.
Рис.2.1. Схема построения шкалы интервалов
При таком построении шкалы интервалов, когда нет начала отсчета и нет соответствующей физической единицы измерений (меры), за единицу измерений принимается некоторая произвольно выбранная величина. Несмотря на значительную неопределенность измеряемых разностей размеров в условных единицах, результаты измерений по шкале интервалов более информативны по сравнению с измерениями по шкале порядка, так как они позволяют не только установить, что один размер больше или меньше другого, но и численно определить, на сколько единиц (мер) отличаются исследуемые размеры один от другого.
С данными, полученными по шкале интервалов, можно производить не только логические, но и арифметические действия, например, складывать и вычитать величины. Однако по шкале интервалов нельзя определить, во сколько раз данный размер больше или меньше другого, так как неизвестными остаются величины сопоставляемых размеров.
Часто при решении измерительной задачи требуется более жесткая «привязка» результатов, получаемых по шкале интервалов, к определенному (произвольно выбранному или предпочтительному) размеру. Этот выбранный размер является опорным (базовым), по сравнению с которым определяют отличия других размеров. Отметка базового размера на измерительной шкале (линейной, круговой или цифровой) представляет собой реперную точку. Эта реперная точка, если она одна на шкале интервалов, обычно принимается за начало отсчетов.
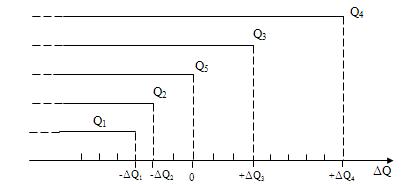
На рис. 2.2 иллюстрировано построение шкалы интервалов с началом отсчета от размера Q5.
Рис. 2.2 Построение шкалы интервалов с нулевой отметкой
Примерами шкал интервалов с одной реперной точкой являются календари летоисчислений. В христианском календаре за нулевую точку отсчета принят год рождения Христа («от рождества Христова»).
Зачастую. с целью приближения единицы измерений по шкале интервалов к реальности, за меру измеряемых интервалов берут долю и некоторую часть чего-либо (предпочтительного) интервала размеров. Для этого на шкале измерений устанавливаю две реперные точки Qp1 и Qp2, расстояние между которыми выражает разницу двух выбранных размеров. Промежуток между реперными точками градируется, т.е. делится на равные или (реже) пропорциональные части.
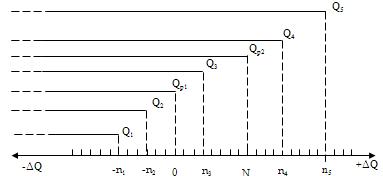
Схема создания такой двухреперной шкалы интервалов приведена на рис. 2.3.
Рис.2.3. Шкала интервалов с двумя реперными точками
Классическим примером измерений по шкале интервалов с двумя реперными точками является измерение температур по шкале Цельсия. Здесь в качестве опорных размеров взяты температуры замерзания (таяния льда) и кипения чистой воды. Интервал между этими температурами разделены на 100 равных частей. Одна часть, принятая за единицу измерения температур, была названа градусом. Шкала Цельсия неограниченно распространяется за пределы температур 0% 100°С при условии, что любые значения температур измеряются единицами, равными 1/100 части интервала температур от замерзания до кипения воды.
Шкала интервалов может иметь и несколько реперных точек, но в этом случае возникает проблема согласования единиц измерения размеров в пределах различных интервалов такой многореперной шкалы.
Ввиду неопределенности или условности начала отсчета математические операции умножения и деления результатов измерений, полученных с помощью шкал интервалов, осуществить нельзя. Следовательно, по шкале интервалов нет возможности определить, во сколько раз один размер больше или меньше другого.
Для того чтобы определить не только на сколько, но и во сколько раз один размер больше или меньше другого, или количественно измерить величину размера в официально выбранных единицах измерения, необходимо воспользоваться шкалой отношений.
В метрологии и квалиметрии считается, что «любое измерение по шкале отношений предполагает сравнение неизвестного размера с известным и выражение первого через второй в кратном или дольном отношении».
Математическая запись измерения по шкале отношений имеет вид:
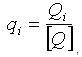
По шкале отношений определяются такие значения измеряемых размеров, как: равно (=), не равно (≠), больше (>), меньше (
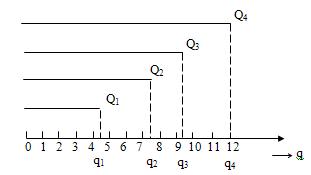
Рис. 2.4. Схема измерений по шкале отношений
Так как со qi значениями возможны логические и все арифметические операции: сложение, вычитание, умножение, деление, поэтому шкала отношений является наиболее совершенной и широко применяемой. Однако построение шкалы отношений и измерение с ее помощью не всегда возможны. Например, время измеряется только по шкале интервалов, а вес обычно измеряется по шкале отношений, хотя его можно измерить и по шкале интервалов, так как шкала отношений является частным случаем шкалы интервалов.
Измерение интервала по шкале отношений осуществляют по формуле (теоретической модели) вида:
Итак, шкала отношений универсальна, так как по ней можно сформировать ранжированные ряды (шкалы порядка) возрастающих или сокращающихся размеров, вычислить интервалы отличий (как и по шкале интервалов) тех размеров, которые измерены по шкале отношений и, наконец, определить численные значения измеренных размеров в относительных величинах.
Шкала отношений наиболее приемлема для измерений большинства показателей качества, особенно для таких численных характеристик, как геометрические размеры объектов, их плотность, сила, напряжение, частота колебаний и прочие.