То что в теореме дано можно назвать
Что такое аксиома, теорема и доказательство теоремы
Понятие аксиомы
Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.
Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.
Синоним аксиомы — постулат. Антоним — гипотеза.
Основные аксиомы евклидовой геометрии
Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.
А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.
Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:
Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.
У этой аксиомы два следствия:
Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:
Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.
На картинке можно увидеть, как это выглядит:
Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.
Понятие теоремы
Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.
Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.
Состав теоремы: условие и заключение или следствие.
Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.
Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.
Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.
Примеры следствий из аксиомы о параллельности прямых:
Доказательство теоремы — это процесс обоснования истинности утверждения.
Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.
Способы доказательства геометрических теорем
Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.
Приемы для доказательства в геометрии:
Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.
Прямая и обратная теорема взаимно-обратные. Например:
В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.
Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.
Вот, как выглядит взаимное отношение теорем на примере:
В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.
Записывайся на онлайн обучение по математике для учеников с 1 по 11 классы!
Доказательство через синтез
Рассмотрим пример синтетического способа доказательства.
Теорема: сумма углов треугольника равна двум прямым.
Дан треугольник: ABC. Нужно доказать, что A + B + C = 2d.
Доказательство:
Проведем прямую DE, так чтобы она была параллельна AC.
Сумма углов, лежащих по одну сторону прямой, равна двум прямым, следовательно, α + B + γ = 2d.
Так как α = A, γ = C, то заменим в предыдущем равенстве углы α и γ равными им углами: A + B + C = 2d. Что и требовалось доказать.
Здесь исходным предложением в цепи доказательств выбрана теорема о сумме углов, которые лежат по одну сторону прямой. Есть связь с теоремами о равенстве углов накрест-лежащих при пересечении двух параллельных третьею косвенною. Доказываемая теорема есть необходимое следствие всех предложенных теорем и является в цепи доказательств последним заключением.
Доказательство через анализ
Рассмотрим пример аналитического способа доказательства.
Теорема: диагонали параллелограмма пересекаются пополам.
Дан параллелограмм: ABCD.
Доказательство:
Если диагонали пересекаются пополам, то треугольники AOB и DOC равны.
Равенство же треугольников AOB и DOC вытекает из того, что AB = CD, как противоположные стороны параллелограмма и ∠α = ∠γ, ∠β = ∠δ, как накрест-лежащие углы.
Таким образом мы видим, что последовательно данное предложение заменяется другим и такое замещение совершается до тех пор, пока не дойдем до уже доказанного предложения.
Теоремы без доказательств
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:
Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:
где a, b и c — стороны плоского треугольника,
α — угол напротив стороны а.
Следствия из теоремы косинусов:
Понятия свойств и признаков
У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.
Свойства и признаки — понятия из обычной жизни, которые мы часто используем.
Свойство — такое утверждение, которое должно выполняться для данного типа объектов. У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.
Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны. Это верно для любого квадрата, поэтому это — свойство.
Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.
Признак — это то, по чему мы однозначно распознаем объект.
Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.
А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AB = BD = 10 см.
Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AB = BD, диагонали равны, но он не является прямоугольником. Это свойство, но не его признак.
Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AB = BD, то это уже верный признак прямоугольника. Смотрите рисунок:
Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.
Такие утверждения называют необходимым и достаточным признаком.
02.3. Структура теоремы. Виды теорем
Структура теоремы. Виды теорем
Известно, что ТЕОРЕМА – это высказывание в теории, имеющее доказательство (то есть истинное в данной теории). Доказательство опирается на аксиомы, определения и другие теоремы. ТЕОРЕМА является формулой, выводимой в рамках построенной аксиоматической системы. При формулировке теоремы мы стараемся распространить определенное свойство на целую группу предметов или явлений, т. е. показать, что Любой объект из этой группы обладает отмеченной особенностью. Обычно теорема состоит из условия и заключения, которые связаны между собой логической операцией – импликацией. Вот почему, с точки зрения логической структуры, любая теорема есть высказывание вида:
Допустимы ли выражения: «Данная теорема неверна», «Проверим справедливость теоремы», «Эта теорема недоказуема»?
Это высказывание назовем ПРЯМОЙ ТЕОРЕМОЙ.
Используя правило контрпозиции, дадим определение.
Называется противоположной обратной для прямой теоремы 
(таблица 8а). Если при этом теоремой является высказывание 
, то оно называется обратной теоремой, а теорема
Называется противоположной теоремой. В этом случае имеет место следующий список теорем (табл. 8Б.)
Виды теорем и связь между ними.
Прямая и обратная теоремы связаны с понятиями НЕОБХОДИМОГО И ДОСТАТОЧНОГО УСЛОВИЙ. В прямой теореме присутствуют два предиката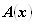 
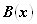
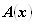
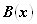
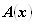
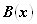
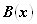
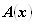
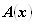
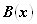
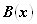
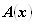
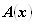
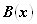
и 
, один из которых определяет Условие, другой – Вывод теоремы. В обратной теореме условие и вывод меняются местами. Поэтому, рассматривая прямую и обратную теоремы, предикаты и будем называть условиями. Если имеет место прямая теорема, то называют ДОСТАТОЧНЫМ УСЛОВИЕМ ДЛЯ , а – НЕОБХОДИМЫМ УСЛОВИЕМ ДЛЯ . Если же имеет место обратная теорема, то НАЗЫВАЮТ НЕОБХОДИМЫМ УСЛОВИЕМ ДЛЯ , а – ДОСТАТОЧНЫМ УСЛОВИЕМ ДЛЯ . Если, наконец, справедливы импликации, то есть 
, то условие НАЗЫВАЮТ НЕОБХОДИМЫМ И ДОСТАТОЧНЫМ УСЛОВИЕМ ДЛЯ .
Но ежели для истинной любви
страдание всегда необходимо,
То, видно, уж таков закон любви,
Научимся сносить его с терпением.
Итак, страдание – необходимое условие истинной любви. Можно ли считать это условие и достаточным?
В сущности, необходимое условие есть условие, истинность которого следует из истинности некоторого другого утверждения. Достаточное условие есть условие, из истинности которого следует истинность некоторого другого утверждения. Необходимое и достаточное условие есть соединение двух вышерассмотренных условий. Для его формулировки используют также словосочетания: «… тогда и только тогда …», «… в том и только в том случае …», «… если и только если …».
Следует различать противоположную теорему
И отрицание прямой теоремы
Из свойств кванторных операций следует:
.
Используя тавтологии 22 и 23, прямую теорему можно представить в виде:
А ее отрицание – следующим образом:
Эти соотношения полезны для понимания сути высказываний, определяющих прямую теорему и ее отрицание.
Редкий случай в математике: способом для иллюстрации рассуждений служат сами теоремы.
Обычно бывает наоборот.
ТЕОРЕМА ВИЕТА. Если приведенное квадратное уравнение
Введем предикаты 
: «Приведенное квадратное уравнение A: 
имеет корни х1 и х2» и 
: «В приведенном квадратном уравнении A Числа х1 и х2 удовлетворяют соотношениям:
».
Содержание теоремы определяется высказыванием
Считая эту теорему прямой, сформулируем обратное высказывание: 
, то есть
Если числа х1 и х2 таковы, что
То х1 и х2 – корни квадратного уравнения:
Как известно, оно является теоремой:
.
В силу существования обратной теоремы сформулируем противоположную теорему: 
.
ТЕОРЕМА. Если в приведенном квадратном уравнении
Числа х1 и х2 не являются корнями, то Хотя бы одно из равенств:
Выполняться не будет.
Теорему, противоположную обратной, 
сформулируем следующим образом:
ТЕОРЕМА. Если числа х1 и х2 таковы, что Хотя бы одно из равенств:
Не выполняется, то х1 и х2 не будут корнями квадратного уравнения
Она возможна, так как имеет место прямая теорема.
Прямая теорема может быть еще сформулирована на основании тавтологии 22 иначе.
ТЕОРЕМА. Или Хотя бы одно из чисел х1 и х2 не является корнем приведенного квадратного уравнения
Сформулируем отрицание прямой теоремы: «Неверно, что если приведенное квадратное уравнение
Имеет корни х1 и х2, то
.
Данное высказывание ложно, так как имеет место прямая теорема. Из тавтологии 23 следует, что оно эквивалентно следующему: «Существует такое приведенное квадратное уравнение
Что х1 и х2 – его корни и Хотя бы одно из равенств
Прямая и обратная теоремы, могут быть объединены в одну.
ТЕОРЕМА. Для того, чтобы действительные числа х1 и х2 были корнями приведенного квадратного уравнения
,
Необходимо и достаточно, чтобы выполнялись условия:
Рассмотрим еще одну теорему.
ТЕОРЕМА. Диагональ параллелограмма делит его на два равных треугольника.
Введем предикаты 
: «Четырехугольник 
– параллелограмм» и 
: «Диагональ делит четырехугольник на два равных треугольника». Тогда можно утверждать, что если четырехугольник – параллелограмм (предикат ), то этого условия достаточно для того, чтобы диагональ параллелограмма делила его на два равных треугольника. Сформулируем обратное высказывание.
«Если диагональ четырехугольника делит его на два равных треугольника, то этот четырехугольник – параллелограмм.
Оно неверно, что подтверждает контрпример на рис. 2.1. Поэтому условие не может быть необходимым, а – достаточным.
Тема: «Структура теорем. Виды теорем, связанных с данной теоремой»
Тема: «Структура теорем. Виды теорем, связанных с данной теоремой»
Цели: повышение качества образовательного процесса посредством применения современных образовательных технологий; изучить понятие теоремы, её структуру, виды теорем, связанных с данной;создать условия для формирования общих и профессиональных компетенций по теме занятия.
Междисциплинарные связи: методика математики, математика.
Материально-техническое обеспечение занятия: интерактивная доска, персональный компьютер, видеокамера, электронная презентация, учебники математики для начальной школы для 1, 2, 3, 4 классов по различным программам обучения, дидактические материалы: карточки, задания для практической работы по подгруппам, схема логического анализа теоремы, карточки для записи опорного конспекта «Запиши и запомни», карточки с примерами теорем, памятки с формируемыми общими и профессиональными компетенциями.
Организация начала занятия
Актуализация усвоения изученного материала. Слайды
Собрать листки с домашними заданиями. Провести фронтальный опрос по домашнему заданию. На доске два человека выполняют дифференцированные упражнения. Одновременно проходит работа на карточках с последующей самостоятельной проверкой( ключи с ответами выдаются студентам)
Определите значение истинности высказываний:
Число 6 делится на 2 и на 3.
б)Некоторые нечетные числа делятся на 5 ( 
Х – множество нечетных чисел
в) при делении 42 на 5 в остатке получится 2 или 5.
Карточка №2 Запишите предложение математическими символами:
Карточка №3Данные ниже высказывания взяты из учебника математики для начальных классов. Выясните, какие из них содержат квантор в явном или неявном виде:
а) От перестановки слагаемых сумма не изменяется;
б) Площадь прямоугольника равна произведению его длины на ширину;
в) Существуют четные числа;
г) Некоторые числа делятся на 4;
д) Среди многоугольников есть треугольники.
Карточка №4 Постройте отрицания следующих высказываний и высказывательных форм:
Некоторые однозначные числа делятся на 10 При делении числа 32 на 5 в остатке получится 7 Число 123 делится на 9 3+2 4; Треугольник АВС – прямоугольный.
Самопроверка и самооценка результатов своей работы. Итог.
Постановка темы и задач занятия.
Давайте подведем итог. О чем мы говорили, что изучали на предыдущих уроках? ( предложения). Сегодня мы также будем говорить о предложениях, ( утверждениях) но только о таких которые требуют доказательства.
Попробуйте сформулировать тему нашего урока.
Слайд. Тема нашего занятия «Структура теоремы. Виды теорем, связанных с данной».
Исходя из темы и плана, определим задачи нашего занятия.
Обобщить знания о понятии «теорема» и её структуре. Познакомиться с видами теорем, связанных с данной теоремой. Научиться определять структуру теорем и строить другие теоремы, связанные с данной. Выяснить, как связана изучаемая тема с преподаванием математики в начальной школе.
Изучение нового материала.
Теорема – это высказывание, истинность которого устанавливается посредством рассуждения (доказательства).
— У вас на столах есть карточки № 1 с формулировками различных теорем.
1) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
3) Сумма углов треугольника равна 1800.
4) Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
6) Равные многоугольники имеют равные площади.
8) Если число оканчивается на 0 или на 5, то оно делится на 5.
Что общего в этих формулировках? ( В каждой теореме есть то, что дано и то, что надо доказать)
1. Разъяснительная часть (описание множества, о котором идет речь в теореме);
2. Условие теоремы (то, что дано);
3. Заключение теоремы (то, что надо доказать).
Краткая логическая запись:
А 
В
Теорему удобно представлять в виде Если А, то В. Несмотря на то, что одну и ту же теорему можно формулировать по разному.
Теорема может быть сформулирована в категорической форме и в условной форме.
Во всяком прямоугольнике диагонали равны.
Если четырехугольник является прямоугольником, то в нем диагонали равны
В чем плюсы и минусы этих формулировок теоремы? Категорическая формулировка – лаконична. Однако если теорема сформулирована в условной форме, то легче отделить условие от заключения. Итак, мы выяснили, что теорема имеет структуру:
А ⇒В – это данная (прямая) теорема
Все кладут сначала в рот
А потом едят компот.
Он всегда наоборот!
Он сначала ест компот
За компотом – бутерброд.
Все собрались в огород –
Он остался у ворот…
Все остались у ворот –
Он собрался в огород…
ОН ВСЕГДА НАОБОРОТ!
( А Барто «Мальчик наоборот»)
Если вданном предложенииА⇒В поменять условие и заключение местами, то получим
В ⇒А – обратноеутверждение (теорема)
Давайте немного поговорим об этом виде теорем.
Предложение «Если В то А » не всегда является теоремой.
« Если А то В ».«если четырехугольник является прямоугольником, то в нем диагонали равны».
«Если В то А ».«если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником»
Предложение, обратное истинному, может быть как истинным, так и ложным. Обратное предложение, истинность которого доказана, называется обратной теоремой.
Для любой теоремы вида А⇒ В (если А, то В) можно сформулировать предложение 
⇒ 
(если не А, то не В), которое называют противоположным данному.
А ⇒
В – противоположноеутверждение (теорема)
Предложение противоположное истинному может быть как истинным, так и ложным. В том случае, если предложение, противоположное данному, будет истинно, его называют теоремой, противоположной данной.
Для всякой теоремы видаА⇒В (еслиА, то В) можно сформулировать предложение 
(если не В, то не А), которое называют обратным противоположному.
- В ⇒
А–утверждение (теорема), обратное противоположному.Это, как известно, предложение истинное, и, следовательно, является теоремой, обратно противоположной данной.
Вообще, для какой бы теоремы мы ни формулировали предложение, обратное противоположному, оно всегда будет теоремой, потому что имеется следующая равносильность:
(А
В) 
(
).
Эту равносильность называют законом контрапозиции.
Из закона контрапозиции следует, что обратное (В⇒А) и противоположное (
⇒
) утверждения всегда имеют равное значение истинности.
(В⇒А)⇔(
⇒ 
)
Подведем итоги. О каких видах теорем мы узнали
А ⇒В – это данная (прямая) теорема
В ⇒А – обратное утверждение (теорема)
А ⇒ В – противоположное утверждение (теорема)
В ⇒ А – утверждение (теорема), обратное противоположному
( А⇒ В) ⇔ (В⇒ А ) – закон контрапозиции (В ⇒А) ⇔ ( А ⇒ В)
Использование теорем в начальном курсе математики
В учебниках математики для начальных классов не встречаются теоремы, но много предложений, называемых правилами и формулами. Их получают, упрощая теоремы, опуская все условия, указанные в теореме. Это позволяет быстрее запоминать правила и формулы.
Например, правило деления суммы на число «для того, чтобы разделить сумму на число, можно разделить на это число каждое из слагаемых и полученные результаты сложить». К этой формулировке дана формула: (a + b):c = a:c + b:c.
Т. к. материал изучают в начальной школе, то надо понимать, что числа a, b и cмогут быть только целыми неотрицательными, причем с≠0. Кроме того правой частью можно воспользоваться при условии, что а кратно с и b кратно с.
Т. о. в основе правила деления суммы на число лежит теорема, которую можно сформулировать так: «Если a, b и c – целые неотрицательные числа (с≠0) иа кратно с и bкратно с, то разделить сумму a + b на число с можно, разделив на это число каждое из слагаемых».
Закрепление изученного материала (выполнение практической работы).
Примените полученные сегодня знанияна теоремах по схемам лежащим у вас на столах
Подведение итогов занятия. Рефлексия.
Домашнее задание. Слайд
П. 23 учебного пособия
карточка «Блиц-опрос» (студента ___________________________)
1. Определите значение истинности высказываний:
а) Число 6 делится на 2 и на 3.
б) Число 28 делится на 7 или на 9.
в) при делении 42 на 5 в остатке получится 2 или 5.
Запишите предложение математическими символами: Некоторые нечетные числа делятся на 5 ( 
Х – множество нечетных чисел Прочитайте следующие записи, заменив символы словесными выражениями: (
x2-1 = (x+1)(x-1)
Данные ниже высказывания взяты из учебника математики для начальных классов. Выясните, какие из них содержат квантор в явном или неявном виде:
а) От перестановки слагаемых сумма не изменяется;
б) Площадь прямоугольника равна произведению его длины на ширину;
в) Существуют четные числа;
г) Некоторые числа делятся на 4;
д) Среди многоугольников есть треугольники.
4. Постройте отрицания следующих высказываний и высказывательных форм:
Некоторые однозначные числа делятся на 10 При делении числа 32 на 5 в остатке получится 7 Число 123 делится на 9 3+2 4; Треугольник АВС – прямоугольный.