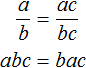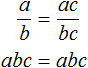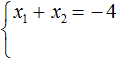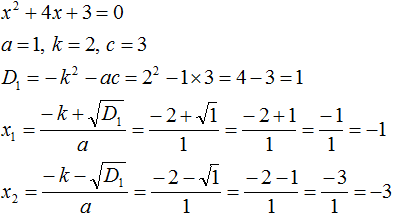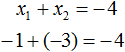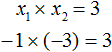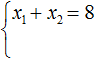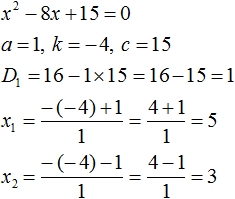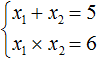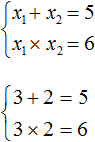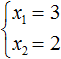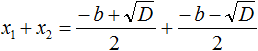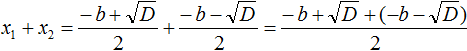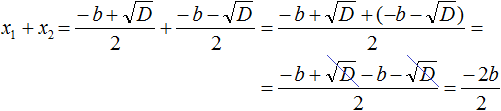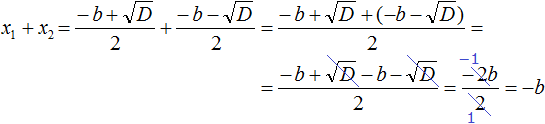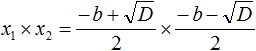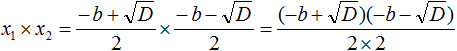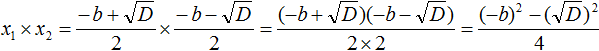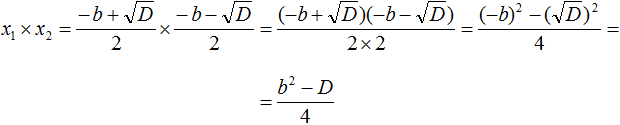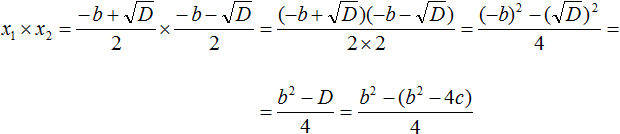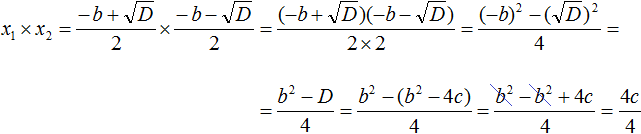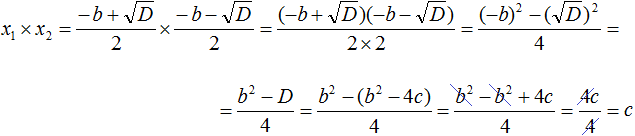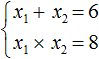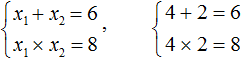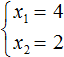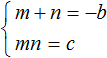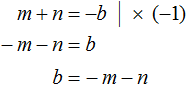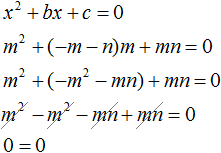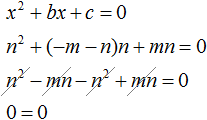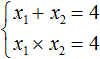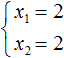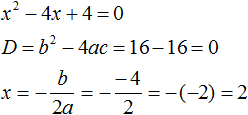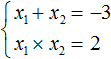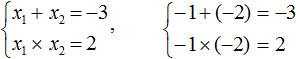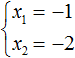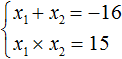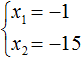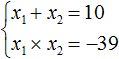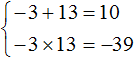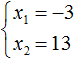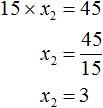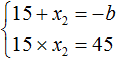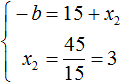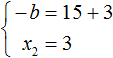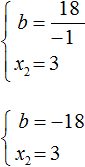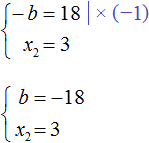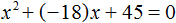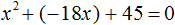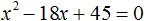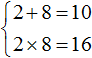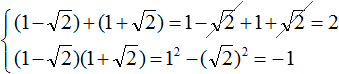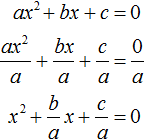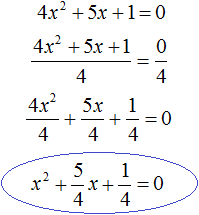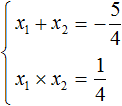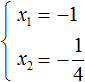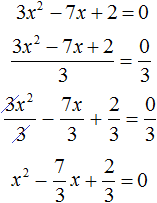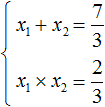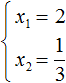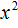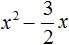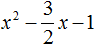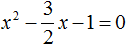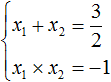теорема виета когда нельзя применять
Теорема виета когда нельзя применять
Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте III Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://www.school-science.ru/0317/7/28946.
Объекты проекта: целые рациональные уравнения и многочлены различных степеней.
Предмет проекта: теорема Виета как инструмент для решения уравнений и вычисления значений многочленов различных степеней.
Цель работы: создание электронного пособия, которое может быть использовано как при классно – урочной, так при дистанционной системе обучения, расширит знания и возможности учащихся по данной теме за пределы страниц школьного учебника, путём обобщения теоремы Виета для уравнений высших степеней и применения специальных методов решения задач.
Задачи:
1. На примере биографии великого ученого показать движущие силы научной мысли.
2. Сформулировать, доказать и научить использовать теорему Виета в стандартных математических задачах.
3. Исследовать возможность обобщения теоремы для уравнений высших степеней.
4. Рассмотреть нестандартные методы решения математических задач, используя теорему Виета.
5. Экспериментально убедиться в рациональности применения теоремы.
6. Предложить материалы проверки как для теоретической, так и для практической подготовленности учащихся.
7. Вызвать активный познавательный интерес, который позволит глубже изучить проблему.
Теорема Франсуа Виета и её значение в математике
Франсуа Виет – выдающийся французский математик XVI в., положивший начало алгебре как науке. По образованию и основной профессии – юрист, по склонности души – математик.Франсуа Виет родился в 1540 г. на юге Франции в небольшом городке Фантене-ле-Конт, что находится в 60 км от Ла Рошели, бывшей в то время оплотом французских протестантов-гугенотов. Большую часть жизни он прожил рядом с виднейшими руководителями этого движения, хотя сам оставался католиком. Отец Виета был юристом, а мать (Маргарита Дюпон) происходила из знатной семьи, что облегчило дальнейшую карьеру её сына.По традиции сын выбрал профессию отца и стал юристом, окончив университет в Пуату. В 1560 году двадцатилетний адвокат начал свою карьеру в родном городе, но через три года перешел на службу в знатную гугенотскую семью де Партене. Он стал секретарем хозяина дома и учителем его дочери двенадцатилетней Екатерины. Именно преподавание пробудило в молодом юристе интерес к математике.Когда ученица выросла и вышла замуж, Виет не расстался с ее семьей, а переехал с нею в Париж, где ему было легче узнать о достижениях ведущих математиков Европы.
Жизненный путь. На государственной службе
В 1571 году Виет перешел на государственную службу, став советником парламента, а затем советником короля Франции Генриха III.В ночь на 24 августа 1572 года в Париже произошла массовая резня гугенотов католиками, так называемая Варфоломеевская ночь. В ту ночь вместе со многими гугенотами погибли муж Екатерины де Партене и математик Рамус. Во Франции началась гражданская война.
Через несколько лет Екатерина де Партене снова вышла замуж. На сей раз, ее избранником стал один из видных руководителей гугенотов – принц де Роган. По его ходатайству в 1580 году Генрих III назначил Виета на важный государственный пост рекетмейстера, который давал право контролировать от имени короля выполнение распоряжений в стране и приостанавливать приказы крупных феодалов.
Находясь на государственной службе, Виет оставался ученым. К этому времени относятся свидетельства современников Виета о его огромной трудоспособности. В 1584 году по настоянию Гизов Виета отстранили от должности и выслали из Парижа. Именно на этот период приходится пик его творчества. Обретя неожиданный покой и отдых, ученый поставил своей целью создание всеобъемлющей математики, позволяющей решать любые задачи… И он справился со своей задачей…
Интересные факты из жизни и деятельности ученого
Франсуа Виет, вычисляя периметры вписанного и описанного 322 216–угольников, получил 9 точных десятичных знаков.
Впервые обозначать десятичные дроби с помощью запятой предложил Франсуа Виет. До него изображение дробей было весьма сложным. Так, например, дробь 0,3469 писалась так: 3(1)4(2)6(3)9(4).
Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым он внедрил в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т.е. ввести понятие математической формулы.
Франсуа Виет, вычисляя периметры вписанного и описанного 322 216–угольников, получил 9 точных десятичных знаков.
Впервые обозначать десятичные дроби с помощью запятой предложил Франсуа Виет. До него изображение дробей было весьма сложным. Так, например, дробь 0,3469 писалась так: 3(1)4(2)6(3)9(4).
Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым он внедрил в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т.е. ввести понятие математической формулы
Ученый мог работать по трое суток без сна!
Теорему Виета можно обобщить на многочлены любой степени.
Непосредственно применение трудов Виета очень затруднялось тяжелым и громоздким изложением. Из-за этого они полностью не изданы до сих пор.
Г.Г. Цейтен отмечал, что чтение работ Виета затрудняется несколько изысканной формой, в которой повсюду сквозит его большая эрудиция, и большим количеством изобретенных им и совершенно не привившихся греческих терминов. Потому влияние его, столь значительное по отношению ко всей последующей математике, распространялось сравнительно медленно.
Виет первым стал применять скобки, которые, правда, у него имели вид не скобок, а черты над многочленом.
Главные открытия Ф. Виета изложены в знаменитом «Введении в аналитическое искусство», опубликованном в 1591 году. Основной замысел ученого замечательно удался: началось преобразование алгебры в мощное математическое исчисление. Франсуа называл алгебру аналитическим искусством. Он писал в письме к де Партене: «Все математики знали, что под алгеброй скрыты несравненные сокровища, но не умели их найти…»
Теорема: Знаменитая теорема, устанавливающая связь коэффициентов многочлена с его корнями, была обнародована в 1591 году. Теперь она носит имя Виета, а сам автор формулировал ее так:
«Если В+D, умноженное на А, минус А в квадрате равно ВD, то А равно В и равно D».
Это выражение можно переписать в привычном для нас виде:
Во время затяжной войны между Францией и Испанией, испанские инквизиторы, воюя против протестантской церкви, использовали шпионскую связь. Они считали, что придуманный ими шифр для шпионских донесений, состоящий из 600 знаков не доступен для разгадывания. Но вдруг инквизиторы узнали, что шифр расшифрован и в этом причина их неудач. Разгадал тайну шифра Франсуа Виет. Испанские инквизиторы заявили о том, что простой человек не мог разгадать шифр, обвинили Виета в заговоре с нечистой силой, которая якобы помогла ему. Заочно Виет был приговорен к смерти. Возможно, что приговор и был со временем исполнен.
Теорема Виета для квадратного уравнения
Основные понятия
Квадратное уравнение — это ax 2 + bx + c = 0, где a — первый коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Существует три вида квадратных уравнений:
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Формула для его поиска записывается так: D = b 2 − 4ac. Его свойства:
В математике теоремой принято называть утверждение, у которого ранее было сформулировано доказательство.
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Доказательство теоремы Виета
Дано квадратное уравнение x 2 + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:
Докажем, что следующие равенства верны
Чтобы найти сумму корней x₁ и x₂ подставим вместо них то, что соответствует им из правой части формул корней. Напомним, что в данном квадратном уравнении x 2 + bx + c = 0 старший коэффициент равен единице. Значит после подстановки знаменатель будет равен 2.
Мы доказали: x₁ + x₂ = −b.
Далее произведем аналогичные действия, чтобы доказать о равенстве x₁ * x₂ свободному члену c.
Мы доказали: x₁ * x₂ = c.
Значит сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком (x₁ + x₂ = −b), а произведение корней равно свободному члену (x₁ * x₂= c). Теорема доказана.
Обратная теорема Виета
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Она формулируется так:
Обратная теорема Виета
Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x 2 + bx + c = 0.
Обратные теоремы зачастую сформулированы так, что их утверждением является заключение первой теоремы. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это является утверждением.
Докажем теорему, обратную теореме Виета
Корни x₁ и x₂ обозначим как m и n. Тогда утверждение будет звучать следующим образом: если сумма чисел m и n равна второму коэффициенту x 2 + bx + c = 0, взятому с противоположным знаком, а произведение равно свободному члену, то числа m и n являются корнями x 2 + bx + c = 0.
Зафиксируем, что сумма m и n равна −b, а произведение равно c.
Чтобы доказать, что числа m и n являются корнями уравнения, нужно поочередно подставить буквы m и n вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями x 2 + bx + c = 0.
При x = m получается верное равенство. Значит число m является искомым корнем.
Мы доказали: числа m и n являются корнями уравнения x 2 + bx + c = 0.
Примеры
Для закрепления знаний рассмотрим примеры решения уравнений по теореме, обратной теореме Виета.
Дано: x 2 − 6x + 8 = 0.
Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2 − 6x + 8 = 0″ height=»59″ src=»https://lh6.googleusercontent.com/tFokx3SM93Hwlr7ZM9BqX1xiHKv_2dUIB9MoNa8RAwSTmQKXdCcqcFXxTZmxNGw7bOVek-RzRXqBkoCqnYMiqIYVwKhfnHeU-7mA03feEqJTlyKB7e-OsTTKgPaOlddfiaTGszcv» width=»99″>
Имея эти два равенства можно подобрать подходящие корни, которые будут удовлетворять как равенству обоим равенствам системы.
Подбор корней удобнее выполнять с помощью их произведения. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. Значения 4 и 2 подходят обоим равенствам:
Значит числа 4 и 2 являются корнями уравнения x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»57″ src=»https://lh3.googleusercontent.com/rohB7Bvd-elMhTxEUuOhKqLJjqLAvo9VlJxZvOnMeDAHARfKT-SYOWb1WXTTWEN2h0oKbLl6wH7lc0IWL_vH3Si2AJGAGXVn8TPFDT_J1Wu2WeoQ-WP1qgXjCnZ99tWUkK2BOvF2″ width=»64″>
Неприведенное квадратное уравнение
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым, то есть его первый коэффициент равен единице:
ax 2 + bx + c = 0, где а = 1.
Теорема Виета
После того, как вы внимательно изучите, как решать квадратные уравнения обычным образом с помощью формулы для корней можно рассмотреть другой способ решения квадратных уравнений — с помощью теоремы Виета.
Перед тем, как изучить теорему Виета, хорошо потренируйтесь в определении коэффициентов « a », « b » и « с » в квадратных уравнениях. Без этого вам будет трудно применить теорему Виета.
Когда можно применить теорему Виета
Не ко всем квадратным уравнениям имеет смысл использовать эту теорему. Применять теорему Виета имеет смысл только к приведённым квадратным уравнениям.
Приведенное квадратное уравнение — это уравнение, в котором старший коэффициент « a = 1 ». В общем виде приведенное квадратное уравнение выглядит следующим образом:
Обратите внимание, что разница с обычным общим видом квадратного уравнения « ax 2 + bx + c = 0 » в том, что в приведённом уравнении « x 2 + px + q = 0 » коэффициент « а = 1 ».
Если сравнить приведенное квадратное уравнение « x 2 + px + q = 0 » с обычным общим видом квадратного уравнения « ax 2 + bx + c = 0 », то становится видно,
что « p = b », а « q = c ».
Теперь давайте на примерах разберем, к каким уравнениям можно применять теорему Виета, а где это не целесообразно.
Так как « a = 1 » можно использовать теорему Виета.
Приведем уравнение к общему виду:
Так как « a = 3 » не следует использовать теорему Виета.
Приведем уравнение к общему виду:
Так как « a = −1 » не следует использовать теорему Виета.
Как использовать теорему Виета
Теперь мы готовы перейти к самому методу Виета для решения квадратных уравнений.
Теорема Виета для приведённых квадратных уравнений « x 2 + px + q = 0 » гласит что справедливо следующее:
Чтобы было проще запомнить формулу Виета, следует запомнить:
«Коэффициент « p » — значит плохой, поэтому он берется со знаком минус ».
Так как в этом уравнении « a = 1 », квадратное уравнение считается приведённым, значит, можно использовать метод Виета. Выпишем коэффициенты « p » и « q ».
Запишем теорему Виета для квадратного уравнения.
| x1 + x2 = − 4 |
| x1 · x2 = −5 |
Методом подбора мы приходим к тому, что корни уравнения « x1 = −5 » и « x2 = 1 ». Запишем ответ.
Рассмотрим другой пример.
Старший коэффициент « a = 1 » поэтому можно применять теорему Виета.
| x1 + x2 = − 1 |
| x1 · x2 = −6 |
Методом подбора получим, что корни уравнения « x1 = −3 » и « x2 = 2 ». Запишем ответ.
Если у вас не получается решить уравнение с помощью теоремы Виета, не отчаивайтесь. Вы всегда можете решить любое квадратное уравнение, используя формулу для нахождения корней.
Деление уравнение на первый коэффициент
Рассмотрим уравнение, которое по заданию требуется решить, используя теорему Виета.
Сейчас в уравнении « a = 2 », поэтому перед тем, как использовать теорему Виета нужно сделать так, чтобы « a = 1 ».
Для этого достаточно разделить все уравнение на « 2 ». Таким образом, мы сделаем квадратное уравнение приведённым.
Теперь « a = 1 » и можно смело записывать формулу Виета и находить корни методом подбора.
| x1 + x2 = − (−8) |
| x1 · x2 = −9 |
| x1 + x2 = 8 |
| x1 · x2 = −9 |
Методом подбора получим, что корни уравнения « x1 = 9 » и « x2 = −1 ». Запишем ответ.
Бывают задачи, где требуется найти не только корни уравнения, но и коэффициенты самого уравнения. Например, как в такой задаче.
Корни « x1 » и « x2 » квадратного уравнения « x 2 + px + 3 = 0 » удовлетворяют условию « x2 = 3x1 ». Найти « p », « x1 », « x2 ».
Запишем теорему Виета для этого уравнения.
По условию дано, что « x2 = 3x1 ». Подставим это выражение в систему вместо « x2».
| x1 + 3x1 = −p |
| x1 · 3x1 = 3 |
| 4x1 = −p |
| 3x1 2 = 3 |(:3) |
| 4x1 + p = 0 |
| x1 2 = 1 |
| p = −4x1 |
| x1 2 = 1 |
Решим полученное квадратное уравнение « x1 2 = 1 » методом подбора и найдем « x1 ».
Мы получили два значения « x1 ». Для каждого из полученных значений найдем « p » и запишем все полученные результаты в ответ.
Теорема Виета в общем виде
В школьном курсе математики теорему Виета используют только для приведённых уравнений, где старший коэффициент « a = 1 », но, на самом деле, теорему Виета можно применить к любому квадратному уравнению.
В общем виде теорема Виета для квадратного уравнения выглядит так:
x1 + x2 =
| ||
x1 · x2 =
|
Убедимся в правильности этой теоремы на примере. Рассмотрим неприведённое квадратное уравнение.
Используем для него теорему Виета в общем виде.
x1 + x2 =
| ||
x1 · x2 =
|
| x1 + x2 = −1 |
| x1 · x2 = −6 |
Методом подбора получим, что корни уравнения « x1 = −3 » и « x2 = 2 ». Запишем ответ.
В заданиях школьной математики мы не рекомендуем использовать теорему Виета в общем виде.
Другими словами, реальную пользу теорема Виета приносит только для приведённых квадратных уравнений, в которых « a = 1 ». Именно в таких случаях она не усложняет жизнь, а позволят без дополнительных расчетов быстро найти корни.
Теорема Виета
Что называют теоремой?
Если человек обнаружил в математике какую-нибудь закономерность, позволяющую быстро решить ту или иную задачу, то ему не следует говорить о том, что он сделал открытие. Потому что может случиться так, что эта закономерность работает только для определённых случаев, а для других не работает или вовсе решает задачу неправильно.
Чтобы поделиться своим открытием с другими людьми, найденную закономерность следует сформулировать в виде утверждения, а затем доказать это утверждение, приводя неоспоримые факты.
Сформулированное утверждение называют теоремой. А доказательство теоремы состоит из фактов, логических рассуждений и вычислений, которые не оспариваются.
Например, теоремой можно назвать следующее утверждение:
«Если числитель и знаменатель обыкновенной дроби умнóжить на какое-нибудь число, то значение данной дроби не измéнится».
А затем привести такое доказательство:
Для доказательства этого равенства воспользуемся основным свойством пропорции:
От перестановки мест сомножителей произведение не меняется. Поэтому в получившемся равенстве можно упорядочить правую часть по алфавиту:
Поскольку равенство 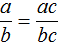

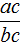
Теорема Виета
Французский математик Франсуа Виет выявил интересную взаимосвязь между коэффициентами приведённого квадратного уравнения и корнями этого же уравнения. Эта взаимосвязь представлена в виде теоремы и формулируется так:
Сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.
Знак системы (фигурная скобка) говорит о том, что значения x1 и x2 удовлетворяют обоим равенствам.
Значит выражение 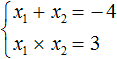
Значит выражение 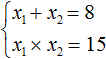
Замечание. Чтобы теорема Виета выполнялась, квадратное уравнение обязательно должно быть приведённым и иметь корни.
А значит записывать выражение 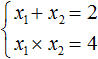
Теорема Виета полезна тем, что позволяет до начала решения узнать знаки корней уравнения.
Например, запишем для уравнения x 2 − 5x + 6 = 0 сумму и произведение его корней. Сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Доказательство теоремы Виета
Вспомним формулы корней квадратного уравнения:
Запишем правую часть в виде дроби с одним знаменателем:
Раскроем скобки в числителе и приведём подобные члены:
Подставим вместо x1 и x2 соответствующие выражения из формул корней квадратного уравнения. Не забываем, что коэффициент a всё ещё равен единице:
Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:
В получившемся выражении раскроем скобки в числителе и приведём подобные члены:
Сократим получившуюся дробь на 4
Таким образом, сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком ( x1 + x2 = −b ), а произведение корней равно свободному члену ( x1 × x2 = c ). Теорема доказана.
Теорема, обратная теореме Виета
Когда записана сумма и произведение корней приведённого квадратного уравнения, обычно начинается подбор подходящих корней к этому уравнению. В этот момент в работу включается так называемая теорема, обратная теореме Виета. Она формулируется так:
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел x1 и x2 равно свободному члену уравнения x 2 + bx + c = 0, то числа x1 и x2 являются корнями уравнения x 2 + bx + c = 0.
Обратные теоремы бывают поставлены так, что их утверждением является заключение первой теоремы.
Ранее мы решили уравнение x 2 − 5x + 6 = 0 и написали для него такую сумму и произведение корней:
Пример 2. Решить квадратное уравнение x 2 − 6x + 8 = 0 по теореме, обратной теореме Виета.
Число 8 можно получить если перемножить числа 4 и 2 либо 1 и 8.
Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x 2 + bx + c = 0, то числа m и n являются корнями уравнения x 2 + bx + c = 0
Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.
Примеры решения уравнений по теореме, обратной теореме Виета
Пример 1. Решить квадратное уравнение x 2 − 4x + 4 = 0 по теореме, обратной теореме Виета.
Запишем сумму корней x1 и x2 и приравняем её к второму коэффициенту, взятому с противоположным знаком. Также запишем произведение корней x1 и x2 и приравняем его к свободному члену :
Данный пример показывает, что теорема обратная теореме Виета, работает и для уравнений, имеющих только один корень. Признаком того, что квадратное уравнение имеет только один корень является то, что значения x1 и x2 совпадают.
Пример 2. Решить уравнение x 2 + 3x + 2 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Сумма бывает отрицательной если оба слагаемых отрицательны либо отрицательным является одно слагаемое, модуль которого больше.
Очевидно, что корнями являются два отрицательных числа. Произведение отрицательных чисел есть положительное число. А сумма отрицательных чисел есть отрицательное число.
Итак, корнями являются числа −1 и −2
Пример 3. Решить уравнение x 2 + 16x + 15 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Как и в прошлом примере сумма корней равна отрицательному числу, а произведение корней — положительному числу.
Произведение бывает положительным если оба сомножителя положительны либо оба сомножителя отрицательны. Первый вариант отпадает сразу, поскольку сумма корней равна отрицательному числу. Тогда получается, что оба корня будут отрицательными. Попробуем подобрать их.
Пример 4. Решить уравнение x 2 − 10x − 39 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Значит корнями уравнения x 2 − 10x − 39 = 0 являются числа −3 и 13
По теореме Виета произведение корней приведённого квадратного уравнения равно свободному члену. В данном случае это произведение равно 45
Этот второй корень также можно было бы получить, выразив из равенства 15 × x2 = 45 переменную x2
По теореме Виета сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней равна 18, а 18 это положительное число, то в самóм уравнении этот коэффициент будет отрицательным:
Обычно решение к такой задаче записывают так. Сначала записывают основную теорему Виета в виде суммы и произведения корней:
Из этой системы мы видим, что x2 равно 3. Подставим его в первое равенство:
Теперь из первого равенства мы видим, что −b равно 18
Этот же результат можно получить если в выражении 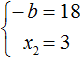
Теперь возвращаемся к исходному уравнению x 2 + bx + 45 = 0 и подставляем найденное значение b
Запишем сумму и произведение корней:
Пример 7. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 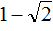
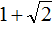
Запишем сумму и произведение корней:
Сумма корней равна 2. Тогда в уравнении второй коэффициент будет равен −2. А произведение корней равно −1. Значит свободный член будет равен −1. Тогда:
Когда квадратное уравнение неприведённое
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым.
Получилось уравнение 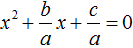


Получили приведённое квадратное уравнение. В нём второй коэффициент равен 

Отсюда методом подбора находим корни −1 и
Возможно этот метод вы редко будете использовать при решении квадратных уравнений. Но знать о нём не помешает.
Пример 2. Решить квадратное уравнение 3x 2 − 7x + 2 = 0
Данное уравнение не является приведённым, а значит его пока нельзя решить по теореме, обратной теореме Виета.
Сделаем данное уравнение приведенным. Разделим обе части на коэффициент, который располагается перед x 2
Получили уравнение 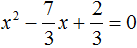
Отсюда методом подбора находим корни 2 и
Пример 3. Решить квадратное уравнение 2x 2 − 3x − 2 = 0
Прирáвниваем получившееся выражение к нулю:
Теперь применяем теорему Виета. Сумма корней будет равна второму коэффициенту, взятому с противоположным знáком, а произведение корней свободному члену:
Отсюда методом подбора находим корни 2 и