на ноль делить нельзя правило с примером
Почему делить на ноль нельзя?
Все математические действия равны, но некоторые равнее других
Начнём с того, что четыре арифметических действия — сложение, вычитание, умножение и деление — не являются равноправными. И разговор идёт не о порядке выполнения действий при решении какого-нибудь примера или уравнения. Нет, имеется в виду само понятие числа. И согласно ему, наиболее важными являются сложение и умножение. А уже вычитание и деление «вытекают» из них тем или иным образом.
Сложение и вычитание
Умножение и деление
Аналогичные метаморфозы происходят с таким действием, как деление. Задачу «6 : 3» математики отказываются воспринимать как некие шесть предметов, разбитых на три части. «Шесть разделить на три» не что иное, как «неизвестное число, умноженное на три, в результате чего получилось шесть»: «х · 3».
Делим на ноль
Выяснив принцип математических действий по отношению к задачам с вычитанием и делением, рассмотрим наше деление на ноль.
Задача «4 : 0» превращается в «х · 0». Получается, нам нужно найти такое число, умножение с которым даст нам 4. Известно, что умножение на ноль всегда даёт ноль. Это уникальное свойство нуля и, собственно, его суть. Числа, умноженного на ноль и выдающего любое другое число кроме нуля, не существует. Мы пришли к противоречию, значит задача не имеет решения. Следовательно, записи «4 : 0» не соответствует никакое определённое число, а отсюда уже вытекает её бессмысленность. Поэтому, чтобы кратко подчеркнуть непродуктивность такого процесса, как деление на ноль, и говорят, что «на ноль делить нельзя».
Больше интересных материалов:
А что получится, если ноль разделить на ноль?
Представим такое уравнение: «0 · x = 0». С одной стороны, выглядит вполне справедливо. Представляем вместо неизвестного числа ноль и получаем готовое решение: «0 · 0 = 0». Из этого вполне логично вывести, что «0 : 0 = 0».
Однако теперь давайте в это же уравнение с неизвестным вместо «x = 0» подставим любое другое число, например «x = 7». Получившееся выражение выглядит теперь как «0 · 7 = 0». Вроде бы, всё верно. Делаем обратную операцию и получаем «0 : 0 = 7». Но тогда, получается, что можно взять абсолютно любое число и вывести 0 : 0 = 1, 0 : 0 = 2. 0 : 0 = 145. — и так до бесконечности.
Если при любом числе х уравнение будет справедливо, то мы не имеем права выбрать лишь одно, исключив остальные. Значит, мы так и не можем ответить, какому числу соответствует выражение «0 : 0». Снова оказавшись в тупике, мы признаём, что и эта операция тоже бессмысленна. Получается, что ноль нельзя делить даже на самого себя.
Оговоримся, что в математическом анализе иногда бывают специальные условия задачи — так называемое «раскрытие неопределенности». В подобных случаях разрешается отдавать предпочтение одному из возможных решений уравнения «0 · x = 0». Однако в арифметике таких «допусков» не происходит.
Почему нельзя делить на ноль, даже если очень хочется?
Недавно на Хабре появилась удивительная статья «Папа, а почему на ноль делить нельзя?», которая собрала массу не менее удивительных комментариев.
Детские вопросы обычно очень сложны («Почему небо ночью темное?», «Почему яблоки падают на землю?») и у взрослых обычно не хватает времени, чтобы их доходчиво объяснить. Да и не всегда взрослые знают ответ на эти вопросы.
Однако, вопрос о делении на ноль ни разу не относится к числу сложных вопросов, и для меня остается загадкой, почему с ним возникает столько проблем. Наверное, виной тому какие-то изъяны в методике преподавания математики в средней школе, в трудностях перехода от изучения арифметики к изучению буквенной алгебры и свойств элементарных функций.
Самые серьезные сомнения появляются, я думаю, после изучения рациональных чисел, когда для любого числа x, кроме нуля, вводится понятие обратного числа 1/x, и графика гиперболы y(x)=1/x.
Очевидно, что при делении 1 на очень маленькие числа появляются очень большие числа, и чем меньше мы берем x, тем больше становится 1/x. Почему же мы не можем сказать, что 1/x=∞ — есть некоторое число?
Алгебраическое возражение против этого состоит в следующем. Предположим, что ∞=1/x является числом. Тогда на это число должны распространяться все правила, которые имеют место быть для обычных чисел. В частности, с одной стороны должно быть верно соотношение 0⋅∞=1, а с другой стороны поскольку 0=1−1 должно быть выполнено 0⋅∞=1⋅∞−1⋅∞=0. Таким образом, имеем 1=0, а из этого уже следует, что все числа равны между собой и равны нулю. В самом деле, поскольку для любого числа x верно 1⋅x=x, то 1⋅x=0⋅x=0.
«Ну разве это не полная чушь?» — спросим себя, добравшись до этого места.
Разумеется, это полная чушь, если мы говорим об обычных числах. Но я недаром подчеркнул выше слово «правила». К ним мы вернемся чуть позже, после рассмотрения арифметического возражения против деления на ноль, и поможет нам в этом фасоль.
Вернемся в те времена, когда не было ни компьютеров, ни калькуляторов, ни логарифмических линеек, и поставим перед собой задачу разделить некоторое случайное число, например, на 5.
Для этого берем чашу с фасолью, символизирующую натуральный ряд, и высыпаем из нее какое-то количество зерен на разлинованный лист бумаги:
Тем самым, мы установили делимое на нашем бобовом калькуляторе.
Задача состоит в том, чтобы разложить эти зерна на пять рядов. Чтобы не запутаться отмечаем эти ряды, то есть, устанавливаем делитель:
Теперь раскладываем зерна из кучи на пять рядов в столбик. Это значительно дольше, чем на обычном калькуляторе, зато позволяет почувствовать всю прелесть арифметики до изобретения позиционной системы счисления.
Алгоритм завершается, когда мы получаем некоторое прямоугольное число и (возможно) остаток:
В данном примере осталось 2 зерна, а рядов по 5 зерен образовалось 18. Получается, что случайное число было 18⋅5+2=92.
Ясно, что мы можем выполнить этот алгоритм для любого натурального делимого и любого натурального делителя, отличного от нуля; если же делитель равен 0, то этот алгоритм выполнить попросту невозможно.
«Подождите!» — скажет внимательный читатель. — «В рассмотренном примере мы получили остаток 2, что с ним делать?»
Это, на самом деле, очень важное замечание. Вообще говоря, мы не можем делить фасолины, не испортив наш бобовый калькулятор — мало того, что разделить 2 фасолины на 5 одинаковых частей проблематично, даже если мы их раздробим подобающим образом, мы уже не сможем их собрать.
Поэтому достаточно долго люди старались обходиться без дробей. Например, в анонимной арабской рукописи XII века описана следующая задача: «разделить 100 фунтов между 11 человеками». Поскольку 100=11⋅9+1, средневековый математик предлагает сначала раздать каждому по 9 фунтов, а затем обменять оставшийся фунт на яйца, которых, как оказывается по курсу обмена, получается ровно 91. Но 91=11⋅8+3, поэтому арабский ученый предлагает раздать каждому по 8 яиц, а три оставшихся яйца отдать тому, кто производит раздел, или же обменять на соль к яйцам.
Говоря современным математическим языком, деление проводилось в полукольце натуральных чисел. Впрочем, с таким же успехом, используя красную и белую фасоль, мы могли бы определить деление с остатком и в кольце целых чисел — в изложенном алгоритме появились бы дополнительные правила для выбора цветов используемых для вычислений зерен фасоли, но точно так же остались бы бессмысленными операции вида x/0 и 5/2.
Очевидно, что для того, чтобы придать символу 5/2 конкретный смысл, нужно изменить правила игры, и перейти к полю рациональных дробей, пополнив множество целых чисел всевозможными выражениями m/n, где m — целое, а n — натуральное.
Важно заметить, что сделать это можно не единственным способом, однако в классической арифметике рассматривается такое пополнение, в котором символ 1/n означает долю от деления 1 на n, т. е. такое число, для которого верно выражение n⋅1/n=1; при чем доли имеют смысл не при подсчете штучных предметов (например, зерен фасоли), а при измерении величин, которые предполагаются непрерывными (или хотя бы неограниченно делимыми) — длин отрезков, площадей фигур и т. д.
В поле рациональных дробей уже нет смысла рассматривать неполное частное и остатки, так как частное от любого ненулевого делителя является какой-то рациональной дробью. Более того, как и в случае с натуральными числами, мы можем использовать для деления фасоль без изменения алгоритма.
В самом деле, пусть требуется разделить рациональное число α=p/q на β=r/s. Это равносильно выполнению следующих действий:
и задача при любых рациональных α и β свелась к уже известной процедуре деления целых чисел. Это еще раз показывает, что деление на ноль не имеет никакого арифметического смысла.
«Получается, делить на ноль нельзя, даже если очень хочется?» — увы, ответ на этот вопрос положительный: мы не можем определить операцию деления на ноль исходя их естественных потребностей счета и измерений. Правда, есть две лазейки.
Первая: вместо «обычных» чисел (т.е. кольца натуральных и поля рациональных, а также поля действительных чисел, о котором я, кстати, до сих пор не сказал ни слова и расскажу как-нибудь в другой раз) рассмотреть вырожденный случай — тривиальное кольцо <0>, и положить по определению 0/0=0. В этом случае, когда нам говорят: «Все числа равны между собой и равны нулю!» — мы можем сказать невозмутимым тоном: «Ну и что? Это всегда было так».
Вторая: отказаться от некоторых привычных правил умножения. В частности, от аксиомы 0⋅x=0. Говорят, что это возможно (см. http://en.wikipedia.org/wiki/Wheel_theory). Разумеется, этот вариант гораздо интереснее первого, но и он представляет собой такое изменение правил игры, которое сразу выводит нас за рамки классической арифметики.
В заключение этой заметки хочу привести список литературы для тех, кто заинтересовался числовыми системами:
— И.В. Арнольд «Теоретическая арифметика», М, ОГИЗ 1938 — очень подробная и детальная книга, в которой можно найти описания классических числовых систем, включая кватернионы.
— Е. Г. Гонин «Теоретическая арифметика», М, 1959 — эта книга покороче и посовременнее, и тоже очень хороша, хотя не так подробна, как книга И.В. Арнольда.
— С. Феферман «Числовые системы» — классическая монография, местами достаточно сложная; в ней изложены некоторые частные вопросы, которых нет в двух других книгах по теоретической арифметике.
— А. А. Кириллов «Что такое число?» (1993) — небольшая брошюра, рассчитанная на подготовленного читателя.
— Е. Б. Дынкин, В. А. Успенский «Математические беседы» — популярная книга, рассчитанная на школьников. Содержит массу информации и задач по такой «нестандартной» теме, как p-адические числа.
Почему нельзя делить на ноль: простые объяснения
Вопросы школьников: Freepick
Почему нельзя делить на ноль? Кто и почему запрещает нам эту математическую операцию? Сразу отметим, что деление на ноль в рамках школьной программы определяется как операция, которую запрещено совершать, а вот высшая математика смотрит на этот вопрос иначе. Тем не менее школьники обязательно зададут вопрос, почему на ноль делить нельзя. Прочтите статью и будьте готовы простыми словами объяснить сложное явление.
Что будет, если разделить на ноль: индийский ответ
Ноль был придуман в Индии, равно как и отрицательные числа. Европейцам такие понятия даже в голову не приходили. А вот индийские философы любили задуматься о бесконечном «ничто» или о математическом выражении долгов. Так и возникла дилемма: делить на ноль или нет. Есть простые объяснения этого вопроса.
Почему нельзя делить на ноль: ответы: Nur.kz
Около 1400 лет назад в Индии жил и работал некто Брахмагупта, который не только сформулировал этот вопрос, но и нашел оригинальное объяснение. Логика ученого была такова:
Если при делении лимона получается не две части, а число, которое стремится к бесконечности, то каков будет размер каждой дольки? Наверное, столкнемся с бесконечным числом «нулевых долек». В реальной жизни результат такой нарезки — лужица лимонного сока с бессчетным количеством ломтиков.
То есть если число делить на бесконечность, то получится ноль и наоборот.
На ноль делить нельзя: нелогично
Рассмотрим простой пример:
Таким образом, любое число оказывается равным любому числу, а это невозможно.
Делением называют действие, обратное по отношению к умножению. Это означает, что при делении 6 на 3 необходимо отыскать число, которое в случае умножения на 3 даст 6.
Следуя этой логике, при делении 6 на 0, нужно выбрать число, умножение на 0 которого даст 6. То есть а × 0 = 6? Но а × 0 = 0! Снова неувязка. Сколько нам необходимо нолей, чтобы вышло 6? Неужели бесконечно много? Но и сложение такого количества нолей даст только ноль.
Отсюда и еще один вывод о том, что если ноль делить на ноль, выйдет неопределенный итог. В уравнении 0 × а = 0 в качестве составляющей «а» может оказаться все что угодно. В бесчисленном множестве решений смысла нет.
Можно ли делить ноль: жизненное объяснение
Представьте, что необходимо подсчитать время, за которое пройдете 10 километров. Известно уравнение, в котором для поиска длины пути скорость умножают на время. Чтобы найти время в нашем случае, будем путь делить на показатель скорости. Но что если наша скорость нулевая?
Мы не двигаемся, поэтому идти заветных 10 км нам предстоит вечность. Время при таких условиях попросту перейдет в бесконечную величину, которую подсчитать не выйдет.
Делить на ноль можно, но бессмысленно
Алгебра и деление на ноль: Freepick
Что собой представляет деление в алгебре:
Давайте проделаем ту же операцию с вещами. Например: если разложить 10 яблок по 2 штуки в коробки, то сколько необходимо коробок? Ответ — 5 коробок. Но в случае, если раскладывать 10 яблок по ноль единиц в коробки, то сколько коробок понадобится? Получается, что в коробках необходимости попросту нет, потому что класть в них нечего.
Деление на ноль: самое простое объяснение
Посчитаем: 12 : 2 = 6, 12 : 4 = 3. Чем больше число знаменателя, тем меньше получается результат. Наоборот это правило тоже работает: для маленьких чисел результат больше: 12 : 1,5 = 8, 12 : 1 = 12.
Что получится с очень малыми числами? Например, с 0,0000001 выйдет 100000000. При уменьшении знаменателя до нуля число должно получиться огромнейшее, а точнее — бесконечность.
Таким образом, на ноль делить нельзя из-за отсутствия материального выражения бесконечности. Итог такого действия смысла не имеет. Что касается высшей математики, то, кроме ноля, она оперирует также понятием о бесконечно малом и расширяет привычные горизонты вычислений.
Итак, почему нельзя делить на ноль? В рамках алгебры такая операция не определенная, не логичная и абстрактная. Если хотите детальнее разобраться в этом вопросе, то придется прибегнуть к высшей математике. Чтобы разобраться с позиции этой дисциплины с указанным алгебраическим правилом, нужно познакомиться с дельта-функцией Дирака и прочими сложными понятиями.
А как думаете вы, почему нельзя делить на ноль?
Узнавайте обо всем первыми
Подпишитесь и узнавайте о свежих новостях Казахстана, фото, видео и других эксклюзивах.
Учителя многое недоговаривали
Сразу же стоит отметить, что эта аксиома является не совсем правдивой. На самом деле на ноль делить можно, и конец света от этого не настанет. Просто уравнение будет иметь бесконечное количество решений. Чем-то напоминает число «Пи», которое можно высчитывать в течение всей жизни и так и не получить конечного результата. Однако когда человек учится в школе, у него даже не возникает вопроса о том, что будет, если поделить на ноль. Слова преподавателя он воспринимает на веру.
Но может ли учитель объяснить маленькому ребенку, что такое принцип неопределенности или натуральный предел? Куда проще будет сказать, что на 0 делить нельзя. Правило не является совсем правдивым, зато школьник не будет пытаться решить уравнение, которое имеет несколько миллиардов решений. Если же в процессе разбора задачи выходит так, что все-таки приходится поделить на ноль, значит, где-то была допущена ошибка.
На самом деле у такой задачи может быть и иное решение — бесконечность (при условии, что при расчетах не было допущено ошибок). Чтобы это доказать, не придется использовать формулу массы или закон сохранения энергии из физики. В
большинстве случаев алгебраическое доказательство сводится к решению одного простого уравнения или функции, которая в итоге имеет бесконечное количество решений.
Четыре действия в арифметике
Сложение, умножение, деление и вычитание — эти принципы известны каждому школьнику, учащемуся в средних классах. Однако далеко не все знают, что равноправными действиями обладают лишь первые два из них.
Деление и вычитание — это операции, которые являются обратными сложению и умножению. Любые действия в математике могут быть легко построены лишь с помощью этих двух основ. Нужно лишь знать, как правильно выражать деление с помощью умножения или вычитание с помощью сложения. Здесь на помощь приходят уравнения, а также положительные и отрицательные числа. Иногда также приходится возводить число в какую-нибудь степень.
Чтобы было более понятно, следует немного попрактиковаться в арифметике. Что значит пример: «4−2»? Большинство школьников ответит на него достаточно просто: «Нужно взять 4 предмета, после чего провести удаление — отнять два из них, а затем взглянуть, сколько осталось». Вот только профессиональные математики представляют эту задачу совершенно иначе. Ее решение будет представлено уравнением: «x+2=4», корень которого представлен заменой арифметического действия. Нетрудно догадаться, что число «x» будет равно двум. Стоит отметить, что пример был решен без единого минуса.
Теперь немного о том, почему деление не считается полноправным действием в арифметике. В качестве примера возьмем следующее уравнение: «8:4=x». Всем и так понятно, что число «x» будет равно двум. Однако как получить это значение, не используя при этом деление? Правильно, нужно заменить его умножением. В результате математик получит уравнение: «x*4=8». Все очень просто и логично. Однако именно благодаря тому, что мы можем разделить, просто умножив, появляется первое определение того, что деление на ноль не имеет никакого смысла.
Попробуем решить простой пример: «6:0». Пятиклассник сразу скажет, что оно не имеет решения. Однако мы ведь знаем, что можно записать это же выражение другой фразой: «0*x=6». То есть математик получает задание отыскать число, которое бы при умножении на 0 дало ему 6. Вот только каждому известно, что при умножении на 0 в итоге все равно получится 0. Это свойство числа является неотъемлемым и любой шанс опровергнуть аксиому лишен всякого смысла. Именно поэтому учителя и будут продолжать запрещать ученикам делить на ноль, ведь решить уравнение с умножением на это число попросту невозможно.
Принцип бесконечности
Однако деление на ноль в высшей математике все-таки имеет решение. И оно даже не одно, их огромное множество. Этот прием называется принципом бесконечности и доказывает, что все-таки существует одно единственное число, которое можно разделить на ноль. Какое именно? Ну конечно же, сам ноль! Ведь если мы возьмем уравнение: «0*x=0», то оно будет успешно решаться — x будет равен нулю или любому другому числу, например, 512.
В этом и заключается принцип бесконечности. Ведь если вместо неизвестного показателя можно поставить любое число, то это значит, что уравнение с делением имеет огромное количество решений. Самое главное, чтобы один из множителей в обратном уравнении был также равен нулю. Другими словами, этот математический феномен также называется «принципом неопределенности» — какое бы число вы ни подставили вместо «x» (с плюсом или минусом, целое или дробное — неважно) — операция будет иметь неопределенное количество решений.
Работает ли этот факт с вычитанием? Не совсем! Если вы возьмете 5 яблок и вычтете из них ноль, то в итоге получится число, равное пяти. Но что если мы заменим одно из слагаемых числом «x»? Получится уравнение «5+x=5» Нетрудно догадаться, что уравнение имеет только одно решение, которое равно нулю. Однако можно ли подставить еще какое-то число, которое при сложении с другим отразит его зеркально? Разумеется, нет.
В этом и заключается одна из главных особенностей нуля. Если вы видите уравнение, в котором присутствует два слагаемых, а сумма равняется 5, то можете смело писать в решении «0», даже если вместо x там написана сложная система или логарифм.
Арифметическая шутка с нулем
Правило «делить на ноль нельзя» (пример в предыдущем разделе) лежит в основе многих арифметических шуток, которые могут доказывать, что 2+2 равняется не 4, а 7. Однако если математик уяснит его, то никогда не будет введен в заблуждение. Возьмем в качестве примера уравнение «4*x+2-=7*x-35.» Подробный алгоритм решения выглядит следующим образом:
Однако весь подвох заключается в том, что корень уравнения был равен пяти, а сокращать его с помощью дроби было нельзя, поскольку в итоге это привело к тому, что все уравнение было поделено на ноль. Поэтому при решении таких задач следует помнить важное правило: нельзя допускать, чтобы в знаменателе дроби оказался ноль. В противном случае это приведет вот к такому забавному решению, которое натолкнет математика на «открытие» ранее неизведанных «теорем».
Философия, да и только
Многие люди используют пример с делением на ноль для того, чтобы объяснить некоторые закономерности, которые попросту не поддаются объяснению. Ведь что представляет собой само понятие «бесконечность», которую мы иногда можем получить в процессе решения некоторых уравнений? Никто не сможет ответить на этот вопрос, поскольку он находится за пределами нашего понимания. Это как объяснять гусенице, что такое закон притяжения. Безусловно, он на нее действует, однако столь примитивный организм никогда не сможет понять те законы, которые нас окружают, ведь ей движут всего лишь инстинкты.
То же самое и с делением на бесконечность. Да, мы можем записать огромное количество решений для функций и уравнений, в которых приходится делить на ноль. Но что в итоге это даст? Бесконечность — число или понятие, которое находится за гранью нашего восприятия. Решение подобного уравнения сравнимо с путешествием в кроличью нору. Даже если конечный результат не будет достигнут — есть над чем задуматься. К примеру, насколько же все-таки многогранным и удивительным является это число — ноль. Оно одновременно ничего не значит и значит слишком много.
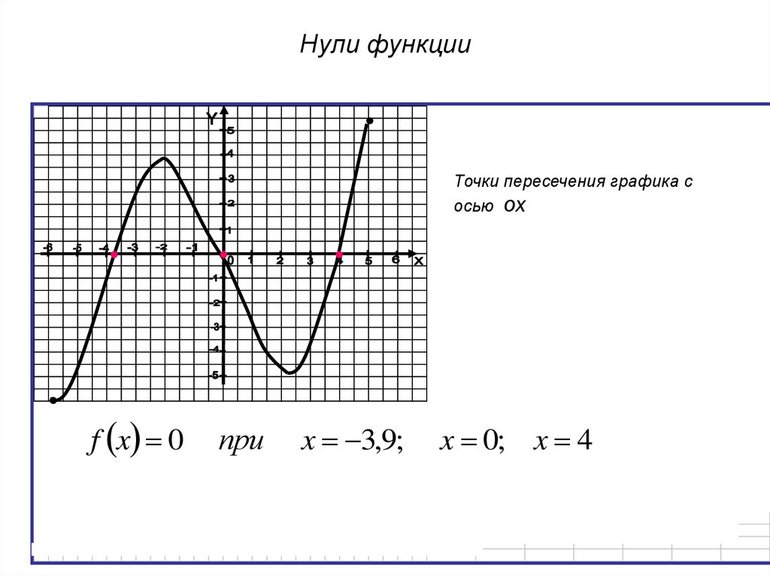
График функции с нулем
Лучше всего понять, что тип уравнения, в котором приходится делить на ноль, имеет бесконечное количество решений, помогает обычный график функции, который доводилось изучать каждому школьнику. Если говорить точнее, то потребуется гипербола, которая имеет обратную зависимость от функции. Выглядит рисунок в виде кривой с асимптотами — прямыми линиями, к которым симметрично стремится гипербола. Однако всем известно, что она никогда их не достигнет. Да, она пересекается возле точки, которая максимально близка к нулю, однако все-таки не достигает ее.
Вот такая получается математическая драма. Чем ближе функция приближается к своему значению, тем больше становится показатель «игрек», а «икс» — уменьшается. То есть если «y» будет стремиться к нулю, то «x» станет стремиться к бесконечности (или минус бесконечности). Так что такая функция не будет иметь решений, как бы математик не старался. Но ведь, по сути, в процессе решения никто не делит число на ноль. В роли делителя выступает число, которое имеет ничтожно малую величину. Вот так.
Именно поэтому многие опытные математики говорят, что при делении на ноль мы получаем бесконечность со знаком плюс или минус (в зависимости от знаменателя). Само собой, можно расписать на бумаге огромное множество решений до тех пор, пока известные числа просто не закончатся. Но стоит ли тратить свою жизнь на то, чтобы делать это? Ведь даже в школе учеников держат подальше от того, чтобы связываться с делением на ноль. Решить такое уравнение попросту невозможно, поскольку существуют миллиарды и даже триллионы возможных решений. Вот такой забавный парадокс с этим нулем.
Несколько умных ответов математикам
Поскольку решить уравнение с делением на ноль невозможно, стоит рассмотреть вариант ответов на случай, если на экзамене или где-нибудь на собеседовании будет задан вопрос от математика: «Почему на ноль делить нельзя?» Вот лишь несколько вариантов ответов, которые можно использовать и не ошибиться:
Ну а в качестве примера или «доказательства» аксиомы можно использовать уравнения, которые являются обратными общепринятым арифметическим действиям. Вот лишь несколько из них:
Многие работодатели и авторитетные личности, которые хотят проверить человека с математическим образованием на его знания, попросят доказать принцип бесконечности, на что можно привести эти простые примеры. Ведь каждый высший математик должен не просто знать правило, что на ноль делить нельзя, а уметь объяснить, почему именно решение таких уравнений является бессмысленным.
Надеемся, теперь вы понимаете, что решение задач, в которых в качестве делителя выступает ноль, неприлично много. Это значит, что пытаться разобрать их будет бессмысленно, поскольку принцип неопределенности попросту не даст довести пример до логического завершения.
Возможно, именно поэтому индейцы племени Майя и называли это число «началом и бесконечностью», ведь даже график функции никогда его не достигнет.