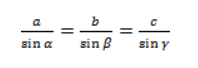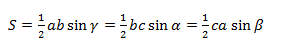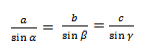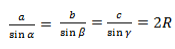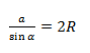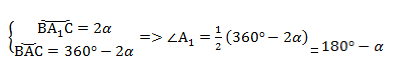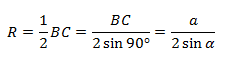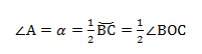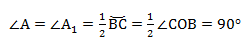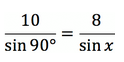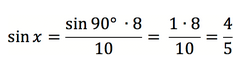когда вокруг треугольника можно описать окружность
Окружность, описанная около треугольника
Что такое окружность, описанная около треугольника? Что является центром этой окружности? Как расположение центра описанной окружности зависит от вида треугольника?
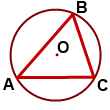
Окружность называется описанной около треугольника, если все вершины треугольника лежат на окружности.
Расстояние от любой вершины треугольника до центра описанной окружности равно радиусу этой окружности.
Окружность можно описать около любого треугольника.
Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника (то есть отрезков, перпендикулярных к сторонам треугольника и проходящих через середины этих сторон).
Центр окружности, описанной около остроугольного треугольника, лежит внутри треугольника.
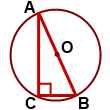
Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.
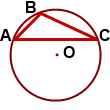
Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника (напротив тупого угла, за большей стороной).
Описанная окружность (ЕГЭ 2022)
Первый вопрос, который может возникнуть: описанная – вокруг чего?
Ну, вообще-то иногда бывает и вокруг чего угодно, а мы будем рассуждать об окружности, описанной вокруг (иногда ещё говорят «около») треугольника.
Описанная окружность — коротко о главном
Определение
Окружность, описанная около треугольника – это окружность, которая проходит через все три вершины этого треугольника.
Центр описанной окружности
Вокруг всякого треугольника можно описать окружность, при том единственным образом.
Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.
Радиус описанной окружности
Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, нужна одна сторона (любая!) и противолежащий ей угол.
Расположение центра описанной окружности
В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника
В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.
Описанная окружность — подробнее
Определение
Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана.
Свойства и центр описанной кружности
И вот, представь себе, имеет место удивительный факт:
Вокруг всякого треугольника можно описать окружность.
Почему этот факт удивительный?
Потому что треугольники ведь бывают разные!
И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.
Доказательство этого удивительного факта мы приведем чуть позже, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины.
Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!
А есть только для прямоугольника:
Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.
Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника.
Знаешь ли ты, что такое серединный перпендикуляр?
Серединный перпендикуляр — это прямая, проходящая через середину отрезка и перпендикулярная ему.
Прямая \( \displaystyle a\) – это серединный перпендикуляр к отрезку \( \displaystyle AB\).
А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.
Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), что все три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке \( \displaystyle O\).
Это и есть центр описанной около (вокруг) треугольника \( \displaystyle ABC\) окружности.
Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!
Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!
А вот если остроугольный, то внутри:
Что же делать с прямоугольным треугольником?
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов!
Да ещё с дополнительным бонусом:
В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.
Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.
В произвольном треугольнике:
\( \Large \displaystyle \frac<\sin \angle A>=2R\)
То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол.
Хорошая формула? По-моему, просто отличная!
Доказательство теоремы
Теорема. Вокруг всякого треугольника можно описать окружность, при том единственным образом.
Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.
Давай наберёмся мужества и докажем эту теорему.
Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.
Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).
Геометрическое место точек, обладающих свойством «\( \displaystyle X\)» — такое множество точек, что все они обладают свойством «\( \displaystyle X\)» и никакие другие точки этим свойством не обладают.
Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы.
А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют.
В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:
Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка.
Тут множество – это серединный перпендикуляр, а свойство «\( \displaystyle X\)» — это «быть равноудаленной (точкой) от концов отрезка».
Проверим? Итак, нужно удостовериться в двух вещах:
Проверим 1. Пусть точка \( \displaystyle M\) лежит на серединном перпендикуляре к отрезку \( \displaystyle AB\).
Соединим \( \displaystyle M\) с \( \displaystyle A\) и с \( \displaystyle B\).Тогда линия \( \displaystyle MK\) является медианой и высотой в \( \displaystyle \Delta AMB\).
Значит, \( \displaystyle \Delta AMB\) – равнобедренный, \( \displaystyle MA=MB\) – убедились, что любая точка \( \displaystyle M\), лежащая на серединном перпендикуляре, одинаково удалена от точек \( \displaystyle A\) и \( \displaystyle B\).
Теперь 2. Почти точно так же, но в другую сторону. Пусть точка \( \displaystyle M\) равноудалена от точек \( \displaystyle A\) и \( \displaystyle B\), то есть \( \displaystyle MA=MB\).
Возьмём \( \displaystyle K\) – середину \( \displaystyle AB\) и соединим \( \displaystyle M\) и \( \displaystyle K\). Получилась медиана \( \displaystyle MK\). Но \( \displaystyle \Delta AMB\) – равнобедренный по условию \( \displaystyle (MA=MB)\Rightarrow MK\) не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка \( \displaystyle M\) — точно лежит на серединном перпендикуляре.
Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.
Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».
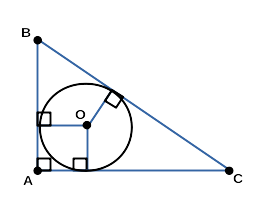
Треугольник описанный около окружности
Определение
Треугольник, описанный около окружности — это треугольник,
который находится около окружности и соприкасается
с ней всеми тремя сторонами.
На рисунке ниже изображена окружность, вписанная в треугольник;
и треугольник, описанный около окружности.
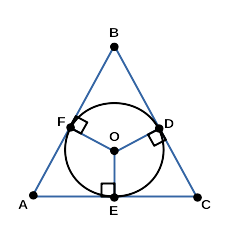
△ ABC — треугольник, описанный около окружности;
A, B, C — вершины треугольника, описанного около окружности;
F, D, E — точки касания треугольника, описанного около окружности;
O — центр окружности, вписанной в треугольник;
OD = OF = OE — радиусы треугольника, описанного около окружности;
AB, BC, CA — касательные;
FA = AE, EC = CD, FB = BD — отрезки касательных;
OF ⟂ AB, OD ⟂ BC, OE ⟂ AC;
Треугольник ABC имеет три точки, где соприкасаются
стороны и сама окружность, эти точки называют точками
касания. У данного треугольника их всего три.
В любой треугольник можно вписать окружность, причем
только одну. Треугольник, в который вписана окружность
называется треугольником описанным около окружности.
Треугольники, описанные около окружности, обладают рядом
рядом отличительных свойств, характерных признаков, уникальными
терминами, а также формулам, по которым можно найти разные величины.
Формулы радиуса вписанной окружности, радиуса описанной окружности,
диаметра, средней линии, периметра, площади стороны позволяют выразить
одни величины через другие, рассчитать длину величины, узнать во сколько
раз одна величина отличается от другой, какая прослеживается взаимосвязь.
Длина любой величины произвольного
треугольника может измеряется в мм, см, м, км.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности треугольника, описанного около окружности.
Радиус описанной окружности около треугольника
R — радиус описанной окружности треугольника, описанного около окружности.
Площадь треугольника
S — площадь треугольника, описанного около окружности.
\[ S = \frac<1><2>ab \cdot \sin \angle C \]
Периметр треугольника
P — периметр треугольника, описанного около окружности.
Сторона треугольника
a — сторона треугольника, описанного около окружности.
Средняя линия треугольника
l — средняя линия треугольника, описанного около окружности.
Высота треугольника
h — высота треугольника, описанного около окружности.
\[ h = b \cdot \sin \alpha \]
Свойства
Свойства треугольника, описанного около окружности,
а также окружности, вписанной в треугольник, медиан,
высот, биссектрис, радиусов-перпендикуляров.
Свойство 1. Окружность, можно вписать
в любой треугольник, только один раз.
Свойство 2. Центр окружности, вписанной в треугольник —
точка пересечения биссектрис, центр окружности.
Свойство 3. Центр окружности, описанной около треугольника —
точка пересечения серединных перпендикуляров.
Свойство 4. Центры вписанной и описанной окружностей
равностороннего треугольника, описанного около
окружности совпадают, имеют одну общую точку.
Свойство 5. Отрезок, проведенный из центра треугольника,
описанного около окружности, к любой из сторон,
является радиусом.
Свойство 6. У любого треугольника центр
вписанной окружности находится только внутри.
Свойство 7. Окружность находящаяся внутри
треугольника, описанного около окружности,
касается всех его сторон.
Свойство 8. Вписанная окружность и треугольник,
описанный около окружности, имеют три общие точки,
которые лежат на трех сторонах треугольника.
Свойство 9. Формула радиуса вписанной окружности
у треугольника, описанного около окружности, и четырехугольника,
у которого суммы противоположных равны, совпадает.
Свойство 10. Радиус описанной около треугольника окружности,
можно выразить и рассчитать через Теорему Синусов.
Свойство 11. У треугольника, описанного около
окружности, радиус вписанной окружности, можно
рассчитать через площадь и полупериметр.
Свойство 12. Радиус в точку касания есть перпендикуляр.
Свойство 13. Окружность, вписанная в треугольник, разделяет
стороны треугольника на 3 пары равных отрезков.
Свойство 14. Стороны треугольника, описанного около
окружности, можно также называть касательными.
Свойство 15. Отрезки, которые проведены из центра вписанной
окружности, к точкам касания, перпендикулярны сторонам.
Свойство 16. Сумма углов треугольника, описанного
около окружности, равна 180 градусам.
Свойство 17. Центр вписанной окружности
равноудален от всех сторон треугольника.
Свойство 18. Центр вписанной в треугольник окружности в научных
кругах называется замечательной точкой треугольника, либо инцентром.
Свойство 19. Правильный треугольник, описанный около
окружности, имеет точки касания с окружность, в серединах сторон.
Свойство 20. Равнобедренный, прямоугольный, равносторонний
треугольники, описанные около окружности, в точке пересечения
биссектрис и центре окружности, имеют одну общую точку.
Признаки существования
Признак 1. Центр вписанной окружности —
это точка пересечения биссектрис.
Признак 2. На сторонах треугольника лежат
три точки касания вписанной окружности.
Признак 3. Вписанная окружность делит смежные
стороны треугольника на равные отрезки касательных.
Признак 4. У вписанной окружности три радиуса в точку касания быть перпендикулярами.
Исходя из вышеперечисленных признаков, исходных
данных, внешнего вида, можно определить является ли
треугольник описанным около окружности или же нет.
Признаки равенства
Признак 1. По двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника, описанного
около окружности, равны двум сторонам и углу между ними другого
треугольника, описанного около окружности, то такие треугольники равны.
Признак 2. По стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника, описанного
около окружности, равны стороне и двум прилежащим к ней углам другого
треугольника, описанного около окружности, то такие треугольники равны.
Признак 3. По трем сторонам.
Если три стороны одного треугольника, описанного
около окружности, равны трем сторонам другого
треугольника, описанного около окружности.
Как мы знаем, любой треугольник может быть описан около
окружности, исходя из этого можно сказать, что около
окружности, могут быть описаны следующие виды треугольников:
Характерные признаки: один из углов прямой,
длину сторон можно найти через Теорему
Пифагора, сумма острых углов 90 градусов.
Основные формулы:
Характерные признаки: два угла равны,
две стороны равны, третий угол можно
найти зная два других.
Основные формулы:
Основные формулы:
Термины
Точка касания — это точка, где соприкасается вписанная
окружность с треугольником; это общая точка, для окружности
и треугольника, которая лежит на любой из сторон треугольника.
Инцентр — это точка, где пересекаются три биссектрисы
треугольника; это центр вписанной окружности в треугольник;
это одна из замечательных точек в геометрии.
Касательная — это сторона треугольника, которая имеет с
вписанной окружностью одну общую точку — точку касания.
Ортоцентр — точка, где пересекаются высоты треугольника.
Ось симметрии — это прямая, которая делит
треугольник на равные половины.
Замечательная точка — это точка пересечения медиан,
высот, биссектрис, серединных перпендикуляров.
Отрезок касательной — это отрезок, который берет начало
у одной из вершин треугольника, и имеет конец в точке касания.
Теорема синусов
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Вспомним свойство вписанного в окружность четырёхугольника:
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
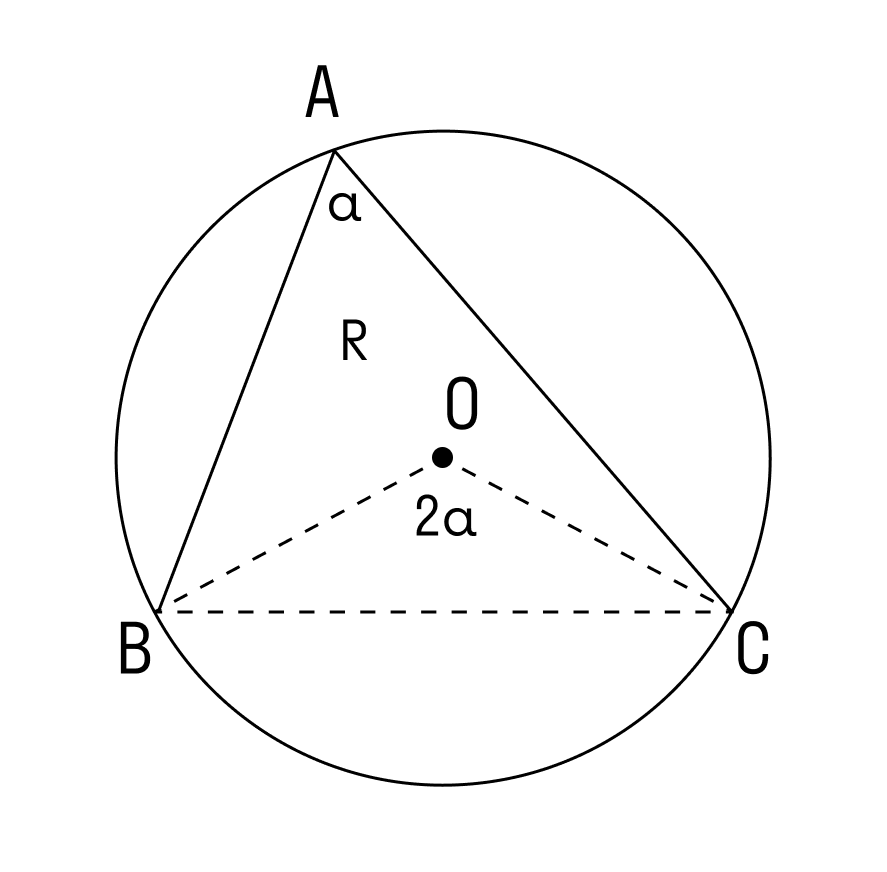
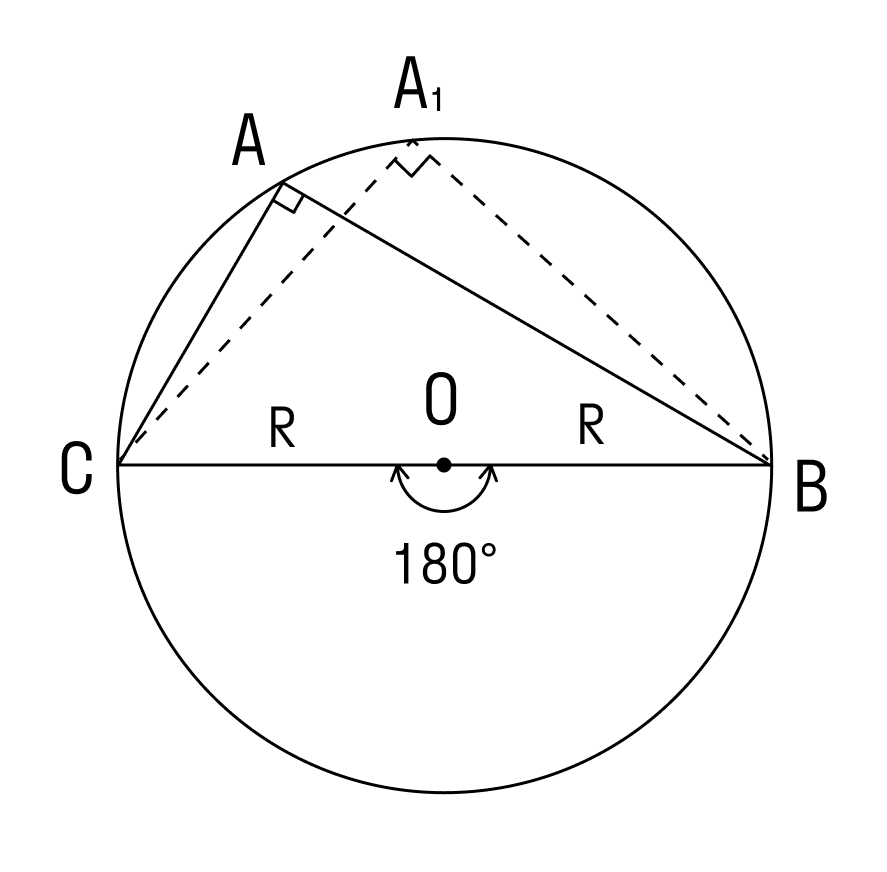
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>