Как называют объекты составляющие множество

Объекты, составляющие множество, называются его элементами.

Введение

Математика – одна из самых древних наук. Она возникла в связи с человеческой потребностью в количественном отображении окружающего мира.

Статус самостоятельной науки математика приобрела в Древней Греции примерно в четвертом веке до нашей эры. В третьем веке до нашей эры в «Началах» Евклида она выделилась в самостоятельную науку из философии. Более 2000 лет математику изучали по этой книге. И только семнадцатый век дал толчок к эволюции этой древней науки: она стала применяться Кеплером и Галилеем в астрономии, труды Декарта, Ньютона и Лейбница ввели понятие переменной величины – стал возможен переход от текстового описания к математической модели. Начинается период дифференциации математики в отдельные самостоятельные науки: алгебра, математический анализ, аналитическая геометрия. Данные преобразования и открытия привели к интенсивному развитию физики и астрономии. Язык математики стал универсальным. Математика стала использоваться и используется по сегодняшний день, не только как теоретическая наука, но и как прикладная наука в различных научных и производственных сферах.

Множества.

Множество – это одно из основных понятий математики. Синонимами этого слова являются совокупность, семейство, система.

Основателем теории множеств является немецкий математик Г. Кантор, который в 1872 году дал такое определение множества:

«Множество – это объединение в одно целое объектов, хорошо различимых нашей интуицией и мыслью»

В современной транскрипции множество – это совокупность объектов, объединенных по определенному признаку.

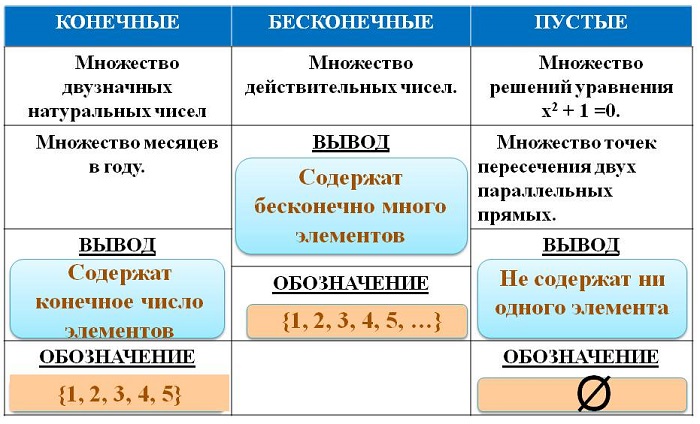
Множество может содержать конечное и бесконечное число объектов.

Объекты, составляющие множество, называются его элементами.

Множества обозначают заглавными буквами, а его элементы – соответствующими малыми: Х – множество, х – элемент множества Х. Для экономичной записи используют некоторые обозначения:

— принадлежность элемента множеству,

— непринадлежность элемента множеству,

— принадлежность одного множества другому,

— знак объединения или суммы

— знак пересечения или умножения

— знак бесконечности

— отсюда следует

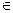
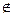
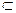
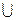
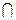
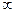
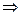
Ø – знак пустого множества

Для двух множеств определены следующие отношения:

Множество Х называется подмножеством множества У, если все элементы Х содержатся в У.
Множество, которое не содержит ни одного элемента, называется пустым множеством – Ø.

Пустое множество является подмножеством любого множества.

Источник

Что такое множество в математике и как оно обозначается

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A₁, A₂ и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a₁, a₂ и т. д.

Границы совокупности обозначаются фигурными скобками < >.

А = <а, в, с, у>– А состоит из четырех элементов.

Записать совокупность Z согласных букв в слове «калькулятор»:

Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример: N = , а Є N – элемент «а» принадлежит N.

Выделяют три вида множеств:

пустые (обозначаются Ø) – не имеющие элементов.

Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.

Если множества состоят из одинаковых элементов, их называют равными.

Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.

В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.

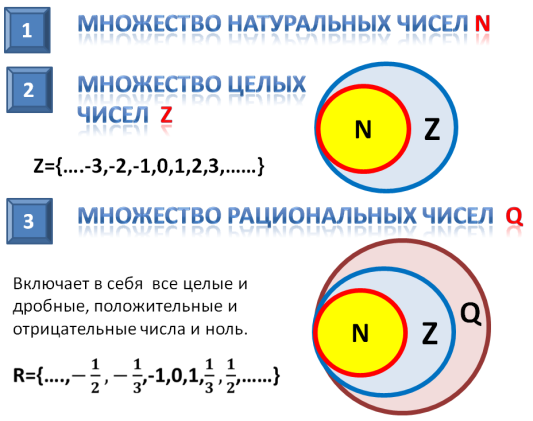
Множество натуральных чисел

Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:

Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:

Следовательно, N и Z являются подмножествами Q.

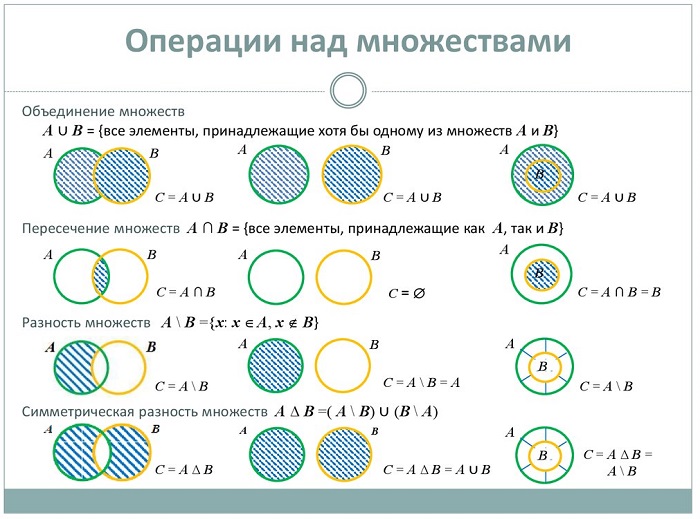
Операции над множествами

Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.

Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.

Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.

Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.

В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.

Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:

Объединение

Пересечение

Дополнение

С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.

Свойства операций над множествами

Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:

Коммутативность – переместительные законы:

умножения S ∩ D = D ∩ S;

сложения S ∪ D = D ∪ S.

Ассоциативность – сочетательные законы:

умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);

сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).

Дистрибутивность – законы распределения:

умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);

умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);

сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).

если S ⊆ Fи F ⊆ J, то S ⊆ J;

если S ⊆ F и F ⊆ S, то S = F.

Идемпотентность объединения и пересечения:

О других свойствах операций можно узнать из картинки:

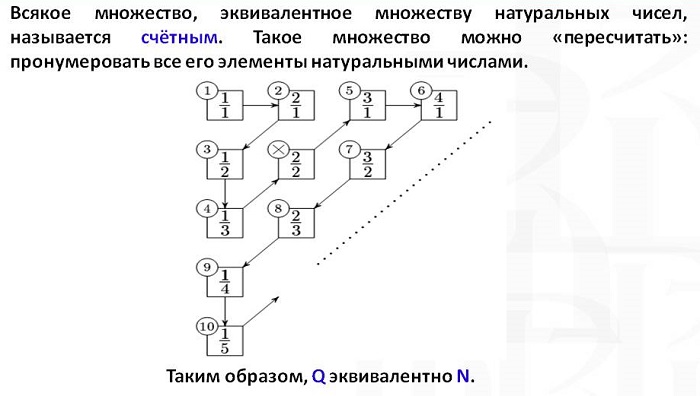
Счетные и несчетные множества

Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.

Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.

Источник

1.1.1. Элементы теории множеств. 1. Множества и операции над ними. 1. Основные понятия

Понятие Множества, как и некоторые другие исходные понятия в математике, не определяется. Ему дается описание, которое иллюстрируется примерами.

Под множеством в математике понимается любая совокупность каких-либо объектов. При этом сами объекты, составляющие множество, называются Элементами Множества. Например, можно говорить о множестве яблок в мешке, множестве натуральных чисел, множестве геометрических фигур на плоскости и т. д. Как правило, множество объединяет однотипные элементы (яблоки, числа и т. д.). Но это – не обязательно. Можно рассматривать множества, состоящие из разнородных элементов.

Если B не является элементом множества B, то пишут: .

1. М1 — множество действительных чисел R.

2. М2 — множество решений уравнения.

4. М4 — футбольная команда «Динамо-Минск» (т. е., множество футболистов этой команды).

5. М5 — множество всех футбольных команд высшей лиги.

6. М6 — множество русских слов из словаря В. И. Даля.

7. М7 — множество равносторонних треугольников.

8. М8 — множество равноугольных треугольников.

Множество B называется подмножеством множества A, если всякий элемент множества B принадлежит множеству A. В этом случае пишут: .

Множества A и B называются Равными, если их элементы совпадают.

Легко видеть, что равенство множеств Имеет место тогда и только тогда, когда и . Именно в проверке последних двух условий заключается основной способ доказательства равенства двух множеств.

Если , но , то B называется Собственным подмножеством множества A, и это записывается: .

Множества могут быть конечными и бесконечными. Число элементов конечного множества A называется его Мощностью И обозначается .

Множество мощности 0, т. е. не содержащее никаких элементов, называется Пустым Множеством И обозначается: Æ. Принято считать, что пустое множество является подмножеством любого множества A, поскольку невозможно указать ни одного элемента Æ, который бы не принадлежал множеству A. Нетрудно видеть, что справедлива

Лемма. Пустое множество единственно.

Доказательство. Действительно, если Æ1, Æ2 — два пустых множества, то согласно вышеотмеченному свойству пустого множества (быть подмножеством любого множества) имеем: и , откуда .

Источник

§1. Множества и операции над ними

Объяснение и обоснование

В курсах алгебры и алгебры и начал математического анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.

Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество М состоит из чисел 1; 2; 3, то его обозначают так: М = <1; 2; 3>. Тот факт, что число 2 входит в это множество (является элементом данного множества М), записывается с помощью специального значка ∈ следующим образом: 2 ∈ М; а то, что число 5 не входит в это множество (не является элементом данного множества), записывается так: 5 ∉ М.

Можно рассматривать также множество, не содержащее ни одного элемента, — пустое множество.

Например: множество простых делителей числа 1 — пустое множество.

Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом ∅, множество всех натуральных чисел — буквой N, множество всех целых чисел — буквой Z, множество всех рациональных чисел — буквой Q, а множество всех действительных чисел — буквой R.

Множества бывают конечными и бесконечными в зависимости от того, какое количество элементов они содержат. Так, множества А = <7>и M = <1; 2; 3>— конечные, потому что содержат конечное число элементов, а множества N, Z, Q, R — бесконечные.

Множества задают или с помощью перечисления их элементов (это можно сделать только для конечных множеств), или с помощью описания, когда задается правило (характеристическое свойство), которое позволяет определить, принадлежит или нет данный объект рассматриваемому множеству. Например, А = <–1; 0; 1>(множество задано перечислением элементов), B — множество всех четных целых чисел (множество задано характеристическим свойством всех элементов множества). Последнее множество иногда записывают так: B = или так: B = ∈ Z> — здесь после вертикальной черточки записано характеристическое свойство*.

В общем виде запись множества с помощью характеристического свойства можно обозначить так: A = , где P (x) — характеристическое свойство. Например, = < –1, 1>, ∈ R и x2 + 1 = 0> = ∅.

Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества.

Из приведенного определения равенства множеств следует, что в множестве одинаковые элементы не различаются. Действительно, например, <1; 2; 2>= <1; 2>, поскольку каждый элемент первого множества (1 или 2) является элементом второго множества и, наоборот, каждый элемент второго множества (1 или 2) является элементом первого. Поэтому, записывая множество, чаще всего каждый его элемент записывают только один раз.

Если каждый элемент множества A является элементом множества B, то говорят, что множество A является подмножеством множества B.

Это записывают следующим образом: A ⊂ B.

Например, <1; 2>⊂ <0; 1; 2; 3>, N ⊂ Z (поскольку любое натуральное число — целое), Z ⊂ Q (поскольку любое целое число — рациональное), Q ⊂ R (поскольку любое рациональное число — действительное).

Полагают, что всегда ∅ ⊆ A, то есть пустое множество является подмножеством любого множества.

Иногда вместо записи A ⊂ B используется также запись A ⊆ B.

Сопоставим определение равенства множеств с определением подмножества. Если множества А и В равны, то: 1) каждый элемент множества А является элементом множества В, следовательно, А — подмножество В (A ⊆ B); 2) каждый элемент множества В является элементом множества А, следовательно, В — подмножество А (B ⊆ A). Таким образом,

два множества равны тогда и только тогда, когда каждое из них является подмножеством другого.

Иногда соотношения между множествами удобно иллюстрировать с помощью кругов (которые часто называют кругами Эйлера–Венна). Например, рисунок 1 иллюстрирует определение подмножества, а рисунок 2 — отношения между множествами N, Z, Q, R.

Источник

Как называют объекты составляющие множество

Ключевые слова конспекта: множества, операции над множествами, подмножество, пересечение множеств, объединение множеств, элемент множества, числовые множества, обозначение некоторых числовых множеств.

В жизни часто приходится встречаться с различными совокупностями объектов, объединёнными в одно целое по некоторому признаку. Для обозначения этих совокупностей используются различные слова. Например, говорят: «стадо коров», «букет цветов», «команда футболистов» и т. д.

В математике в целях единообразия для обозначения совокупностей употребляется единый термин — множество. Например, говорят: множество чётных чисел, множество двузначных чисел, множество правильных дробей со знаменателем 5.

Термин «множество» употребляется и тогда, когда речь идёт о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек координатной плоскости, о множестве прямых, проходящих через данную точку.

Объекты или предметы, составляющие множество, называют элементами множества. Например, число 89 — элемент мнoжества двузначных чисел; точка В — элемент мнoжества вершин многоугольника ABCDE.

Множeства бывают конечные и бесконечные. Например, множество двузначных чисел — конечное множество (оно содержит 90 элементов), а множество чётных чисел — бесконечное множество.

Конечное мнoжество может содержать миллиард элементов, 2 элемента, 1 элемент или даже не содержать ни одного элемента.

Пустое множeство — это мнoжество, не содержащее ни одного элемента. Для обозначения пустого мнoжества ввели специальный знак ∅.

Конечные множeства обычно записывают с помощью фигурных скобок. Например, множество вершин пятиугольника ABCDE можно записать так: , а множество двузначных чисел, кратных 15, так: . В таких случаях говорят, что множество задано перечислением его элементов.

Множeства принято обозначать большими буквами латинского алфавита. Например, рассмотренные выше множества вершин пятиугольника и двузначных чисел, кратных 15, можно обозначить соответственно буквами К и L и записать так: К = <А, В, С, D, Е>; L = <15, 30, 45, 60, 75, 90>.

Для основных числовых множеств введены специальные обозначения: множество натуральных чисел обозначают буквой N (от латинского слова natural — «естественный»), множество целых чисел — буквой Z (от немецкого слова zahl — «число»), множество рациональных чисел — буквой Q (от латинского слова quotient — «отношение»).

В тех случаях, когда задание множества перечислением элементов невозможно (как для бесконечного множества) или громоздко (как для конечного мнoжества с большим числом элементов), множество задают описанием, указав его характеристическое свойство, т. е. свойство, которым обладают все элементы этого множeства и не обладают никакие другие объекты.

Это конспект по математике на тему «Множества. Операции над множествами». Выберите дальнейшие действия:

Источник