Как называется уравнение четвертой степени

Уравнение четвертой степени

Уравнение четвёртой степени — в математике алгебраическое уравнение вида:

.

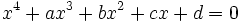
Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).

Содержание

Решения

Решение Декарта — Эйлера

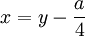
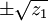
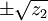
Сделав подстановку , получим уравнение в следующем виде (он называется «неполным»):

в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:

,

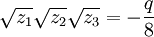
Решение Феррари

Представим уравнение четвёртой степени в виде:

Его решение может быть найдено из следующих выражений:

См. также

Литература

Ссылки

Полезное

Смотреть что такое «Уравнение четвертой степени» в других словарях:

уравнение четвертой степени — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN quartic equation … Справочник технического переводчика

Уравнение четвёртой степени — График многочлена 4 ой степени с четырьмя корнями и тремя критическими точками. Уравнение четвёртой степени в математике алгебраическое уравнение вида: Четвёртая степень для алгебраических уравнений является наивысшей, при которой… … Википедия

БИКВАДРАТНОЕ УРАВНЕНИЕ — в котором неизвестный член в четвертой степени. Полный словарь иностранных слов, вошедших в употребление в русском языке. Попов М., 1907. БИКВАДРАТНОЕ УРАВНЕНИЕ от лат. bis, дважды, и quadratum, квадрат. Уравнение, в котором наибольшая степень… … Словарь иностранных слов русского языка

Алгебра — вместе с арифметикой есть наука о числах и через посредство чисел о величинах вообще. Не занимаясь изучением свойств каких нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин как таковых, независимо от… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ПОЛЕТА ТЕОРИЯ И ПРАКТИКА — совокупность прикладных знаний, позволяющих авиационным инженерам на занятий в области аэродинамики, проблем прочности, двигателестроения и динамики полета летательных аппаратов (т.е. теории) создать новый летательный аппарат или улучшить… … Энциклопедия Кольера

МАТЕМАТИКИ ИСТОРИЯ — Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом… … Энциклопедия Кольера

Важнейшие открытия в физике — История технологий По периодам и регионам: Неолитическая революция Древние технологии Египта Наука и технологии древней Индии Наука и технологии древнего Китая Технологии Древней Греции Технологии Древнего Рима Технологии исламского мира… … Википедия

УРАВНЕНИЯ — Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида… … Энциклопедия Кольера

Теорема Абеля — Теорема Абеля Руффини утверждает, что общее уравнение степени при неразрешимо в радикалах. Содержание 1 Подробности … Википедия

Источник

В математика, а уравнение четвертой степени тот, который можно выразить как функция четвертой степени равняется нулю. Общий вид уравнения четвертой степени:

В квартика является полиномиальным уравнением высшего порядка, которое может быть решено с помощью радикалы в общем случае (т.е. такой, где коэффициенты могут принимать любые значения).

Содержание

История

Лодовико Феррари приписывается открытию решения квартики в 1540 году, но поскольку это решение, как и все алгебраические решения квартики, требует решения кубический быть найденным, его нельзя было опубликовать немедленно.[1] Решение квартики было опубликовано вместе с решением кубической наставником Феррари. Джероламо Кардано в книге Арс Магна (1545).

Доказательство того, что это был общий многочлен высшего порядка, для которого могут быть найдены такие решения, было впервые дано в Теорема Абеля – Руффини в 1824 г., доказав, что все попытки решить полиномы более высокого порядка будут тщетными. Заметки, оставленные Эварист Галуа перед смертью на дуэли в 1832 году позже привел к элегантному полная теория корней многочленов, одним из результатов которых была эта теорема. [1]

Приложения

Полиномы высоких степеней часто встречаются в задачах, связанных с оптимизация, а иногда эти многочлены оказываются квартиками, но это совпадение.

Четвертины часто возникают в компьютерной графике и во время трассировка лучей против поверхностей, таких как квадрики или же тори поверхности, которые являются следующим уровнем за пределами сфера и складывающиеся поверхности.[2]

В автоматическое производство, то тор это обычная форма, связанная с концевая фреза резак. Чтобы вычислить его положение относительно триангулированной поверхности, положение горизонтального тора на оси Z должно быть найдено там, где он касается фиксированной линии, а это требует вычисления решения общего уравнения четвертой степени. Более 10% вычислительного времени в системе CAM может быть затрачено на простое вычисление решения миллионов уравнений четвертой степени.

Программа, демонстрирующая различные аналитические решения квартики, была предоставлена ​​в Графика Самоцветы Книга V.[3]Однако ни один из трех реализованных алгоритмов не является безусловно стабильным. В обновленной версии статьи[4], который сравнивает 3 алгоритма из исходной статьи и 2 других, демонстрируется, что вычислительно устойчивые решения существуют только для 4 из возможных 16 знаковых комбинаций коэффициентов четвертой степени.

Решение уравнения четвертой степени

Особые случаи

Вырожденный случай

Если а₄ (постоянный член) = 0, то один из корней равен Икс = 0, а остальные корни можно найти делением на Икс, и решая полученный кубическое уравнение,

Биквадратные уравнения

Уравнение четвертой степени, где а₃ и а₁ равны 0, принимает вид

и таким образом биквадратное уравнение, которую легко решить: пусть z = Икс 2 < Displaystyle г = х ^ <2>> , поэтому наше уравнение превращается в

которое представляет собой простое квадратное уравнение, решения которого легко найти с помощью формулы корней квадратного уравнения:

Когда мы ее решили (т.е. нашли эти два z значения), мы можем извлечь Икс от них

Квазисимметричные уравнения

2) Используйте изменение переменной z = Икс + м/Икс.

Общий случай в духе Феррари

Для начала нужно сначала преобразовать квартику в депрессивная квартика.

Преобразование в депрессивную квартику

— общее уравнение квартики, которое требуется решить. Разделите обе стороны на А,

Первым шагом должно быть устранение Икс 3 срок. Для этого замените переменные из Икс к ты, так что

Расширение возможностей биномов дает

Собирая те же силы ты дает

Теперь переименуйте коэффициенты при ты. Позволять

В результате получается уравнение

который является депрессивное уравнение четвертой степени.

Решение Ferrari

В противном случае депрессивная квартика может быть решена с помощью метода, открытого Лодовико Феррари. После получения депрессивной квартики следующим шагом будет добавление действительного идентификатора

уравнению (1), что дает

Эти две формулы, сложенные вместе, дают

которое добавлено к уравнению (2) дает

Теперь цель состоит в том, чтобы выбрать значение для у так что правая часть уравнения (3) становится полным квадратом. Это можно сделать, позволив дискриминанту квадратичной функции стать равным нулю. Чтобы объяснить это, сначала разверните полный квадрат так, чтобы он равнялся квадратичной функции:

Квадратичная функция в правой части имеет три коэффициента. Можно проверить, что возведение второго коэффициента в квадрат с последующим четырехкратным вычитанием произведения первого и третьего коэффициентов дает ноль:

Следовательно, чтобы преобразовать правую часть уравнения (3) в полный квадрат, необходимо решить следующее уравнение:

Умножьте двучлен на многочлен,

Это кубическое уравнение за у. Разделите обе стороны на 2,

Преобразование вложенной кубики в депрессивную.

Уравнение (4) принимает вид

Расширьте возможности биномов,

Распространяйте, собирайте как силы v, и отмените пару v 2 термины,

Это угнетенное кубическое уравнение.

Обозначьте его коэффициенты,

Угнетенная кубическая теперь

Решение вложенной депрессивной кубики

Решения (подойдет любое решение, поэтому выберите любой из трех комплексных корней) уравнения (5) вычисляются как (см. Кубическое уравнение)

U = − Q 2 ± Q 2 4 + п 3 27 3 < displaystyle U = < sqrt [<3>] <- pm < sqrt <over 4> +

over 27>>> >>>

Складывание второго идеального квадрата

Со значением для у заданное уравнением (6), теперь известно, что правая часть уравнения (3) представляет собой полный квадрат вида

( s 2 ) ты 2 + ( 2 s т ) ты + ( т 2 ) = ( ( ( s 2 ) ) ты + ( 2 s т ) 2 ( s 2 ) ) 2 < displaystyle (s ^ <2>) u ^ <2>+ (2st) u + (t ^ <2>) = left ( left (< sqrt <(s ^ <2>)>> right) u + <(2st) over 2 < sqrt <(s ^ <2>)>>> right) ^ <2>> (Это верно для обоих знаков квадратного корня, если один и тот же знак используется для обоих квадратных корней. A ± является избыточным, так как он будет поглощен другим ± несколькими уравнениями ниже на этой странице.)

чтобы его можно было сложить:

Следовательно, уравнение (3) принимает вид

Уравнение (7) имеет пару свернутых полных квадратов, по одному с каждой стороны уравнения. Два идеальных квадрата уравновешивают друг друга.

Если два квадрата равны, тогда стороны двух квадратов также равны, как показано:

Собирать как силы ты производит

Уравнение (8) представляет собой квадратное уровненеие за ты. Его решение

Это решение депрессивной квартики, поэтому решения исходного уравнения квартики равны

Краткое изложение метода Феррари

Учитывая уравнение четвертой степени

ее решение можно найти с помощью следующих расчетов:

В противном случае продолжайте с

(подойдет любой знак квадратного корня)

(есть 3 сложных корня, подойдет любой из них)

который уже был в подавленном состоянии.У него есть пара решений, которые можно найти с помощью набора формул, показанного выше.

Решение Феррари в частном случае действительных коэффициентов

Если коэффициенты уравнения четвертой степени действительны, тогда вложенное депрессивное кубическое уравнение (5) также имеет действительные коэффициенты, таким образом, оно имеет по крайней мере один действительный корень.

где P и Q задаются формулой (5), обладает такими свойствами, что

Получение альтернативных решений трудным путем

но это уравнение четвертой степени эквивалентно произведению двух квадратных уравнений:

( Икс − Икс 1 ) ( Икс − Икс 2 ) = 0 ( 9 ) < Displaystyle (х-х_ <1>) (х-х_ <2>) = 0 qquad qquad (9)>

( Икс − Икс 3 ) ( Икс − Икс 4 ) = 0. ( 10 ) < Displaystyle (х-х_ <3>) (х-х_ <4>) = 0. qquad qquad (10)>

так что уравнение (9) принимает вид

Также пусть будут (неизвестные) переменные ш и v такое, что уравнение (10) принимает вид

Умножение уравнений (11) и (12) дает

Сравнивая уравнение (13) с исходным уравнением квартики, можно увидеть, что

Уравнение (12) можно решить относительно Икс уступающий

Одно из этих двух решений должно быть желаемым реальным решением.

Альтернативные методы

Быстрое и запоминающееся решение из первых принципов

Большинство хрестоматийных решений уравнения четвертой степени требуют волшебной подстановки, которую почти невозможно запомнить. Вот способ подойти к нему, чтобы его было легко понять.

Работа будет выполнена, если мы сможем разложить уравнение четвертой степени на произведение двух квадратики. Позволять

Приравнивая коэффициенты, получается следующая система одновременных уравнений:

Если мы установим п = п 2 < Displaystyle P = p ^ <2>> , то это уравнение превращается в кубическое уравнение:

Теория Галуа и факторизация

В симметричная группа S₄ по четырем элементам Кляйн четыре группы как нормальная подгруппа. Это предполагает использование резольвенты, корни которой можно по-разному описать как дискретное преобразование Фурье или Матрица Адамара преобразование корней. р_я за я от 0 до 3 являются корнями

Если теперь установить

что, если мы сделаем упрощающее предположение, что б = 0, равно

Поэтому мы можем решить квартику, решив относительно w, а затем решив корни двух множителей, используя формулу корней квадратного уравнения.

Источник

Алгебраические уравнения и способы их решения. Уравнения третьей и четвертой степени

Что делать, если вам – например, на Профильном ЕГЭ по математике – встретилось не квадратное уравнение, а кубическое? Или даже уравнение четвертой степени? Ведь для уравнений третьей, четвертой и более высоких степеней нет таких простых формул, как для квадратного уравнения.

В этой статье – способы решения сложных алгебраических уравнений. Замена переменной, использование симметрии и даже деление многочлена на многочлен.

Вспомним основные понятия.

Корень уравнения – такое число, которое мы можем подставить вместо переменной в уравнение и получить истинное равенство.

Например, число 3 – корень уравнения 2x = 6.

Решить уравнение – значит найти его корни или доказать, что их нет.

Равносильными называются уравнения, множества решений которых совпадают. Другими словами, у них одни и те же корни.

Например, уравнения и равносильны. Их корни совпадают: или

Замена переменной – ключ к решению многих задач.

Если приводить обе части к одному знаменателю, получим уравнение четвертой степени. Вряд ли мы с ним справимся.

Сделаем замену Тогда

С новой переменной уравнение стало проще:

Умножим обе части на 10t. Получим квадратное уравнение:

Корни этого уравнения: или

Вернемся к переменной

Дискриминант этого уравнения отрицателен, корней нет.

У этого уравнения два корня: или Это ответ.

Не будем спешить раскрывать скобки. Ведь раскрыв их, мы получили бы уравнение четвертной степени.

Посмотрим на уравнение внимательно.

На координатной прямой точки 1; 3; –5; –7 расположены симметрично относительно точки

Мы выразили все «скобки», то есть все множители, через новую переменную. Вот что это дает:

Обычное квадратное уравнение. Замечательно!

Подберем его корни по теореме Виета. Заметим, что

Дальше – еще интереснее.

3. Решите уравнение

Получили квадратное уравнение:

Следующее уравнение решим с помощью группировки слагаемых.

4. Решите уравнение

Разложим левую часть уравнения на множители. Сгруппируем слагаемые:

Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.

Записывается это так:

Такой знак означает «или».

Запись читается как « или или ».

Решая уравнения и особенно неравенства, мы будем постоянно пользоваться знаками системы и совокупности. Мы записываем решения в виде цепочки равносильных переходов. Для сложных уравнений и неравенств это единственный способ прийти к ответу и не запутаться.

5. Решите уравнение

Разложить левую часть на множители с первой попытки не удается.

Оказывается, если уравнение третьей (четвертой, пятой…) степени имеет целые корни, то находятся они среди делителей свободного члена (слагаемого, не содержащего x). В данном случае – среди целых делителей числа 24.

Выпишем целые делители числа 24:

1; –1; 2; –2; 3; –3; 4; –4; 6; –6; 8; –8; 12; –12; 24; –24

Подставляя их по очереди в уравнение, при получаем верное равенство:

Это значит, что левую часть уравнения можно разложить на множители:

Немного непривычно, да? Потренируйтесь – у вас получится!

6. Решите уравнение

7. Решите уравнение

Такое уравнение называется симметрическим.

Источник

Уравнения высших степеней

Вид уравнений высших степеней

Уравнения высших степеней имеют вид:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

\(a_0\) является старшим коэффициентом, который никогда не равен 0.

\(a_n \) — свободный член.

В таких уравнениях степень больше 2.

Чтобы решить уравнение высшей степени надо найти его корни, или обнаружить, что их нет. Корни представляют собой все значения переменной х, которые приводят многочлен к нулю или верному равенству.

Виды уравнений высших степеней:

На сегодняшний день в математике нет общих формул, которые бы подходили для решения уравнений высших степеней разных видов. Существуют различные системы для решения разных видов таких уравнений.

Методы решения уравнений высших степеней подразделяются на: стандартные и специальные.

Теорема Виета

Теорема Виета применяется для решения приведенных квадратных уравнений.

Первый коэффициент в таких уравнениях равен единице.

Правило теоремы Виета: Если \(x_1\) и \(x_2\) — корни приведенного квадратного уравнения \( x^2+px+q=0,\) то

Чтобы решить уравнения высших степеней по данной системе, их сначала приводят к квадратным уравнениям.

Теорема Безу

Теорема Безу — остаток при делении многочлена \(Р(х)\) на линейный многочлен \(х-α\) будет равен \(Р(α):\)

Пусть \(α\) — корень уравнения \(Р(х)=0.\)

Тогда при замене вместо х на α, получим

Это означает, что остаток при делении \( Р(х)\) на \(х-α\) :

Таким образом, данный метод решения уравнения высших степеней предполагает, что мы подбираем корень α.

В соответствии с теоремой Безу, остаток \(q\) при делении многочлена на \(х-α\) будет равен нулю, и мы получим уравнение уже на порядок ниже.

То есть, если корень подходит, то деление будет осуществляться нацело.

Как подобрать корень

Правило 1

Если \(a_0=1, \) \(a_i\in Z, \forall i.\)

Такое уравнение называется приведенным, когда старшая степень входит с коэффициентом, равным единице. Если уравнение приведенное, и \(α\) — целый корень, то \(α\) содержится в множестве делителей свободного члена:

Корень уравнения находится среди делителей свободного члена \(a_n.\)

Правило 2

В этом случае необязательно, что корень будет лежать среди делителей свободного члена. Корень может быть нецелым. Если α рациональна, то корень содержится среди дробей вида, где в числителе стоят делители свободного члена, а в знаменателе стоят делители старшего коэффициента:

Схема Горнера

По данной схеме корень уравнения находят через делители свободного члена. Метод заключается в составлении таблицы, в которой отображаются в верхней строке все коэффициенты уравнения. А в первый столбик заносятся потенциальные варианты решения, то есть делители свободного члена.

Принцип заполнения таблицы:

Такая таблица позволяет не только проверять, является ли число корнем этого уравнения, но и параллельно осуществляет деление.

Метод Феррари для уравнений 4-ой степени

Метод Феррари позволяет решить уравнения четвертой степени через их приведение к кубическому виду. Далее они решаются по формуле Кардано. То есть используется алгоритм решения кубических уравнений.

Находят \(y_0\) — любой из корней кубического уравнения:

Затем решают два квадратных уравнения:

Полный квадрат является подкоренным выражением.

Корни этих уравнений являются корнями исходного уравнения четвертой степени.

Примеры применения способов на практике

Решение заданий с помощью теоремы Безу

Рассмотрим два многочлена:

В нашем примере число \(α = 1.\)

Тогда многочлен примет вид:

Решение заданий при помощи схемы Горнера

Сначала выписываем делители свободного члена:

В первый столбец запишем единицу. Она просто носится по строкам.

Чтобы записать ответ во второй строке третьего столбца, умножим единицу на минус единицу и прибавим минус 4:

Источник

Формула решения уравнения 4 степени

Существует несколько методов нахождения корней полиномиального уравнения 4-ой степени.
Однако они не очень удобны при решении уравнений с коэффициентами, которые представляют собой выражения с параметрами.

1. Формула решения уравнения 4 степени

Рассмотрим уравнение 4-ой степени, сумма корней которого равна нулю. Коэффициенты могут быть вещественными или комплексными.

Произведение следующих двух квадратов тождественно рассматриваемому уравнению 4-ой степени.

Значение R является решением следующего кубического уравнения.

Почти такое же уравнение появляется при решении уравнения 4-ой степени путем разложения на разность полных квадратов. Будем называть данное кубическое уравнение вспомогательным.

Вычислим произведение двух квадратов new.

То же самое, но в форме коэффициентов при степенях x (в порядке убывания степеней).

Упростим выражения для коэффициентов при второй и первой степени x.

Приведенное выражение для первой степени x.

В итоге получаем k1.

Приведенное выражение для второй степени x.

Подставив выражение для R^3 получим

Итак, new тождественно уравнению 4-ой степени, сумма корней которого равна нулю.

Осталась проблема со вспомогательным кубическим уравнением.
Конечно можно использовать традиционные методы решения. Но тогда потребуется преобразовывать уравнение к каноническому виду и отдельно рассматривать три варианта решения в зависимости от значений коэффициентов. Для коэффициентов представляющих из себя выражения с параметрами это не всегда удобно.

2. Решение кубического уравнения методом преобразования Чирнгаузена

Рассмотрим решение кубического уравнения не очень широко распространенным методом преобразования Чирнгаузена.

Итак, решаем исходное уравнение

Суть метода заключается в следующих преобразованиях.

1. Вводится уравнение для y

2. Обе части равенства из п.1 умножаются на x

Затем выражение для x^3 заменяется на

В общем описанные в п.2 преобразования не являются тождественными. Но если считать интересными только значения x, которые являются корнями исходного уравнения, то данные преобразования можно считать квазитождественными. И тогда y представляется выражением, соответствующим корням исходного уравнения.

3. Для кубического уравнения операция в п.2 производится еще один раз. В итоге получается система из 3 уравнений по x, которая имеет три ненулевых решения, соответствующих корням исходного уравнения. Из коэффициентов x формируем матрицу

4. Находим определитель матрицы, который представляется кубическим выражением по y.
Вычисляем значения, обеспечивающие равенство определителя нулю.

5. В уравнении по y имеются два параметра P и Q. Вычислим их так, чтобы нулю равнялись коэффициенты при второй и первой степени y.

6. В итоге имеем уравнение c тремя кратными корнями для y

7. Остается решить квадратное уравнение с известными y, P, Q

Одно из решений будет решением исходного уравнения.

3. Параметры решения вспомогательного кубического уравнения

Для конкретных значений коэффициентов все выглядит не таким страшным образом.

Отметим, что для формулы решения уравнения 4-ой степени требуется только один корень R вспомогательного кубического уравнения.

Для конкретных коэффициентов вспомогательного уравнения имеем

При использовании формулы решения уравнения 4-ой степени необходимо ссылаться — «Метод ftvmetrics».

Интересные задачи присылайте в Direct Инстаграмм.

Источник