Как называется дробная часть числа

Дробная часть числа

Свойства функции

Источник

М. К. Потапов,В. В. Алескандров, П. И. Пасиченко Алгебра и начала анализа. — АО Столетие, 1996.

Смотреть что такое «Дробная часть числа» в других словарях:

дробная часть — числа х, разность между этим числом и его целой частью [х], то есть х = х – [х]; всегда 0≤ <х>… Энциклопедический словарь

ДРОБНАЯ ЧАСТЬ — числа х разность между этим числом и его целой частью: <х>= х [х]; всегда 0= Большой энциклопедический политехнический словарь

ДРОБНАЯ ЧАСТЬ — числа х, разность между этим числом и его целой частью [х], т. е. <х>= х [х]; всегда 0 Естествознание. Энциклопедический словарь

Целая часть числа — График целой части В математике, целая часть, антье (фр. entier) или функция «пол» (англ. floor) это функция, определённая на множестве вещественных чисел и принимающая целочисленные значения. Целая часть числа x обычно обозначается через или [x] … Википедия

Целая часть числа — см. Дробная и целая части числа … Большая советская энциклопедия

Числа с плавающей запятой — Плавающая запятая форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее… … Википедия

Числа с плавающей точкой — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… … Википедия

Целая часть — График функции «пол» (целая часть числа) … Википедия

Источник

Целая и дробная части числа

Разделы: Математика

Цели урока: познакомить учащихся с понятием целой и дробной части числа; сформулировать и доказать некоторые свойства целой части числа; познакомить учащихся с широким спектром применения целой и дробной части числа; совершенствовать умение решать уравнения и системы уравнений, содержащих целую и дробную части числа.

Оборудование: плакат “Кто смолоду делает и думает сам, тот и становится потом надёжнее, крепче, умнее” (В. Шукшин).
Проектор, магнитная доска, справочник по алгебре.

I. Организационный момент: сообщение темы урока; постановка цели урока; сообщение этапов урока.

II. Проверка домашнего задания.

Ответить на вопросы учащихся по домашнему заданию. Решить задачи, вызвавшие затруднения при выполнении домашней работы.

III. Изучение нового материала.

Во многих задачах алгебры приходится рассматривать наибольшее целое число, не превосходящее данного числа. Такое целое число получило специальное название “целая часть числа”.

Целой частью действительного числа х называется наибольшее целое число, не превосходящее х. Целая часть числа х обозначается символом [x] или Е(х) (от французского Entier “антье” ─ “целый”). Например, [5] = 5, [ π ] = 3,

Из определения следует, что [x] ≤ х, так как целая часть не превосходит х.

С другой стороны, т.к. [x] – наибольшее целое число, удовлетворяющее неравенству, то [x] +1>х. Таким образом, [x] есть целое число, определяющееся неравенствами [x] ≤ х α = υ ─ [x] называют дробной частью числа х и обозначают <х>. Тогда имеем: 0 ≤ <х>0 ≤ α о [x+у] = [x] + [у].

Это свойство распространяется на любое конечное число слагаемых:

Умение находить целую часть величины очень важно в приближенных вычислениях. В самом деле, если мы умеем находить целую часть величины х, то, приняв [x] или [x]+1 за приближенное значение величины х, мы сделаем погрешность, величина которой не больше единицы, так как

Поскольку х – целое число, то остается проверить значения от 0 до 6. Решениями уравнения оказываются числа 0,4 и 5.

Задача 7. Решить систему уравнение

(Провести проверку с помощью проектора.)

Найти число корней уравнения

Преобразуем, неравенство к виду , откуда получим, что искомое количество целых чисел равно 5. Значит, число корней данного уравнения равно 5.

Задача 9. (Соросовская олимпиада).

а) провести проверку самостоятельных работ с помощью проектора;

б) ответить на вопросы:

в) выставление отметок.

VI. Домашнее задание.

Дополнительная задача (по желанию).

Некто измерил длину и ширину прямоугольника. Он умножил целую часть длины на целую часть ширины и получил 48; умножил целую часть длины на дробную часть ширины и получил 3,2; умножил дробную часть длины на целую часть ширины и получил 1,5. Определите площадь прямоугольника.

Источник

Обыкновенные дроби

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доля целого

Доля — это каждая равная часть, из суммы которых состоит целый предмет.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:

Понятие дроби

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

Виды дробей:

Какие еще бывают дроби:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.

Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90

Полученные числа запишем справа сверху над числителем.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

Источник

Дроби обыкновенные правильные и неправильные, смешанные и составные.

Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата: обыкновенные вида и десятичные.

Числитель дроби — число, показывающее количество взятых долей (находится в верхней части дроби – над чертой). Знаменатель дроби — число, показывающее, на сколько долей разделена единица (находится под чертой – в нижней части). Обыкновенные дроби, в свою очередь делятся на: правильные и неправильные, смешанные и составные. Обыкновенные дроби тесно связаны с единицами измерения. 1 метр содержит в себе 100 см. Что означает, что 1 м разделён на 100 равных долей. Таким образом, 1 см = 1/100 м (один сантиметр равен одной сотой метра).

или 3/5 (три пятых), здесь 3 — числитель, 5 — знаменатель. Если числитель меньше знаменателя, то дробь меньше единицы и называется правильной:

Если числитель равен знаменателю, дробь равна единице. Если числитель больше знаменателя, дробь больше единицы. В обоих последних случаях дробь называется неправильной:

Чтобы выделить наибольшее целое число, содержащееся в неправильной дроби, нужно разделить числитель на знаменатель. Если деление выполняется без остатка, то взятая неправильная дробь равна частному:

Если деление выполняется с остатком, то (неполное) частное дает искомое целое число, остаток же становится числителем дробной части; знаменатель дробной части остается прежним.

Число, содержащее целую и дробную части, называется смешанным. Дробная часть смешанного числа может быть и неправильной дробью. Тогда можно из дробной части выделить наибольшее целое число и представить смешанное число в таком виде, чтобы дробная часть стала правильной дробью (или вовсе исчезла).

К подобному виду обычно и приводят смешанные дроби.

Составные дроби.

Многоэтажной, или составной дробью является дробь, которая содержит в себе несколько горизонтальных (либо реже — наклонных) черт:

либо либо .

Источник

Функция дробная часть числа

Дробной частью действительного числа называется разность между этим числом и его целой частью.

Дробную часть числа x обозначают .

По определению, =x-[x].

В частности, если n — целое число (n∈Ζ), =0.

Вычислить дробную часть числа x, если x принимает значения:

Функцию, ставящую в соответствие каждому значению x дробную часть этого числа — число , называют функцией дробной части числа и обозначают y=.

Функция дробная часть числа определена на множестве действительных чисел: x∈R.

Область значений функции — полуинтервал y∈[0;1).

По определению дробной части числа =x+k-[x+k].

По свойству целой части числа [x+k]=[x]+k.

Что и требовалось доказать.

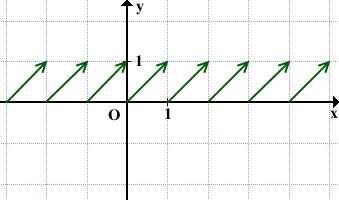
Из утверждения следует, что на каждом промежутке вида [k; k+1), где k∈Z, график функции y= имеет одинаковый вид.

То есть при x∈ [0; 1) y=x.

Стрелки на графике показывают, что правые концы отрезков не принадлежат графику.

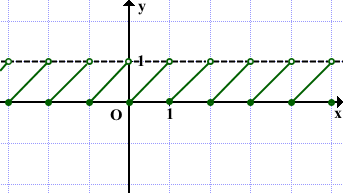
Другой вариант показать, что левые концы отрезков принадлежат графику, а правые — не принадлежат, изобразить их, соответственно, закрашенными и выколотыми точками.

Поскольку = , функция дробная часть числа является периодической. Её период T=k — любое целое число, отличное от нуля.

Наименьший положительный период (главный период) T=1.

Источник