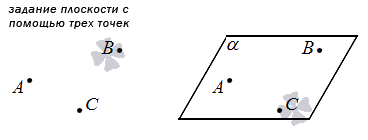Как назвать плоскость в геометрии

Плоскость в пространстве – необходимые сведения

Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.

Понятие плоскости и ее обозначения

Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.

В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.

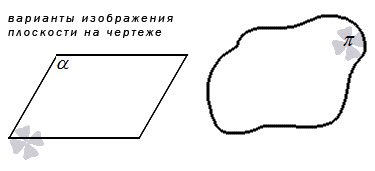
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.

Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.

Как могут располагаться плоскость и точка друг относительно друга

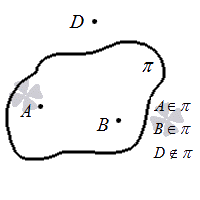
Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:

В любой плоскости есть точки.

Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.

Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.

Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:

Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.

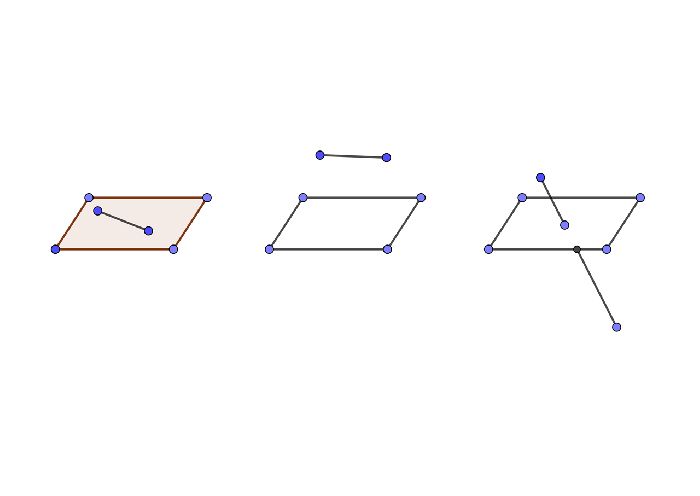
Графически последнюю аксиому можно представить так:

Варианты взаимного расположения прямой и плоскости

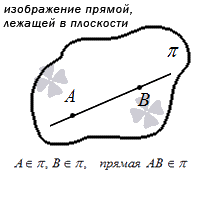
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:

Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.

Графически этот вариант расположения выглядит так:

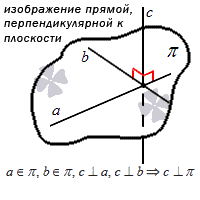
Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.

Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.

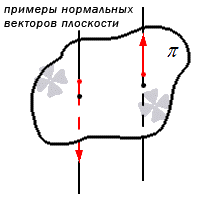
Примеры нормальных векторов плоскости показаны на рисунке:

Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.

Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.

Варианты расположения двух плоскостей друг относительно друга

1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.

2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:

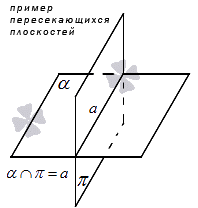
Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.

На графике это будет выглядеть так:

В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.

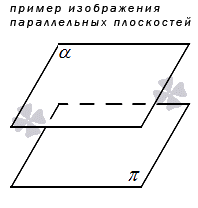
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.

Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.

Как задать плоскость в пространстве

В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.

1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.

Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:

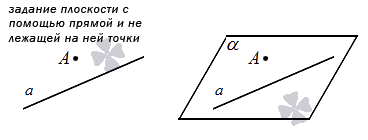
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:

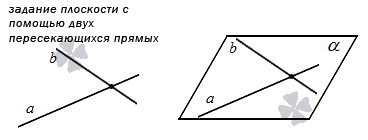
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:

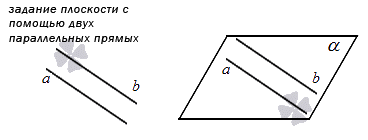
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.

На рисунке этот способ будет выглядеть так:

Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:

Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.

Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).

Вспомним одну теорему, изученную в рамках курса по геометрии:

Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.

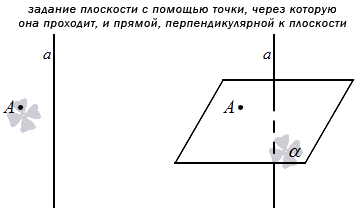
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.

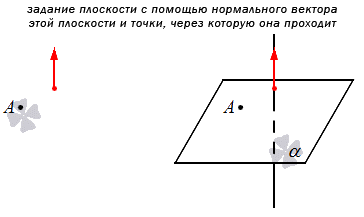
Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.

Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.

Источник

Плоскость

Всего получено оценок: 106.

Всего получено оценок: 106.

Плоскость – это основная единица планиметрии. Для правильного восприятия сложных фигур, таких как, пирамида, конус или призма, необходимо понимать и, главное, представлять себе, что такое плоскость.

Определение плоскости

Плоскость представляет поверхность, содержащую прямые, соединяющие две любые ее точки. Это определение звучит достаточно запутанно, поэтому лучше его запомнить. А для понимания стоит запомнить, что плоскость это прямая поверхность. Любая грань пирамиды это плоскость, так же как стена, поверхность стола или лист бумаги.

Стена является частью плоскости, так как любой другой пример плоскости из реальной жизни это ограниченное пространство, а плоскость безгранична, так же как и линия.

Из плоскостей в планиметрии составляются фигуры, как в стереометрии из линий. Яркий пример: четырехугольная пирамида, которая состоит из пяти граней, каждая из которых является частью отдельной плоскости.

Геометрия состоит из двух разделов: планиметрия и стереометрия. Фигуры на плоскости, состоящие из линий и точек это раздел стереометрии. Планиметрия изучает фигуры из плоскостей, прямых и точек. Проще говоря, планиметрия – это геометрия объемных фигур.

Способы задания плоскостей

Плоскость может быть задана тремя точками, нележащими на одной прямой. Из этого утверждения следуют еще два варианта задания плоскостей. При этом специального знака плоскостей не существует.

Плоскость можно задать двумя пересекающимися прямыми, тогда одной точкой будет служить точка пересечения прямых, а двумя другими произвольные точки на одной и второй прямой.

Еще один вид это задание прямой и точкой, нележащей на этой прямой. По аналогии со вторым вариантам: одна точка уже есть и не лежит на прямой, а две других это произвольные точки имеющейся линии.

Рис. 1. Способы задания плоскостей.

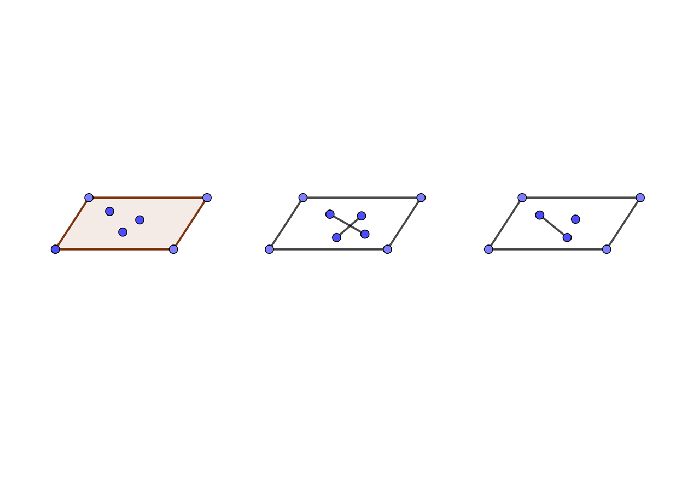
Взаимное расположение прямой и плоскости

Прямая в пространстве может быть параллельной плоскости, лежать в плоскости и пересекать ее. Рассмотрим каждый вариант более подробно.

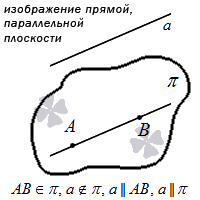
Прямая параллельная плоскости, если она не имеет общих точек с ней. Признак параллельности прямой и плоскости крайне прост: прямая параллельна плоскости, если параллельна любой прямой лежащей в этой плоскости.

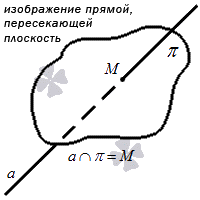
Прямая в пространстве может пересекать плоскость, если имеет с ней одну общую точку. Обратите внимание, что тогда прямая и плоскость образуют угол. Чтобы его увидеть, необходимо провести прямую в плоскости через точку пересечения. Тогда угол между этими прямыми и будет углом между прямой и плоскостью. Кроме того, прямая может быть перпендикулярна плоскости. Признак перпендикулярности прямой и плоскости звучит так: прямая перпендикулярна плоскости, если она перпендикулярна каждой из двух пересекающихся прямых в этой плоскости и пересекает плоскость в месте пересечения этих прямых.

Прямая в пространстве может лежать в плоскости, если две любые точки этой прямой принадлежат этой плоскости.

Рис. 2. Взаимное расположение прямой и плоскости.

Взаимное расположение плоскостей

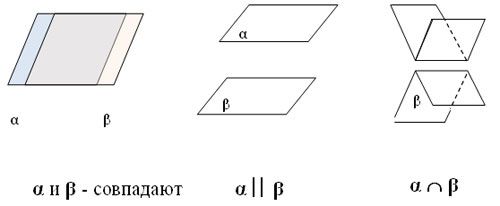
Плоскости в пространстве могут совпадать, пересекаться или быть параллельными.

Плоскости параллельны, если попарно параллельны две пересекающиеся прямые в каждой из плоскостей.

Пересекаться плоскости могут только по прямой. В этом случае плоскости образуют угол. Чтобы найти его численные значения нужно в каждой из плоскостей провести прямую перпендикулярную прямой пересечения плоскостей. Эти две прямые и образуют угол плоскостей. Эти свойства иногда называют правилами плоскостей.

Рис. 3. Расположение плоскостей.

Что мы узнали?

Мы дали определение и привели примеры плоскости. Выделили варианты пересечения прямой и плоскости и пересечения плоскостей. Привели несколько признаков, относящихся с плоскостям и разобрали все случаи существования плоскостей в пространстве.

Источник

Лекция 3. Плоскость

3.1. Способы задания плоскости на ортогональных чертежах

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный – απ₁, фронтальный – απ₂ и профильный – απ₃, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π₁, фронтальной π₂ и профильной π₃ (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

Рисунок 3.6 – Принадлежность прямой плоскости

\left.\begin\alpha=m\parallel n,\\D\in\alpha\\C\in\alpha\\\end\right\> \Longrightarrow CD\in\alpha

Упражнение

Рисунок 3.7 – Решение задачи

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π₁) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π₂) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π₃) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

\alpha=m\cap n\\\left.\begina_2\parallel m_2\\a_1\parallel m_1\\\end\right\> \Rightarrow a\parallel\alpha

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ⊥π₁. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π₁ или π₂.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π₂ (рис. 3.15)
Выберем точки, конкурирующие на π₂ – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π₂ надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π₂.
Направление взгляда на π₂ показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π₂, видно, что точка 4₁ располагается ближе к наблюдателю, чем 3₁.
4₁∈E₁F₁ ⇒ 4∈EF ⇒ на π₂ будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π₁.
Для определения видимости выберем точки, конкурирующие на π₁ – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π₁ надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π₁.
Направление взгляда на π₁ показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π₁, видно, что точка 2₂ располагается ближе к наблюдателю, чем 5₂.
2₂∈А₂В₂ ⇒ 2∈АВ ⇒ на π₁ будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Упражнение

Алгоритм решения задачи :

\left.\beginAB\cap\sigma=K\\AC\cap\sigma=L\\\end\right\> \left.\begin\Rightarrow A_1B_1\cap\sigma_1=K_1 \rightarrow K_2\\\Rightarrow A_1C_1\cap \sigma_1=L_1 \rightarrow L_2\\\end\right.

KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Упражнение

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

\left.\begin\alpha\cap\sigma=(4-5)\\\beta\cap\sigma=(3-2)\\\end\right\>\\\left.\begin\alpha\cap\tau=(6-7)\\\beta\cap\tau=(1-8)\\\end\right\>\left.\begin(4_1-5_1)\cap(3_1-2_1)=M_1\rightarrow M_2\\(6_1-7_1)\cap(1_1-8_1)=N_1\rightarrow N_2\\\end\right\>\rightarrow\\\left.\beginM_1N_1\\M_2N_2\\\end\right\>\Rightarrow\alpha\cap\beta=MN

Упражнение

Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π₂, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π₂ (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение

Задана плоскость σ⊥π₂ и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C₁D₁ должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.

Постройте фронтальную проекцию точки К.

2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π₂, если его диагональ MN //π₂ (Рисунок 3.26).

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π₁.

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π₁.

Источник