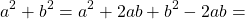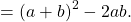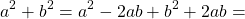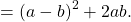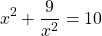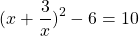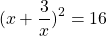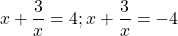Как можно разложить сумму квадратов
Сумма квадратов
Сумма квадратов встречается в ходе преобразования числовых и буквенных выражений. Как с ней работать?
Поскольку сумма квадратов является составной частью формул полного квадрата суммы и разности, можно попробовать применить одну из этих формул.
Формула полного квадрата суммы состоит из трёх слагаемых — сумма квадратов двух слагаемых плюс удвоенное произведение этих слагаемых. Следовательно, для получения полного квадрата к сумме квадратов двух выражений следует прибавить удвоенное произведение этих выражений, и, чтобы выражение не изменилось, вычесть это произведение:
Аналогично, для получения полного квадрата разности следует из суммы квадратов двух выражений вычесть удвоенное произведение этих выражений и тут же прибавить его:
Рассмотрим, как эти рассуждения могут быть применены на практике.
Теперь используем данные условия:
Эти рассуждения применяются, например, в приложении теоремы Виета, когда не решая квадратного уравнения, требуется найти сумму квадратов его корней и т.п.
Представление чисел суммой двух квадратов и эллиптические кривые
Совсем легко понять, почему 3, 7, 11 и прочие числа, дающие при делении на 4 остаток 3, непредставимы в виде a 2 +b 2 : квадрат чётного числа всегда делится на 4, квадрат нечётного числа всегда даёт остаток 1 при делении на 4, сумма двух квадратов при делении на 4 может давать остатки 0, 1 или 2, но никак не 3. Представимость простых чисел вида 4k+1 неочевидна (особенно если заметить, что простота существенна: число 21 хотя и имеет нужный остаток, но суммой двух квадратов не представляется).
Вычеты
Натуральных чисел бесконечно много. Бывает полезно объединять их в классы по каким-нибудь признакам. В частности, объединение по остатку от деления на какое-нибудь число n приводит к вычетам по модулю n: вычет x̅ — это класс всех чисел, которые при делении на n дают тот же остаток, что и x. Что эквивалентно, вычет x̅ состоит из всех чисел вида x+n∙k, где k целое. В рамках данного поста все вычеты будут по модулю p (того самого нечётного простого числа из введения). Естественно, различных вычетов столько же, сколько может быть остатков от деления на p, то есть ровно p. По сравнению с бесконечностью натуральных чисел переход к вычетам сильно сокращает число вариантов.
Операции над классами далеко не всегда имеют смысл. Например, попытка сложить класс простых чисел с классом составных чисел не очень осмысленна: мы умеем складывать только числа, а у суммы простого числа и составного числа не видно свойств, общих для класса. Хотя члены клуба тавтологии и могут сказать, что сложение класса простых чисел и класса составных чисел даёт класс чисел, раскладывающихся в сумму простого числа и составного числа.
Для вычетов, тем не менее, сложение, вычитание и умножение, «унаследованные» от натуральных чисел, дают другие вычеты. Например, 2̅+3̅=5̅: возьмём любое число с остатком 2, любое число с остатком 3, и их сумма обязательно даст остаток 5. Вообще говоря, произведение двух ненулевых вычетов по произвольному модулю может внезапно оказаться нулём, 2̅∙3̅=0̅ по модулю 6, что неприятно. Но в случае простого модуля, очевидно, такого не бывает, как говорят, нет делителей нуля. Кроме того, можно решить уравнение a̅∙x̅=b̅ (операция деления) для любых двух вычетов, кроме случая a̅=0̅, и результат будет однозначно определён. Однозначность следует из того, что произведение ненулевых вычетов ненулевое. Поскольку a̅≠0̅, то наибольший общий делитель a и p равен 1 (здесь тоже нужна простота p), расширенный алгоритм Евклида найдёт x и y такие, что a∙x+p∙y=1, откуда следует a̅∙x̅=1̅, а значит, a̅∙(b̅∙x̅)=b̅.
Важное следствие из отсутствия делителей нуля: ненулевой многочлен от одной переменной степени n не может иметь более n корней. (Это хорошо известно для обычных целых чисел, но при использовании операций над вычетами требует дополнительного обоснования: уравнение 3̅∙x̅=0̅ по модулю 6 имеет три решения 0̅, 2̅, 4̅.) Действительно, обычное деление «в столбик» показывает, что любой многочлен f(x) можно представить в виде f(x)=(x-с)g(x)+(некоторая константа), где многочлен g(x) имеет степень на единицу меньше; если c — это корень f(x), то константа равна нулю (подставим x=c); если c’ — другой корень f(x), то он будет корнем g(x) (здесь важно отсутствие делителей нуля), так что процесс можно продолжить. Если уже набралось n корней, то оставшийся g(x) будет константой, причём ненулевой (иначе f(x)=0) и больше корней не имеет.
Вычеты по простому модулю можно складывать, вычитать, умножать. На ненулевые вычеты можно делить. Все эти операции обладают обычными свойствами типа a̅∙b̅=b̅∙a̅. В умных книгах говорят, что вычеты по простому модулю образуют поле (а вычеты по составному модулю, где делить нельзя, а всё остальное такое же, — коммутативное кольцо). И не надо быть умной книгой, чтобы назвать это поле конечным. Поле вычетов — не единственное конечное поле, но другие конечные поля нам не понадобятся.
Чуть-чуть про эллиптические кривые
Квадратичные вычеты и невычеты
Теперь мы готовы предъявить обещанные формулы для компонентов разложения p в сумму двух квадратов. Теорема. Пусть g — любой квадратичный невычет. Если p при делении на 4 даёт остаток 1, то 
причём число в первой скобке целое нечётное, число во второй скобке целое чётное. Если же p при делении на 4 даёт остаток 3, то обе суммы в скобках нулевые (а значит, число точек на эллиптических кривых равно p+1).
Доказательство
Поскольку пост и без того длинный, доказательство убрано под спойлер. Его можно спокойно пропустить без ущерба для восприятия.
Если взять ненулевой вычет c и умножить его на все вычеты от 1̅ до p̅-1̅, все произведения будут ненулевыми и попарно различными (если c∙x=c∙y, то c∙(x-y)=0̅, что при ненулевом c может быть только если x=y), а значит, это будет просто какая-то перестановка всех вычетов от 1̅ до p̅-1̅. Следовательно, 1̅∙2̅∙. ∙(p̅-1̅)=(c∙1̅)∙(c∙2̅)∙. ∙(c∙(p̅-1̅))=c p-1 ∙1̅∙2̅∙. ∙(p̅-1̅) и c p-1 =1̅ для любого ненулевого вычета c. (Это было доказательство малой теоремы Ферма.)
Как следствие, получаем 
Если p даёт остаток 1 при делении на 4, то слагаемые с x и -x равны и их сумма четна. Значит, вся сумма также четна и числа в скобках действительно целые. Чётность/нечётность после деления пополам ненамного сложнее: в первой скобке теоремы есть три нулевых слагаемых, остальные слагаемые разбиваются на (p-3)/2 пар с суммой ±2 в каждой паре; при любом знаке при делении на 4 получается остаток 2, вся сумма при делении на 4 даёт остаток такой же, как p-3, то есть 2. После деления пополам получим нечётное число. Во второй скобке теоремы всего одно нулевое слагаемое и (p-1)/2 пар с ±2, итоговый остаток от деления на 4 получается 0, после деления пополам остаётся чётное число.
Пусть p при делении на 4 даёт остаток 1. Обозначим первую скобку теоремы через a, вторую через b. Мы уже знаем, что a и b целые.
Итак, первый способ вычисления даёт
Если x2/x1 — квадратичный невычет, то аналогично эллиптическим кривым число решений равно 2p минус число решений в случае квадратичного вычета, то есть 2p-(p-1)=p+1.
Суммируем. Есть один вариант с x1=x2=0, дающий p решений. Есть 2(p-1) вариантов, где один из x нулевой, а другой ненулевой, каждый из вариантов даёт p решений. Есть 2(p-1) вариантов с x2=±x1, каждый из которых даёт 2p-1 решений. Есть (p-1)((p-1)/2-2) вариантов, где x1 — произвольный ненулевой вычет, а x2/x1 — квадратичный вычет, отличный от ±1̅, каждый из этих вариантов даёт p-1 решений. Наконец, остаётся (p-1) 2 /2 вариантов, где x1 — произвольный ненулевой вычет, а x2/x1 — квадратичный невычет, в каждом из этих вариантов p+1 решений. Итого 
Сравнение двух выражений для N завершает доказательство.
Причём здесь криптография?
Знание числа точек на кривой важно для криптографии на этой кривой. На эллиптической кривой можно ввести операцию сложения точек (о чём слышали, наверное, все, кто хоть что-то знает о криптографии) со специальной точкой O в роли нуля. На основе операции сложения можно определить умножение на натуральное число: 2P=P+P, 3P=P+P+P и так далее. Так вот, можно доказать, что если n — порядок кривой, то nP=O для любой точки P. Зная n, c, d, можно решать уравнения вида x∙(cP)=dP полностью аналогично делению вычетов: расширенный алгоритм Евклида найдёт x, y такие, что c∙x+n∙y=1, откуда x∙(cP)+y∙(nP)=P, то есть x∙(cP)=P. При этом, если c, d неизвестны, а cP и dP заданы координатами, то эффективных методов деления в общем случае неизвестно.
Вычислить число точек на заданной кривой довольно сложно (полиномиальный алгоритм существует, но на практике довольно медленный). Чтобы построить кривую с какими-нибудь свойствами на число точек, можно пытаться взять случайные коэффициенты и вычислять число точек в цикле, пока не получится то, что надо, но придётся подождать. К счастью, есть другой способ.
Суммы квадратов, суммы кубов.
Задача
Еще в древнем Египте была известна формула для суммы последовательных натуральных чисел:
Убедиться в том, что эта формула работает, можно, взяв несколько разных значений \(n\) и подставив их в формулу, а для доказательства ее истинности при всех \(n\) сложите первое слагаемое с последним, второе с предпоследним и т. д.
Найдите формулу для суммы а) квадратов \(1^2+2^2+\ldots+n^2\); б) кубов \(1^3+2^3+\ldots+n^3\); в) четвертых степеней \(1^4+2^4+\ldots+n^4\).
Подсказка 1
Начните c эксперимента: вычислите первые несколько сумм (\(1^2+2^2\), \(1^2+2^2+3^2\) и т. д. хотя бы до \(n=5\)). После этого попробуйте найти закономерность.
Подсказка 2
Экспериментальные данные полезно записать в виде таблицы:
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) |
| \(1^<\phantom1>+\ldots+n^<\phantom1>\) | \(1\) | \(3\) | \(6\) | \(10\) | \(15\) | \(21\) | \(28\) |
| \(1^2+\ldots+n^2\) | \(1\) | \(5\) | \(14\) | \(30\) | \(55\) | \(91\) | \(140\) |
| \(1^3+\ldots+n^3\) | \(1\) | \(9\) | \(36\) | \(100\) | \(225\) | \(441\) | \(784\) |
| \(1^4+\ldots+n^4\) | \(1\) | \(17\) | \(98\) | \(354\) | \(979\) | \(2275\) | \(4676\) |
Попробуйте найти связь между числами в (одном столбце, но) разных строках.
Подсказка 3
Если у чисел в двух строках постоянно появляются общие делители (например, 10 и 30 делятся на 10, 15 и 55 — на 5, 21 и 91 — на 7 и т. д.), то полезно изучить отношение этих чисел. Что за последовательности получаются? (Удобно добавить в таблицу из второй подсказки соответствующие строки.)
Решение
Как и предлагалось в последней подсказке, изучим отношение первых двух строк.
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) |
| \(S_1\) | \(1\) | \(3\) | \(6\) | \(10\) | \(15\) | \(21\) | \(28\) |
| \(S_2\) | \(1\) | \(5\) | \(14\) | \(30\) | \(55\) | \(91\) | \(140\) |
| \(S_2/S_1\) | \(1\) | \(5/3\) | \(7/3\) | \(3\) | \(11/3\) | \(13/3\) | \(5\) |
Теперь нетрудно заметить закономерность: с увеличением \(n\) на 1 частное увеличивается на \(2/3\), то есть это частное равно \((2n+1)/3\). Вместе с формулой для суммы \(1+2+\ldots+n\) это дает (гипотетический) ответ
С суммами кубов дело обстоит даже проще, чем с квадратами — глядя на таблицу естественно предположить, что \(S_3=S_1^2\), то есть
Заметно сложнее угадать формулу для суммы четвертых степеней. В отличие от предыдущих случаев, у \(S_4(n)\) практически не видно общих делителей с \(S_1(n)\) (кроме двойки). Зато можно заметить, что 14 и 98 делятся на 7, 55 и 979 — на 11. Посмотрим на отношение \(S_4/S_2\):
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(S_2\) | \(1\) | \(5\) | \(14\) | \(30\) | \(55\) | \(91\) |
| \(S_4\) | \(1\) | \(17\) | \(98\) | \(354\) | \(979\) | \(2275\) |
| \(S_4/S_2\) | \(1\) | \(17/5\) | \(7\) | \(59/5\) | \(89/5\) | \(25\) |
Видно, что после домножения этого отношения на 5 получится последовательность целых чисел: 5, 17, 35, 59, 89, 125. Тут уже нельзя сказать, что разность соседних чисел неизменна. Но если выписать эти разности: 12, 18, 24, 30. то закономерность сразу становится видной!
Таким образом, гипотеза состоит в том, что
Итак, стало понятно, какие должны быть ответы, но как их доказать?
И что вообще значит, что какое-то выражение \(P(n)\) дает формулу для суммы \(1^2+\ldots+n^2\)?
Аналогичным образом (говоря формально — по индукции) можно доказать найденные выше формулы для \(S_3(n)\) и \(S_4(n)\).
Послесловие
Геометрическое доказательство формулы для суммы \(1+2+\ldots+n\)
Видимо наиболее наглядный способ вычислить сумму \(1+2+\ldots+n\) — геометрический: об этой сумме можно думать как о треугольном числе, то есть площади «пиксельного» (составленного из единичных квадратиков) равнобедренного прямоугольного «треугольника» со стороной \(n\). Из двух таких треугольников легко составить прямоугольник размера \(n\times(n+1)\), откуда и получается ответ \(n(n+1)/2\) (половина площади прямоугольника).
Пирамидка, составленная из квадратов со стороной \(1\), \(2\), …, \(n\)
Подобным образом можно вычислить и сумму \(1^2+2^2+\ldots+n^2\): ее можно проинтерпретировать как объем пирамиды из кубиков (нижний слой которой состоит из \(n^2\) кубиков, следующий — из \((n-1)^2\) кубиков и т. д.), после чего сложить из шести таких пирамид параллелепипед \(n\times(n+1)\times(2n+1)\). Как это сделать, можно посмотреть на сайте «Математические этюды».
Есть геометрические доказательства и у позволяющего вычислить сумму кубов замечательного равенства \(1^3+2^3+\ldots+n^3=(1+2+\ldots+n)^2\). Одно из них можно посмотреть на youtube-канале Think Twice, см. также подборку «доказательств без слов» в «Кванте» №11 за 2017 год.
Заметим, однако, что формула для суммы четвертых степеней не раскладывается (в отличие от предыдущих) на простые линейные множители. Видимо из-за этого ее не получается найти методами геометрического суммирования и открыта она была примерно на 1000 лет позже, чем формула для суммы кубов (известная уже в античности).
Чтобы продвинуться дальше, полезно задуматься, что мы вообще надеемся увидеть в качестве ответа. Не любое алгебраическое выражение можно разложить на достаточно простые множители, но всегда можно, наоборот, раскрыть все скобки и привести подобные. В изученных нами случаях получаются следующие многочлены от \(n\):
Практически сразу возникает гипотеза, что вообще для любого \(k\) сумма \(1^k+2^k+\ldots+n^k\) равна многочлену от \(n\), который начинается с \(\frac1
С алгебраической точки зрения это очень естественный переход — но самого языка алгебры, «выражений с буквами» и преобразования таких выражений, не существовало до работ Франсуа Виета (конца XVI века)! А до появления такого языка описанную выше гипотезу практически невозможно не то что доказать — сформулировать.
В первой половине XVII века Иоганн Фаульхабер смог найти формулы для сумм \(1^k+2^k+\ldots+n^k\) до \(k=17\) (интересную попытку реконструкции рассуждений Фаульхабера опубликовал Дональд Кнут). Вот несколько из таких формул:
Коэффициенты при \(n^

Понимать эту запись следует следующим образом. Нужно раскрыть формально в выражении \((n+B)^
Если поверить в эту (крайне странную, на первый взгляд) процедуру, то будет ясно и как вычислять числа Бернулли: при подстановке \(n=1\) получается равенство \(1=\frac<(1+B)^
| \(m\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) | \(9\) | \(10\) | \(11\) | \(12\) | \(13\) | \(14\) |
| \(B^m\) | \(1\) | \(\frac12\) | \(\frac16\) | \(0\) | \(-\frac1<30>\) | \(0\) | \(\frac1<42>\) | \(0\) | \(-\frac1<30>\) | \(0\) | \(\frac5<66>\) | \(0\) | \(-\frac<691><2730>\) | \(0\) | \(\frac76\) |
Замечательным образом те же самые числа Бернулли возникают и в квадратурных формулах для вычисления приближенных значений интегралов, и при вычислении бесконечных сумм типа \(1+\frac14+\frac19+\frac1<16>+\ldots=\frac<\pi^2>6\) (то есть значений знаменитой дзета-функции), и в комбинаторике, и в теории чисел, и в топологии.
Литература по теме:
1) Д. Пойа. Математика и правдоподобные рассуждения (М.: Наука, 1975). — Мало где можно прочитать не о конкретной области математики, а о том, как вообще решать новую для себя математическую задачу. Подсказки и решение выше по существу следуют главе 7 этой замечательной книги.
2) Интервью с академиком И. М. Гельфандом // Квант, 1989, № 1, стр. 3–12. — В приведенном выше решении сделана попытка объяснить, как некоторые формулы для сумм степеней мог бы искать любой человек. Интересующимся математикой может быть интересно прочитать, как такую задачу решал в школьные годы один из выдающихся математиков XX века (собственно про это — небольшой фрагмент на стр. 8–9, но все интервью интересное).
3) В. С. Абрамович. Суммы одинаковых степеней натуральных чисел // Квант, 1973, № 5, стр. 22–25. — Можно прочитать доказательство формулы для суммы степеней (из конца послесловия), использующее, по сути, только бином Ньютона.
4) Г. А. Мерзон. Алгебра, геометрия и анализ сумм степеней последовательных чисел // Математическое просвещение, сер. 3, вып. 21 (2017), стр. 104–118. — Подробная статья о разных взглядах на задачу о суммировании степеней.
5) Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика (М.: Мир, 1998). — В учебнике, написанном по лекциям знаменитого Дональда Кнута, обсуждается и задача о суммировании степеней, и числа Бернулли.